华东师大版七下数学10.5图形的全等教案
文档属性
| 名称 | 华东师大版七下数学10.5图形的全等教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 00:00:00 | ||
图片预览

文档简介
§10.5 图形的全等
教学目标
【知识与技能】
1.借助具体情境和图案,经历观察、发现、实践操作和重叠图形等过程.
2.理解图形全等的意义.
3.掌握图形全等的特征.
【过程与方法】
学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣.
【情感态度】
学生积极参与图形全等的探究过程,从中体会合作与成功的快乐,建立学好数学的自信心,体会图形全等在现实生活中的应用价值.
【教学重点】全等多边形特征及应用.
【教学难点】全等多边形对应元素的识别.
教学过程
情境导入,初步认识
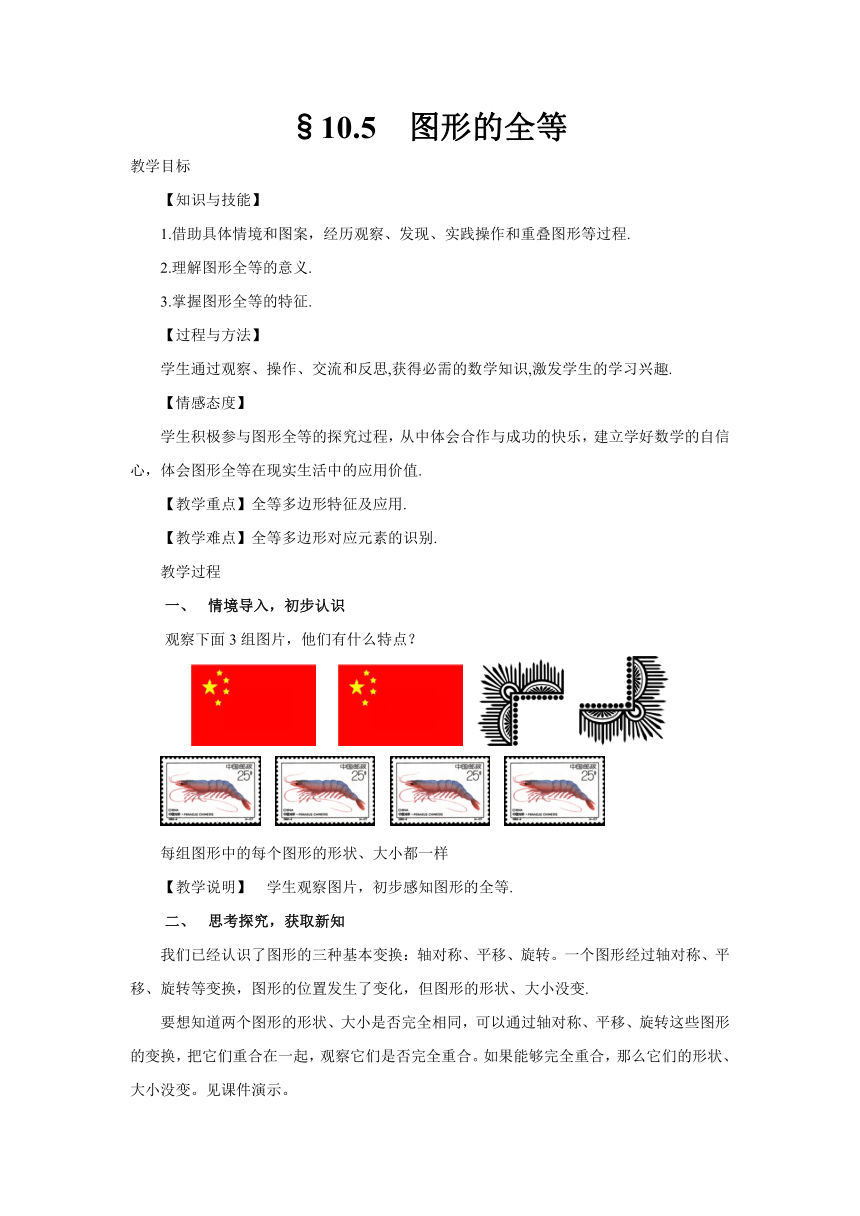
观察下面3组图片,他们有什么特点?
每组图形中的每个图形的形状、大小都一样
【教学说明】 学生观察图片,初步感知图形的全等.
思考探究,获取新知
我们已经认识了图形的三种基本变换:轴对称、平移、旋转。一个图形经过轴对称、平移、旋转等变换,图形的位置发生了变化,但图形的形状、大小没变.
要想知道两个图形的形状、大小是否完全相同,可以通过轴对称、平移、旋转这些图形的变换,把它们重合在一起,观察它们是否完全重合。如果能够完全重合,那么它们的形状、大小没变。见课件演示。
归纳总结 能够完全重合的两个图形叫做全等图形.
想一想:观察下面两组图形,它们是不是全等图形 为什么?与同伴进行交流。(见课件演示)
第一组两个图形形状相同,但大小不同;第二组两个图形面积相同,但形状不同。它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
做一做 课本P133:“做一做”
议一议 如果两个图形全等,它们的形状与大小一定相同吗?
全等图形的形状与大小都相同
归纳总结 一个图形经过轴对称、平移、旋转等变换所得到的新图形一定与原图形全等;反过来,两个全等的图形经过轴对称、平移、旋转等变换后一定能够互相重合。
思考:观察下图中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过运动而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”.).点A与A′,B与B′,C与C′,D与D′,E与E′分别是对应顶点。(见课件演示)
归纳总结 全等多边形的对应边、对应角分别相等.
边、角分别对应相等的两个多边形是全等多边形。
三角形是特殊的多边形,因此,
全等三角形的对应边、对应角分别相等.
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
练一练:见课件演示
【教学说明】 通过探究,使学生了解全等图形、全等多边形、全等三角形的概念,掌握全等图形的性质.
三、运用新知,深化理解
1、例题:教材第135页例题。(见课件演示)
2、当堂练习(见课件演示)
【教学说明】 通过练习,检测学生掌握的情况。
四、课堂小结及课后作业
1. 课堂小结
2. 布置作业:教材第136页“习题10.5”中第1、2、3题.
教学反思
通过这节课的教学实践,使学生对所学的内容兴趣盎然、乐于探究;使教师认识到教学必须紧密联系学生的生活和实际,.教师的表现应该是的引导者、组织者、合作者,而不是表演者。注意培养学生的创新意识与实践能力.
1、能够完全重合的两个图形
2、对应点、对应角、对应边
概念
1、性质:全等多边形对应边、对应角分别相等
2、判定:边、角分别对应相等的多边形是全等多边形
全等图形
全等多边形
1、性质:全等三角形对应边、对应角分别相等
2、判定:边、角分别对应相等的三角 形是全等三角形
全等三角形
教学目标
【知识与技能】
1.借助具体情境和图案,经历观察、发现、实践操作和重叠图形等过程.
2.理解图形全等的意义.
3.掌握图形全等的特征.
【过程与方法】
学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣.
【情感态度】
学生积极参与图形全等的探究过程,从中体会合作与成功的快乐,建立学好数学的自信心,体会图形全等在现实生活中的应用价值.
【教学重点】全等多边形特征及应用.
【教学难点】全等多边形对应元素的识别.
教学过程
情境导入,初步认识
观察下面3组图片,他们有什么特点?
每组图形中的每个图形的形状、大小都一样
【教学说明】 学生观察图片,初步感知图形的全等.
思考探究,获取新知
我们已经认识了图形的三种基本变换:轴对称、平移、旋转。一个图形经过轴对称、平移、旋转等变换,图形的位置发生了变化,但图形的形状、大小没变.
要想知道两个图形的形状、大小是否完全相同,可以通过轴对称、平移、旋转这些图形的变换,把它们重合在一起,观察它们是否完全重合。如果能够完全重合,那么它们的形状、大小没变。见课件演示。
归纳总结 能够完全重合的两个图形叫做全等图形.
想一想:观察下面两组图形,它们是不是全等图形 为什么?与同伴进行交流。(见课件演示)
第一组两个图形形状相同,但大小不同;第二组两个图形面积相同,但形状不同。它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
做一做 课本P133:“做一做”
议一议 如果两个图形全等,它们的形状与大小一定相同吗?
全等图形的形状与大小都相同
归纳总结 一个图形经过轴对称、平移、旋转等变换所得到的新图形一定与原图形全等;反过来,两个全等的图形经过轴对称、平移、旋转等变换后一定能够互相重合。
思考:观察下图中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过运动而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”.).点A与A′,B与B′,C与C′,D与D′,E与E′分别是对应顶点。(见课件演示)
归纳总结 全等多边形的对应边、对应角分别相等.
边、角分别对应相等的两个多边形是全等多边形。
三角形是特殊的多边形,因此,
全等三角形的对应边、对应角分别相等.
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
练一练:见课件演示
【教学说明】 通过探究,使学生了解全等图形、全等多边形、全等三角形的概念,掌握全等图形的性质.
三、运用新知,深化理解
1、例题:教材第135页例题。(见课件演示)
2、当堂练习(见课件演示)
【教学说明】 通过练习,检测学生掌握的情况。
四、课堂小结及课后作业
1. 课堂小结
2. 布置作业:教材第136页“习题10.5”中第1、2、3题.
教学反思
通过这节课的教学实践,使学生对所学的内容兴趣盎然、乐于探究;使教师认识到教学必须紧密联系学生的生活和实际,.教师的表现应该是的引导者、组织者、合作者,而不是表演者。注意培养学生的创新意识与实践能力.
1、能够完全重合的两个图形
2、对应点、对应角、对应边
概念
1、性质:全等多边形对应边、对应角分别相等
2、判定:边、角分别对应相等的多边形是全等多边形
全等图形
全等多边形
1、性质:全等三角形对应边、对应角分别相等
2、判定:边、角分别对应相等的三角 形是全等三角形
全等三角形
