人教版七年级数学下册5.2.2平行线的判定 教学设计
文档属性
| 名称 | 人教版七年级数学下册5.2.2平行线的判定 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 15:14:24 | ||
图片预览

文档简介
5.2.2平行线的判定
(第一课时)
教学目标:
1.掌握两条直线平行的判定方法。
2.了解得到两条直线平行判定方法的证明过程。
3.进一步规范学生几何推理语言的表达。
学情分析:
本课是学生在对平行线已有初步认识的基础上展开的,通过前几节课的学习,学生大多数有了一定说理能力,但由于学生的基础不同,理解能力有强弱,因此教学中要特别要加强学生的操作探究意识,以及学生验证应用能力,力争使大部分学生应用同位角、内错角、同旁内角数量的关系,来证明两直线平行。
教学重点:
掌握两条直线平行的判定方法。
教学难点:
灵活运用两条直线平行的判定方法证明直线平行。
教学方法:
实践操作法,探究归纳法,交流应用法。
教学过程:
一、回顾与思考:
教师出示问题,学生回答。
1.什么是平行线?
同一平面内,不相交的两直线叫做平行。
2,判定两条直线平行的方法有哪两种?
(1)定义:在同一平面内,不相交的两条直线叫平行线。
(2)平行公理的推论(平行线的传递性):如果两条直线同平行于一条直线,那么两条直线平行。
二、引入新课:
想一想:除应用以上两种方法以外,是否还有其它方法呢?
学生操作:过直线AB外一点P作直线AB的平行线CD,看看你能作出吗?能作出几条?
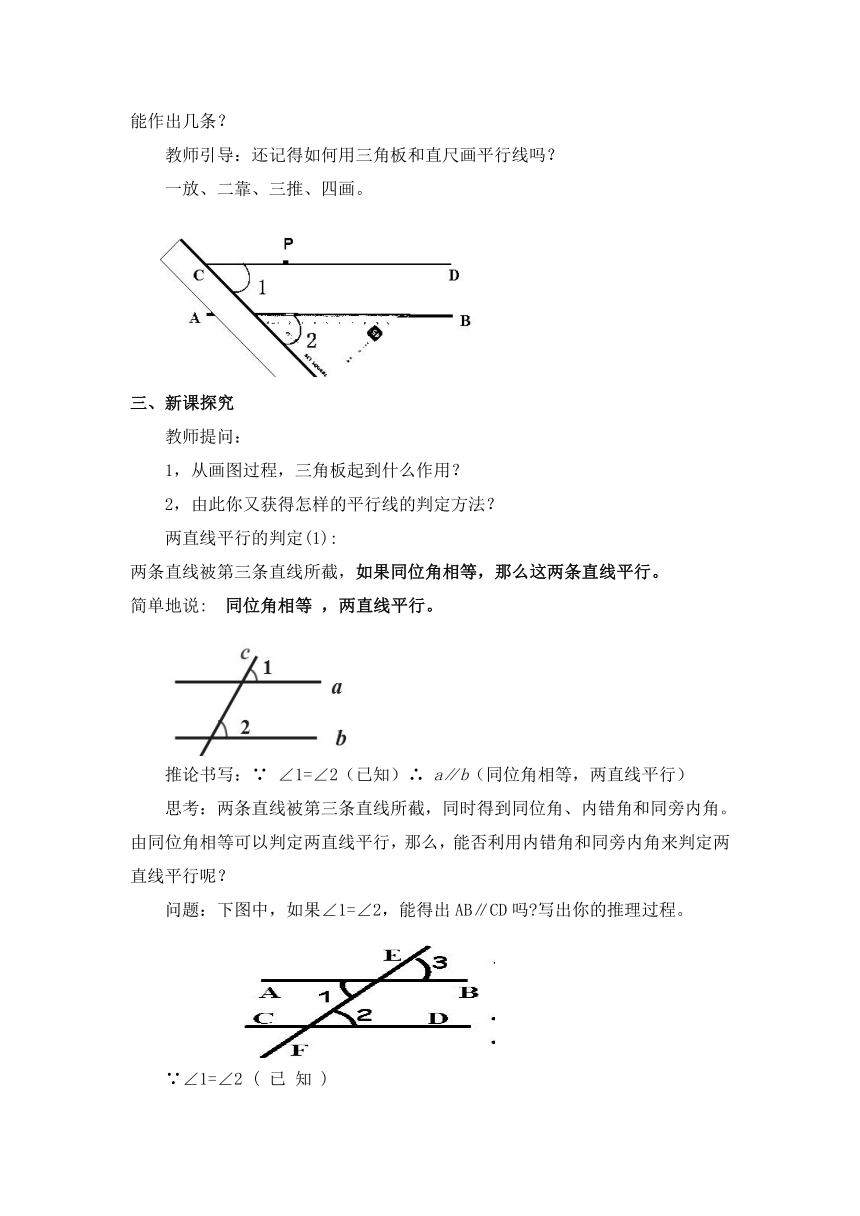
教师引导:还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
三、新课探究
教师提问:
1,从画图过程,三角板起到什么作用?
2,由此你又获得怎样的平行线的判定方法?
两直线平行的判定(1):
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说: 同位角相等 ,两直线平行。
推论书写:∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角。
由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
问题:下图中,如果∠1=∠2,能得出AB∥CD吗 写出你的推理过程。
∵∠1=∠2 ( 已 知 )
∠1=∠3( 对顶角相等 )
∴ ∠2=∠3(等量代换 )
∴ AB∥CD(同位角相等,两直线平行)
思考:由此你又获得怎样的平行线的判定方法?
两直线平行的判定(2): 两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行。
简单地说: 内错角相等 ,两直线平行。
推论书写:∵ ∠1=∠2(已知)∴ a∥b(内错角相等,两直线平行)
问题:下图中,如果∠1+∠2=180°,能得出AB∥CD 写出你的推理过程。
∵ ∠1+∠2=180 °(已知)
∠1+∠3=180°(邻补角的定义)
∴ ∠2=∠3(同角的补角相等)
∴ AB∥CD(同位角相等, 两直线平行)
思考:1.你还有其它的说理方法吗?(引导学生利用内错角相等完成)
2.由此你又获得怎样的平行线的判定方法?
两直线平行的判定(3):两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单地说:同旁内角互补,两直线平行。
推论书写:∵ ∠1+∠2=180°(已知)∴ a∥b(同旁内角互补,两直线平行)。
教师归纳总结:
如何由三类角的数量关系来判断两条直线平行?
练一练:(教师多媒体出示,学生回答)
例题:(教材14页)
问题:你还有其他方法证明吗?
教师引导学生从内错角相等和同旁内角互补来证明。
实 践 应用
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?
教师引导学生分别从同位角、内错角、同旁内角的数量关系来判断。
三、小结内容:
判定两条直线是否平行的方法有:1.同位角相等, 两直线平行。2.内错角相等, 两直线平行。3.同旁内角互补, 两直线平行。4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行。5.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
四、布置作业:课本P15页 第1、2、4、7 题。
五、板书设计:
5.2.2平行线的判定1.平行线定义及平行公理的推论。 2.两直线平行的判定(1)、(2)、(3)。3.练习(多媒体) 4.例题(教材)5.小结:两直线平行的判定方法(1)、(2)、(3)、(4)、(5)。6.布置作业:课本P15页 第1、2、4、7 题。
六、教学反思:
(第一课时)
教学目标:
1.掌握两条直线平行的判定方法。
2.了解得到两条直线平行判定方法的证明过程。
3.进一步规范学生几何推理语言的表达。
学情分析:
本课是学生在对平行线已有初步认识的基础上展开的,通过前几节课的学习,学生大多数有了一定说理能力,但由于学生的基础不同,理解能力有强弱,因此教学中要特别要加强学生的操作探究意识,以及学生验证应用能力,力争使大部分学生应用同位角、内错角、同旁内角数量的关系,来证明两直线平行。
教学重点:
掌握两条直线平行的判定方法。
教学难点:
灵活运用两条直线平行的判定方法证明直线平行。
教学方法:
实践操作法,探究归纳法,交流应用法。
教学过程:
一、回顾与思考:
教师出示问题,学生回答。
1.什么是平行线?
同一平面内,不相交的两直线叫做平行。
2,判定两条直线平行的方法有哪两种?
(1)定义:在同一平面内,不相交的两条直线叫平行线。
(2)平行公理的推论(平行线的传递性):如果两条直线同平行于一条直线,那么两条直线平行。
二、引入新课:
想一想:除应用以上两种方法以外,是否还有其它方法呢?
学生操作:过直线AB外一点P作直线AB的平行线CD,看看你能作出吗?能作出几条?
教师引导:还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
三、新课探究
教师提问:
1,从画图过程,三角板起到什么作用?
2,由此你又获得怎样的平行线的判定方法?
两直线平行的判定(1):
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说: 同位角相等 ,两直线平行。
推论书写:∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角。
由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
问题:下图中,如果∠1=∠2,能得出AB∥CD吗 写出你的推理过程。
∵∠1=∠2 ( 已 知 )
∠1=∠3( 对顶角相等 )
∴ ∠2=∠3(等量代换 )
∴ AB∥CD(同位角相等,两直线平行)
思考:由此你又获得怎样的平行线的判定方法?
两直线平行的判定(2): 两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行。
简单地说: 内错角相等 ,两直线平行。
推论书写:∵ ∠1=∠2(已知)∴ a∥b(内错角相等,两直线平行)
问题:下图中,如果∠1+∠2=180°,能得出AB∥CD 写出你的推理过程。
∵ ∠1+∠2=180 °(已知)
∠1+∠3=180°(邻补角的定义)
∴ ∠2=∠3(同角的补角相等)
∴ AB∥CD(同位角相等, 两直线平行)
思考:1.你还有其它的说理方法吗?(引导学生利用内错角相等完成)
2.由此你又获得怎样的平行线的判定方法?
两直线平行的判定(3):两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单地说:同旁内角互补,两直线平行。
推论书写:∵ ∠1+∠2=180°(已知)∴ a∥b(同旁内角互补,两直线平行)。
教师归纳总结:
如何由三类角的数量关系来判断两条直线平行?
练一练:(教师多媒体出示,学生回答)
例题:(教材14页)
问题:你还有其他方法证明吗?
教师引导学生从内错角相等和同旁内角互补来证明。
实 践 应用
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?
教师引导学生分别从同位角、内错角、同旁内角的数量关系来判断。
三、小结内容:
判定两条直线是否平行的方法有:1.同位角相等, 两直线平行。2.内错角相等, 两直线平行。3.同旁内角互补, 两直线平行。4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行。5.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
四、布置作业:课本P15页 第1、2、4、7 题。
五、板书设计:
5.2.2平行线的判定1.平行线定义及平行公理的推论。 2.两直线平行的判定(1)、(2)、(3)。3.练习(多媒体) 4.例题(教材)5.小结:两直线平行的判定方法(1)、(2)、(3)、(4)、(5)。6.布置作业:课本P15页 第1、2、4、7 题。
六、教学反思:
