17.1.3 勾股定理的几何应用 课件(共32页)
文档属性
| 名称 | 17.1.3 勾股定理的几何应用 课件(共32页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
17.1 勾股定理
人教版八下数学
第3课时 勾股定理的几何应用
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
-1 0 1 2 3
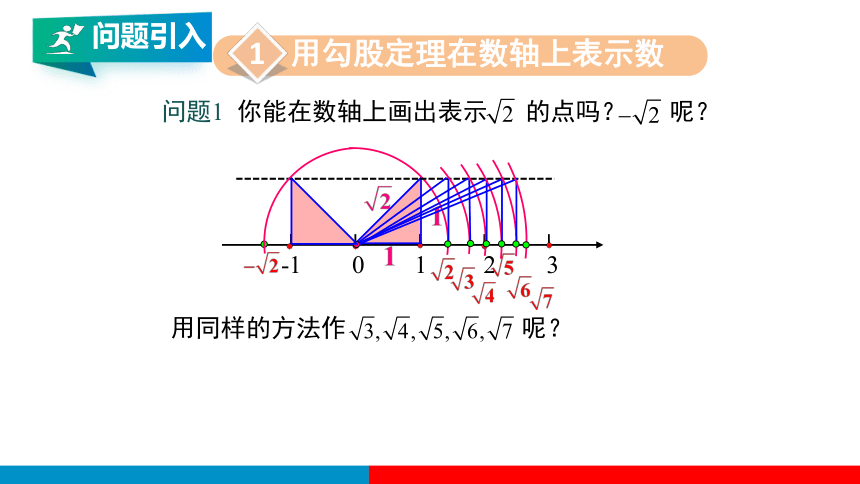
问题1 你能在数轴上画出表示 的点吗? 呢?
用同样的方法作 呢?
用勾股定理在数轴上表示数
1
问题引入
我们知道数轴上的点有的表示有理数,有的表示无理
数,你能在数轴 上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都
为1的直角三角形的斜边.长为 的线段能是直角边的长
为正整数的直角三角形的斜边吗?
问题引入
0
1
2
3
4
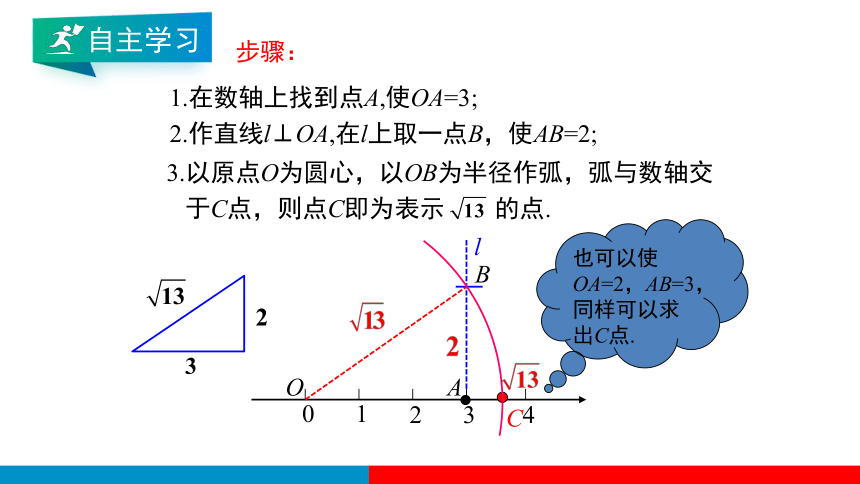
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
自主学习
自主学习
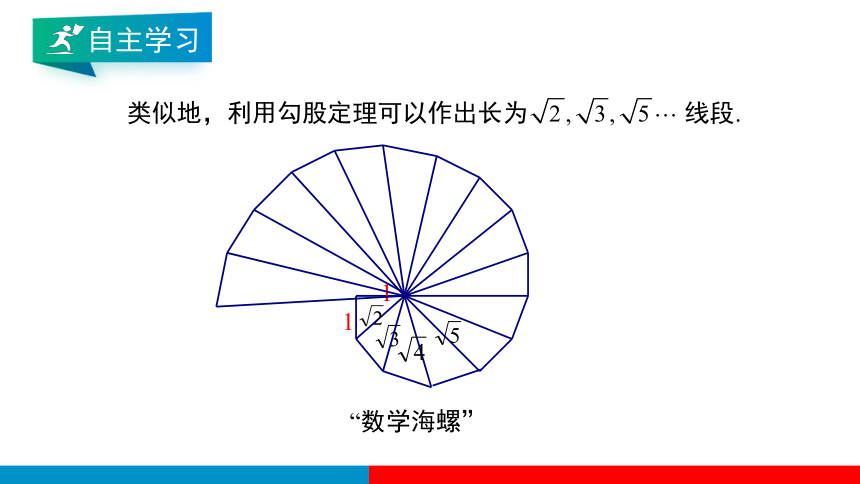
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
1
1
自主学习
例 1
如图1,已知线段AB的长为a,请作出长为 a
的段.(保留作图痕迹,不写作法)
利用 a= 可以作出.
如图2,先作出与已知线段AB垂直,
且与已知线段的端点A相交的直线l,
在直线l上以A为端点截取长为2a的线
段AC,连接BC,则线段BC即为所求.
如图2,BC就是所求作的线段.
图1
图2
导引:
解:
典例分析
总 结
这类问题要作的线段一般是直角三角形的斜
边,根据勾股定理由要作的线段确定两直角边的
长是解题的关键.
自主学习
1.
在数轴上做出表示 的点.
如图所示.作法:
(1)在数轴上找出表示4的点A,则OA=4;
(2)过A作直线l垂直于OA;
(3)在直线l上取点B,使AB=1;
(4)以原点O为圆心,以OB为半径作弧,弧与
数轴的交点C即为表示 的点.
解:
课堂练习
2.
如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
课堂练习
勾股定在几何问题中的应用
2
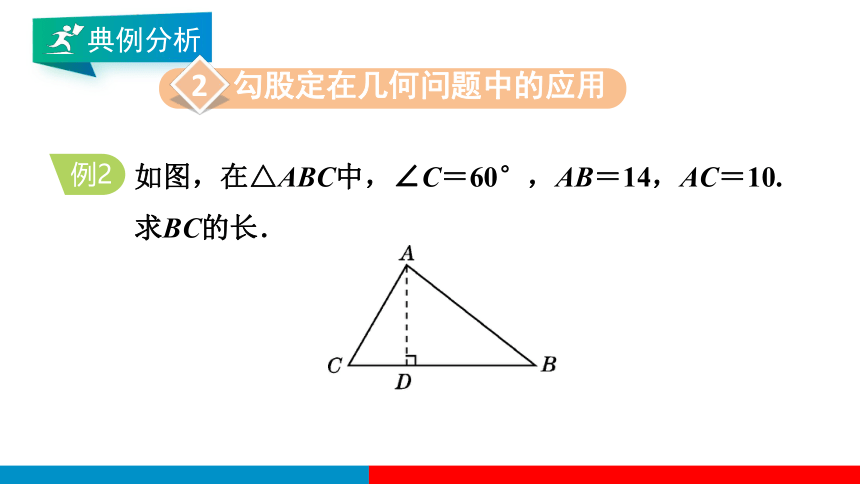
例2
如图,在△ABC中,∠C=60°,AB=14,AC=10. 求BC的长.
典例分析
思路:题中没有直角三角形,可以通过作高构建直角三角形;过点 A作AD⊥BC于D,图中会出现两个直角三角形——Rt△ACD和Rt△ABD,这两个直角三角形有一条公共边AD,借助这条公共边,可建立起直角三角形之间的联系.
典例分析
解:如图,过点A作AD⊥BC于D.
∵∠ADC=90°,∠C=60°,∴CD= AC=5.
在Rt△ACD中,
AD
在Rt△ABD中,
BD
∴BC=BD+CD=11+5=16.
典例分析
总 结
利用勾股定理求非直角三角形中线段的长的方法:
作三角形一边上的高,将其转化为两个直角三角形,然
后利用勾股定理并结合已知条件,采用推理或列方程的
方法解决问题.
1.
如图,等边三角形的边长是6.求:
(1)高AD的长;
由题意可知,在Rt△ADB中,
AB=6,BD= BC=3,∠ADB=90°.
由勾股定理,
得AD=
解:
课堂练习
(2)这个三角形的面积.
S△ABC= BC·AD= ×6×3
=
解:
课堂练习
勾股定理的几何应用
1.勾股定理与三角形三边平方关系的综合应用:
单一应用:先由三角形三边平方关系得出直角三角形后,
再求这个直角三角形的角度和面积:
综合应用:先用勾股定理求出三角形的边长,再由三角形
平方关系确定三角形的形状,进而解决其他问题;
逆向应用:如果一个三角形两条较小边长的平方和不等于
最大边长的平方,那么这个三角形就不是直角三角形.
2.应用勾股定理解题的方法:
(1)添线应用,即题中无直角三角形,可以通过作垂线,构
造直角三角形,应用勾股定理求解;
(2)借助方程应用,即题中虽有直角三角形,但已知线段的
长不完全是直角三角形的边长,可通过设未知数,构建
方程,解答计算问题;
(3)建模应用,即将实际问题建立直角三角形模型,通过勾
股定理解决实际问题.
1.在数轴上作出表示 的点.
解:∵
∴ 是以4,2为直角边长的直角三角形的斜边
长.在数轴上表示如图所示.
备选习题
在△ABC中,∠C=90°,AB=c.
(1) 如果∠A=30°,求BC,AC;
2.
解:(1) ∵AB=c,∠C=90°,∠A=30°,
∴
由勾股定理,得
备选习题
(2) 如果∠A=45°,求BC,AC.
(2) ∵AB=c,∠C=90°,∠A=45°,
∴ ∠B=45°.∴ AC=BC.
设AC=BC=x,由勾股定理,得AC2+BC2=AB2=c2.
∴2x2=c2.∴x=
∴AC=BC=
备选习题
在△ABC中,∠C=90°,AC=2.1,BC=2.8.求:
(1) △ABC的面积;
(2) 斜边AB;
3.
解:
(2) 由勾股定理,得
备选习题
(3) 高CD.
备选习题
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2. 求斜边AB的长.
4.
解:在Rt△ABC中,∵∠A=30°,
由勾股定理,得AB2=BC2+AC2.
备选习题
有5个边长为1的正方形,排列形式如图. 请把它们分割后拼接成一个大正方形.
5.
解:因为5个边长为1的正方形的面积和是5,所以拼成的大正方形的边长应为 .所以原图的分割与拼接如图所示.
备选习题
如图,分别以等腰Rt△ACD的边AD,AC,CD为直径画半圆.求证:所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.
6.
解:由题意得
备选习题
又根据勾股定理,得AC2+CD2=AD2,
∴S半圆AEC+S半圆CFD=S半圆ACD,
S阴影=S△ACD+S半圆AEC+S半圆CFD-S半圆ACD,
即S阴影=S△ACD.
备选习题
如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
求证:AE2+AD2=2AC2.(提示:连接BD)
7
证明:如图,连接BD.
∵△ECD和△ACB都为等腰直角三角形,
∴∠ECD=∠ACB=90°.
∴∠ECA=∠DCB.
备选习题
又∵CE=CD,CA=CB,
∴△ACE≌△BCD.
∴AE=BD,∠CDB=∠E=45°.
又∠EDC=45°,
∴∠ADB=90°.
在Rt△ADB中,AD2+DB2=AB2,易得AD2+AE2=AC2+CB2,
即AE2+AD2=2AC2.
备选习题
https://www.21cnjy.com/help/help_extract.php
17.1 勾股定理
人教版八下数学
第3课时 勾股定理的几何应用
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
-1 0 1 2 3
问题1 你能在数轴上画出表示 的点吗? 呢?
用同样的方法作 呢?
用勾股定理在数轴上表示数
1
问题引入
我们知道数轴上的点有的表示有理数,有的表示无理
数,你能在数轴 上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都
为1的直角三角形的斜边.长为 的线段能是直角边的长
为正整数的直角三角形的斜边吗?
问题引入
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
自主学习
自主学习
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
1
1
自主学习
例 1
如图1,已知线段AB的长为a,请作出长为 a
的段.(保留作图痕迹,不写作法)
利用 a= 可以作出.
如图2,先作出与已知线段AB垂直,
且与已知线段的端点A相交的直线l,
在直线l上以A为端点截取长为2a的线
段AC,连接BC,则线段BC即为所求.
如图2,BC就是所求作的线段.
图1
图2
导引:
解:
典例分析
总 结
这类问题要作的线段一般是直角三角形的斜
边,根据勾股定理由要作的线段确定两直角边的
长是解题的关键.
自主学习
1.
在数轴上做出表示 的点.
如图所示.作法:
(1)在数轴上找出表示4的点A,则OA=4;
(2)过A作直线l垂直于OA;
(3)在直线l上取点B,使AB=1;
(4)以原点O为圆心,以OB为半径作弧,弧与
数轴的交点C即为表示 的点.
解:
课堂练习
2.
如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
课堂练习
勾股定在几何问题中的应用
2
例2
如图,在△ABC中,∠C=60°,AB=14,AC=10. 求BC的长.
典例分析
思路:题中没有直角三角形,可以通过作高构建直角三角形;过点 A作AD⊥BC于D,图中会出现两个直角三角形——Rt△ACD和Rt△ABD,这两个直角三角形有一条公共边AD,借助这条公共边,可建立起直角三角形之间的联系.
典例分析
解:如图,过点A作AD⊥BC于D.
∵∠ADC=90°,∠C=60°,∴CD= AC=5.
在Rt△ACD中,
AD
在Rt△ABD中,
BD
∴BC=BD+CD=11+5=16.
典例分析
总 结
利用勾股定理求非直角三角形中线段的长的方法:
作三角形一边上的高,将其转化为两个直角三角形,然
后利用勾股定理并结合已知条件,采用推理或列方程的
方法解决问题.
1.
如图,等边三角形的边长是6.求:
(1)高AD的长;
由题意可知,在Rt△ADB中,
AB=6,BD= BC=3,∠ADB=90°.
由勾股定理,
得AD=
解:
课堂练习
(2)这个三角形的面积.
S△ABC= BC·AD= ×6×3
=
解:
课堂练习
勾股定理的几何应用
1.勾股定理与三角形三边平方关系的综合应用:
单一应用:先由三角形三边平方关系得出直角三角形后,
再求这个直角三角形的角度和面积:
综合应用:先用勾股定理求出三角形的边长,再由三角形
平方关系确定三角形的形状,进而解决其他问题;
逆向应用:如果一个三角形两条较小边长的平方和不等于
最大边长的平方,那么这个三角形就不是直角三角形.
2.应用勾股定理解题的方法:
(1)添线应用,即题中无直角三角形,可以通过作垂线,构
造直角三角形,应用勾股定理求解;
(2)借助方程应用,即题中虽有直角三角形,但已知线段的
长不完全是直角三角形的边长,可通过设未知数,构建
方程,解答计算问题;
(3)建模应用,即将实际问题建立直角三角形模型,通过勾
股定理解决实际问题.
1.在数轴上作出表示 的点.
解:∵
∴ 是以4,2为直角边长的直角三角形的斜边
长.在数轴上表示如图所示.
备选习题
在△ABC中,∠C=90°,AB=c.
(1) 如果∠A=30°,求BC,AC;
2.
解:(1) ∵AB=c,∠C=90°,∠A=30°,
∴
由勾股定理,得
备选习题
(2) 如果∠A=45°,求BC,AC.
(2) ∵AB=c,∠C=90°,∠A=45°,
∴ ∠B=45°.∴ AC=BC.
设AC=BC=x,由勾股定理,得AC2+BC2=AB2=c2.
∴2x2=c2.∴x=
∴AC=BC=
备选习题
在△ABC中,∠C=90°,AC=2.1,BC=2.8.求:
(1) △ABC的面积;
(2) 斜边AB;
3.
解:
(2) 由勾股定理,得
备选习题
(3) 高CD.
备选习题
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2. 求斜边AB的长.
4.
解:在Rt△ABC中,∵∠A=30°,
由勾股定理,得AB2=BC2+AC2.
备选习题
有5个边长为1的正方形,排列形式如图. 请把它们分割后拼接成一个大正方形.
5.
解:因为5个边长为1的正方形的面积和是5,所以拼成的大正方形的边长应为 .所以原图的分割与拼接如图所示.
备选习题
如图,分别以等腰Rt△ACD的边AD,AC,CD为直径画半圆.求证:所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.
6.
解:由题意得
备选习题
又根据勾股定理,得AC2+CD2=AD2,
∴S半圆AEC+S半圆CFD=S半圆ACD,
S阴影=S△ACD+S半圆AEC+S半圆CFD-S半圆ACD,
即S阴影=S△ACD.
备选习题
如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
求证:AE2+AD2=2AC2.(提示:连接BD)
7
证明:如图,连接BD.
∵△ECD和△ACB都为等腰直角三角形,
∴∠ECD=∠ACB=90°.
∴∠ECA=∠DCB.
备选习题
又∵CE=CD,CA=CB,
∴△ACE≌△BCD.
∴AE=BD,∠CDB=∠E=45°.
又∠EDC=45°,
∴∠ADB=90°.
在Rt△ADB中,AD2+DB2=AB2,易得AD2+AE2=AC2+CB2,
即AE2+AD2=2AC2.
备选习题
https://www.21cnjy.com/help/help_extract.php
