17.2.1 勾股定理的逆定理 课件(共29页)
文档属性
| 名称 | 17.2.1 勾股定理的逆定理 课件(共29页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 21:21:20 | ||
图片预览








文档简介
(共29张PPT)
17.2 勾股定理的逆定理
人教版八下数学
第1课时 勾股定理的逆定理
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
B
C
A
问题1 勾股定理的内容是什么
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
b
c
a
问题2 求以线段a、b为直角边的直角三角形的斜边c的长:
① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.
c=5
c=6.5
c=8.5
勾股定理的逆定理
1
问题引入
你们知道古埃及人用什么方法得到直角的吗
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
思考 以前我们已经学过了通过角的关系来确定直角三角形,可不可以通过边来确定直角三角形呢?
自主学习
讲授新课
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
是
自主学习
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题2 这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
问题3 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
自主学习
问题3 据此你有什么猜想呢
由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
自主学习
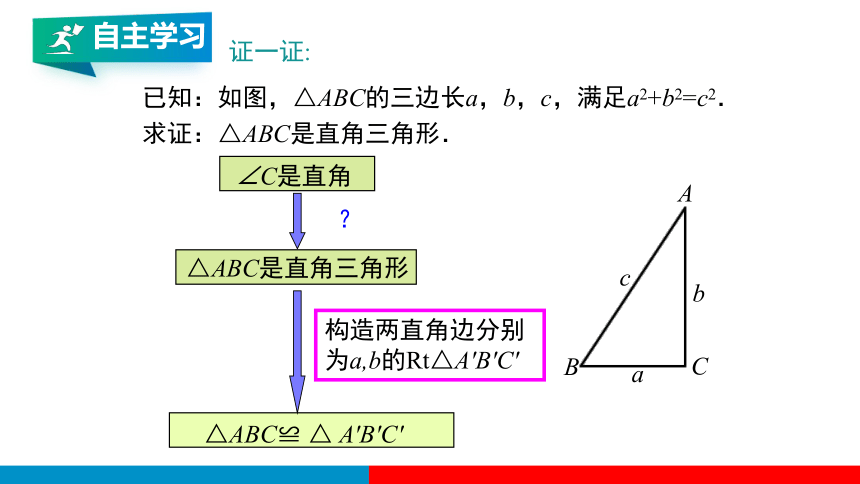
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
证一证:
自主学习
证明:作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,
∴△ABC≌ △A′B′C′(SSS),
∴∠C= ∠C′=90° , 即△ABC是直角三角形.
则
A
C
a
B
b
c
自主学习
勾股定理的逆定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
互逆定理
自主学习
特别提醒
勾股定理的逆定理是判定直角三角形的一个依据,在判定时不能说“在直角三角形中”“直角边”“斜边”,因为还没有确定是直角三角形.
a2+b2=c2只是一种表现形式,满足a2=b2+c2或b2=a2+c2的也是直角三角形,只是这时a或b为斜边长.
自主学习
例1
判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c =15.
典例分析
分析:根据勾股定理及其逆定理,判断一个三角形是不是直
角三角形,只要看两条较小边长的平方和是否等于最
大边长的平方.
解:(1)因为 152+82=225+64=289,172 = 289,所以152 +82 =172 ,
根据勾股定理的逆定理,这个三角形是直角三角形.
(2)因为132+142=169+196=365,152=225,所以132+142≠
152,根据勾股定理,这个三角形不是直角三角形.
典例分析
【变式题1】若△ABC的三边a,b,c满足 a:b: c=3:4:5,试判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
典例分析
拓展提高: 若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴△ABC是直角三角形.
典例分析
逆命题、逆定理
2
如果两个命题的题设、结论正好相反,那么这
两个命题称为互逆命题,如果把其中一个叫做
原命题,那么另一个叫做它的逆命题.
自主学习
2.如果一个定理的逆命题经过证明是正确的,那
么它也是一个定理,称其为原定理的逆定理,
这两个定理称为互逆定理.
特别警示
判断一个命题是真命题需要证明,而判断一个命题是假命题,只需举一个反例即可.
自主学习
例 2
判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
典例分析
解:(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
典例分析
总 结
写出逆命题的关键是分清楚原命题的题设和结论,
然后将它的题设和结论交换位置就得到这个命题的逆
命题.判断一个命题是真命题需要进行逻辑推理,判
断一个命题是假命题只需要举出一个反例就可以了.
典例分析
1.
说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)在角的内部,到角的两边距离相等的点在角
的平分线上.
课堂练习
(1)逆命题:内错角相等,两条直线平行.逆命题成立.
(2)逆命题:如果两个实数的绝对值相等,那么这
两个实数相等.逆命题不成立.
(3)逆命题:三个角对应相等的两个三角形全等.
逆命题不成立.
(4)逆命题:角的平分线上的点到角两边的距离相等.
逆命题成立.
解:
课堂练习
总 结
判断一个三角形是不是直角三角形有两种方法:
(1)利用定义,即如果已知条件与角度有关,可借助三角
形的内角和定理判断;
(2)利用直角三角形的判定条件,即若已知条件与边有关,
一般通过计算得出三边的数量关系(即a2+b2=c2)来判
断,看是否符合较短两边的平方和等于最长边的平方.
自主学习
勾股定理的逆定理
逆定理
三角形两直角边分
别为a,b,斜边为
c,那么a2+b2=c2
定理
直角三角形!
1.判断由线段a,b,c组成的三角形是不是直角三角形:
(1) a=7,b=24,c=25; (2) a= ,b=4,c=5;
(3) a= ,b=1,c= ; (4) a=40,b=50,c=60.
解: (1) a2+b2=625=c2,是直角三角形.
(2) b2+c2=41=a2,是直角三角形.
(3) b2+c2= =a2,是直角三角形.
(4) 不是直角三角形.
备选习题
2.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1) 同旁内角互补,两直线平行;
(2) 如果两个角是直角,那么它们相等;
解: (1) 两直线平行,同旁内角互补.成立.
(2) 如果两个角相等,那么这两个角是直角.不成立.
备选习题
(3) 全等三角形的对应边相等;
(4) 如果两个实数相等,那么它们的平方相等.
(3) 三条边对应相等的三角形全等.成立.
(4) 如果两个实数的平方相等,那么这两个实数相等.
不成立.
备选习题
https://www.21cnjy.com/help/help_extract.php
17.2 勾股定理的逆定理
人教版八下数学
第1课时 勾股定理的逆定理
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
B
C
A
问题1 勾股定理的内容是什么
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
b
c
a
问题2 求以线段a、b为直角边的直角三角形的斜边c的长:
① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.
c=5
c=6.5
c=8.5
勾股定理的逆定理
1
问题引入
你们知道古埃及人用什么方法得到直角的吗
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
思考 以前我们已经学过了通过角的关系来确定直角三角形,可不可以通过边来确定直角三角形呢?
自主学习
讲授新课
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
是
自主学习
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题2 这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
问题3 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
自主学习
问题3 据此你有什么猜想呢
由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
自主学习
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
证一证:
自主学习
证明:作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,
∴△ABC≌ △A′B′C′(SSS),
∴∠C= ∠C′=90° , 即△ABC是直角三角形.
则
A
C
a
B
b
c
自主学习
勾股定理的逆定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
互逆定理
自主学习
特别提醒
勾股定理的逆定理是判定直角三角形的一个依据,在判定时不能说“在直角三角形中”“直角边”“斜边”,因为还没有确定是直角三角形.
a2+b2=c2只是一种表现形式,满足a2=b2+c2或b2=a2+c2的也是直角三角形,只是这时a或b为斜边长.
自主学习
例1
判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c =15.
典例分析
分析:根据勾股定理及其逆定理,判断一个三角形是不是直
角三角形,只要看两条较小边长的平方和是否等于最
大边长的平方.
解:(1)因为 152+82=225+64=289,172 = 289,所以152 +82 =172 ,
根据勾股定理的逆定理,这个三角形是直角三角形.
(2)因为132+142=169+196=365,152=225,所以132+142≠
152,根据勾股定理,这个三角形不是直角三角形.
典例分析
【变式题1】若△ABC的三边a,b,c满足 a:b: c=3:4:5,试判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
典例分析
拓展提高: 若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴△ABC是直角三角形.
典例分析
逆命题、逆定理
2
如果两个命题的题设、结论正好相反,那么这
两个命题称为互逆命题,如果把其中一个叫做
原命题,那么另一个叫做它的逆命题.
自主学习
2.如果一个定理的逆命题经过证明是正确的,那
么它也是一个定理,称其为原定理的逆定理,
这两个定理称为互逆定理.
特别警示
判断一个命题是真命题需要证明,而判断一个命题是假命题,只需举一个反例即可.
自主学习
例 2
判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
典例分析
解:(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
典例分析
总 结
写出逆命题的关键是分清楚原命题的题设和结论,
然后将它的题设和结论交换位置就得到这个命题的逆
命题.判断一个命题是真命题需要进行逻辑推理,判
断一个命题是假命题只需要举出一个反例就可以了.
典例分析
1.
说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)在角的内部,到角的两边距离相等的点在角
的平分线上.
课堂练习
(1)逆命题:内错角相等,两条直线平行.逆命题成立.
(2)逆命题:如果两个实数的绝对值相等,那么这
两个实数相等.逆命题不成立.
(3)逆命题:三个角对应相等的两个三角形全等.
逆命题不成立.
(4)逆命题:角的平分线上的点到角两边的距离相等.
逆命题成立.
解:
课堂练习
总 结
判断一个三角形是不是直角三角形有两种方法:
(1)利用定义,即如果已知条件与角度有关,可借助三角
形的内角和定理判断;
(2)利用直角三角形的判定条件,即若已知条件与边有关,
一般通过计算得出三边的数量关系(即a2+b2=c2)来判
断,看是否符合较短两边的平方和等于最长边的平方.
自主学习
勾股定理的逆定理
逆定理
三角形两直角边分
别为a,b,斜边为
c,那么a2+b2=c2
定理
直角三角形!
1.判断由线段a,b,c组成的三角形是不是直角三角形:
(1) a=7,b=24,c=25; (2) a= ,b=4,c=5;
(3) a= ,b=1,c= ; (4) a=40,b=50,c=60.
解: (1) a2+b2=625=c2,是直角三角形.
(2) b2+c2=41=a2,是直角三角形.
(3) b2+c2= =a2,是直角三角形.
(4) 不是直角三角形.
备选习题
2.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1) 同旁内角互补,两直线平行;
(2) 如果两个角是直角,那么它们相等;
解: (1) 两直线平行,同旁内角互补.成立.
(2) 如果两个角相等,那么这两个角是直角.不成立.
备选习题
(3) 全等三角形的对应边相等;
(4) 如果两个实数相等,那么它们的平方相等.
(3) 三条边对应相等的三角形全等.成立.
(4) 如果两个实数的平方相等,那么这两个实数相等.
不成立.
备选习题
https://www.21cnjy.com/help/help_extract.php
