2021-2022学年人教版八年级数学下册第16章二次根式 自主提升训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册第16章二次根式 自主提升训练 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 16:00:18 | ||
图片预览


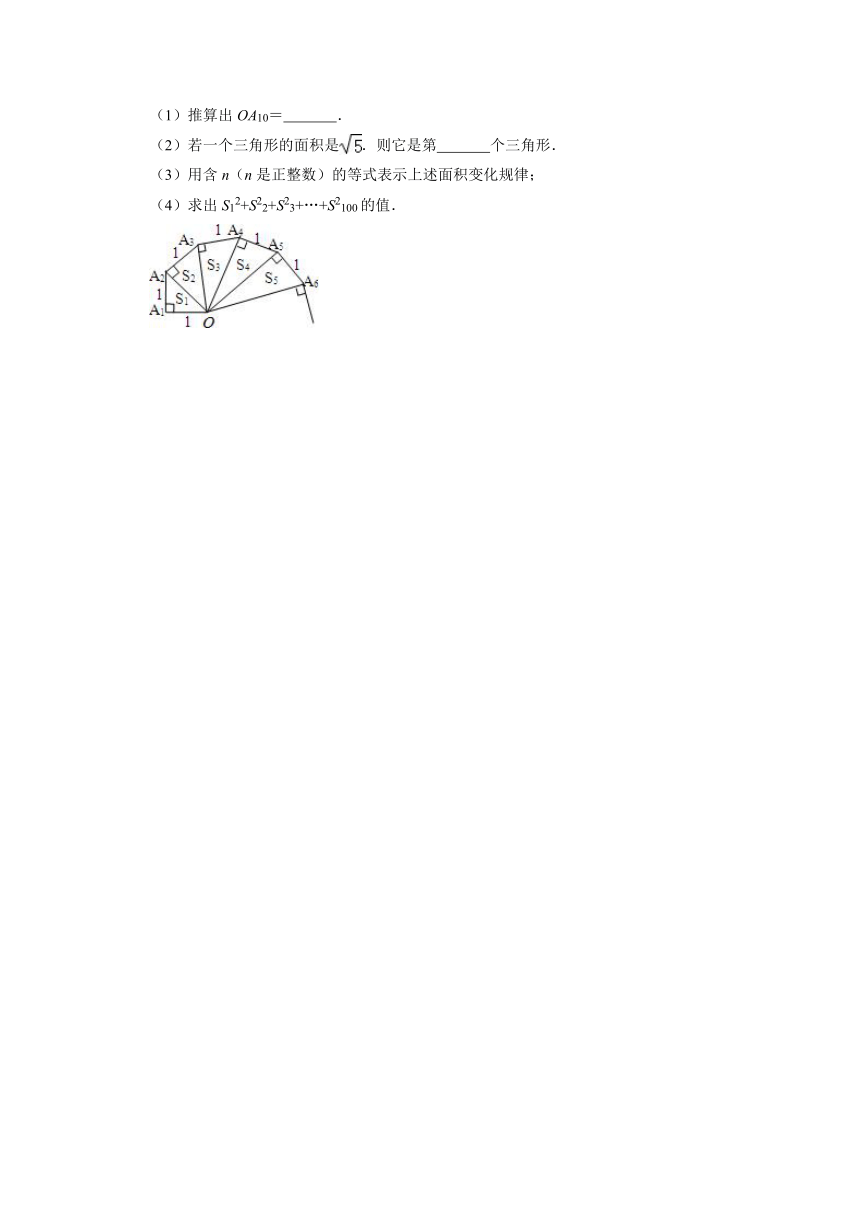

文档简介
2021-2022学年人教版八年级数学下册《第16章二次根式》自主提升训练(附答案)
1.已知,则=( )
A. B.﹣ C. D.
2.若代数式有意义,则实数x的取值范围是( )
A.x>1 B.x≠2 C.x≥1且x≠2 D.x≥﹣1且x≠2
3.当a=﹣2时,二次根式的值是 .
4.若代数式有意义,则x的取值范围为 .
5.若是一个正整数,则正整数m的最小值是 .
6.观察分析下列数据,寻找规律:0,,,3,2…那么第10个数据应是 .
7.若二次根式有意义,则x的取值范围是 .
8.计算= .
9.若和都是最简二次根式,则m= ,n= .
10.当x= 时,既是最简二次根式,被开方数又相同.
11.使等式成立的条件是 .
12.已知a=3+2,b=3﹣2,则a2b﹣ab2= .
13.若最简二次根式与被开方数相同,则a的值为 .
14.计算﹣的结果是 .
15.计算:(﹣2)2020×(+2)2021的结果是 .
16.若,则x2+2x+1= .
17.观察分析下列数据:0,﹣,,﹣3,2,﹣,3,…,根据数据排列的规律得到第13个数据应是 .
18.已知x、y都是实数,且,求yx的平方根.
19.已知:x,y为实数,且,化简:.
20.已知a,b是有理数,若+2=b+4,求a和b的值.
21.已知数a满足=a,求a﹣20242的值.
22.观察下列各式:①=2,②=3;③=4,…
(1)请观察规律,并写出第④个等式: ;
(2)请用含n(n≥1)的式子写出你猜想的规律: ;
(3)请证明(2)中的结论.
23.已知x为奇数,且,求的值.
24.计算:.
25.阅读下列解题过程:
;请回答下列问题:
(1)观察上面的解题过程,化简:①②
(2)利用上面提供的解法,请计算:
.
26.如果最简二次根式与是同类二次根式.
(1)求出a的值;
(2)若a≤x≤2a,化简:+.
27.已知:a=﹣1,b=+1.
求:(1)a﹣b的值;
(2)ab的值;
(3)的值.
28.计算
(1)﹣4+÷
(2)(1﹣)2﹣+()0.
29.已知:a=,b=.
求值:(1)ab;
(2)a2﹣3ab+b2;
30.细心观察图形,认真分析各式,然后解答问题:
OA1=1;
OA2==; S1=×1×1=;
OA3==; S2=××1=;
OA4==; S3=××1=;
(1)推算出OA10= .
(2)若一个三角形的面积是.则它是第 个三角形.
(3)用含n(n是正整数)的等式表示上述面积变化规律;
(4)求出S12+S22+S23+…+S2100的值.
参考答案
1.解:∵()2=(a+)2﹣4
=7﹣4=3,
∴=±.
故选:C.
2.解:由题意得,x+1≥0且(x﹣2)2≠0,
解得x≥﹣1且x≠2.
故选:D.
3.解:当a=﹣2时,二次根式==2.
4.解:∵代数式有意义,
∴x﹣3>0,
∴x>3,
∴x的取值范围是x>3,
故答案为:x>3.
5.解:∵是一个正整数,且=2,
∴5m是一个完全平方数,
∴m=5n2,n为正整数,
∴当n=1时,m取最小值5,
故答案为5.
6.解:0=,,,3=,2=,可以得到第10个数的被开方数一定能是3的9倍,则第10个数是:==3.
故答案是:3.
7.解:根据题意得,2x﹣3≥0,
解得x≥.
故答案为:x≥.
8.解:==2,
故答案为:2.
9.解:∵若和都是最简二次根式,
∴,
解得:m=1,n=2,
故答案为:1;2.
10.解:若既是最简二次根式,
则x2+3x=x+15,
解得x=﹣5或3,
当x=3时,被开方数x+15=18,两式不是最简二次根式,
故x=﹣5.
11.解:根据题意得,,
解得x≥1.
故答案为:x≥1.
12.解:∵a=3+2,b=3﹣2,
∴ab=9﹣8=1,a﹣b=4,
∴原式=ab(a﹣b)=4,
故答案为:4
13.解:∵最简二次根式与是同类二次根式,
∴2a﹣3=5,
解得:a=4.
故答案为:4.
14.解:原式=﹣2
=﹣.
故答案为:﹣.
15.解:原式=[(﹣2)(+2)]2020(+2)
=+2,
故答案为:+2.
16.解:原式=(x+1)2,
当x=﹣1时,原式=()2=2.
17.解:由题意知道:题目中的数据可以整理为:(﹣1)1+1,(﹣1)2+1,…(﹣1)n+1),
∴第13个答案为:(﹣1)13+1=6.
故答案为:6.
18.解:∵负数不能开平方,
∴,
∴x=3,y=4,
∴yx=43=64,
∴±=±8.
19.解:依题意,得
∴x﹣1=0,解得:x=1
∴y<3
∴y﹣3<0,y﹣4<0
∴
=3﹣y﹣
=3﹣y﹣(4﹣y)
=﹣1.
20.解:根据题意得:,
解得:a=5,
则b+4=0,解得:b=﹣4.
21.解:根据二次根式的性质可得,a﹣2025≥0,即a≥2025,
由原式可得,a﹣2024+=a
∴=2024
∴a﹣2025=20242
∴a﹣20242=2025.
22.解:(1)=5;
(2)=(n+1);
(3)
=
=
=
=(n+1).
故答案为:(1)=5;
(2))=(n+1).
23.解:∵,
∴,解得6≤x<9;
又∵x为奇数,
∴x=7,
∴
=+
=+
=8+2.
24.解:原式=(3)2﹣(4)2=54﹣32=22.
25.解:(1)①==+3;
②==;
(2)
=(﹣+﹣+﹣+…+﹣)(+)
=(﹣)(+)
=n.
26.解:(1)∵最简二次根式与是同类二次根式,
∴4a﹣5=13﹣2a,
解得:a=3;
(2)把a=3代入得:3≤x≤6,
则原式=+=|x﹣2|+|x﹣6|=x﹣2+6﹣x=4.
27.解:(1)当a=﹣1,b=+1时,
a﹣b=﹣1﹣(+1)
=﹣1﹣﹣1
=﹣2;
(2)ab=(﹣1)(+1)
=()2﹣12
=2﹣1
=1;
(3)原式=
=
=
=4+2
=6.
28.解:(1)原式=3﹣2+
=3﹣2+2
=3;
(2)原式=1﹣2+2﹣3(﹣1)+1
=3﹣2﹣3+3+1
=7﹣5.
29.解:(1)ab=(+)(﹣)
=5﹣3
=2.
(2)a﹣b=+﹣+
=2,
∴a2﹣3ab+b2=(a﹣b)2﹣ab
=12﹣2
=10.
30.解:(1))∵OAn2=n,
∴OA10=.
故答案为:;
(2)若一个三角形的面积是,
∵Sn==,
∴=2=,
∴它是第20个三角形.
故答案为:20;
(3)结合已知数据,可得:OAn2=n;Sn=;
(4)S12+S22+S23+…+S2100
=++++…+
=
=
1.已知,则=( )
A. B.﹣ C. D.
2.若代数式有意义,则实数x的取值范围是( )
A.x>1 B.x≠2 C.x≥1且x≠2 D.x≥﹣1且x≠2
3.当a=﹣2时,二次根式的值是 .
4.若代数式有意义,则x的取值范围为 .
5.若是一个正整数,则正整数m的最小值是 .
6.观察分析下列数据,寻找规律:0,,,3,2…那么第10个数据应是 .
7.若二次根式有意义,则x的取值范围是 .
8.计算= .
9.若和都是最简二次根式,则m= ,n= .
10.当x= 时,既是最简二次根式,被开方数又相同.
11.使等式成立的条件是 .
12.已知a=3+2,b=3﹣2,则a2b﹣ab2= .
13.若最简二次根式与被开方数相同,则a的值为 .
14.计算﹣的结果是 .
15.计算:(﹣2)2020×(+2)2021的结果是 .
16.若,则x2+2x+1= .
17.观察分析下列数据:0,﹣,,﹣3,2,﹣,3,…,根据数据排列的规律得到第13个数据应是 .
18.已知x、y都是实数,且,求yx的平方根.
19.已知:x,y为实数,且,化简:.
20.已知a,b是有理数,若+2=b+4,求a和b的值.
21.已知数a满足=a,求a﹣20242的值.
22.观察下列各式:①=2,②=3;③=4,…
(1)请观察规律,并写出第④个等式: ;
(2)请用含n(n≥1)的式子写出你猜想的规律: ;
(3)请证明(2)中的结论.
23.已知x为奇数,且,求的值.
24.计算:.
25.阅读下列解题过程:
;请回答下列问题:
(1)观察上面的解题过程,化简:①②
(2)利用上面提供的解法,请计算:
.
26.如果最简二次根式与是同类二次根式.
(1)求出a的值;
(2)若a≤x≤2a,化简:+.
27.已知:a=﹣1,b=+1.
求:(1)a﹣b的值;
(2)ab的值;
(3)的值.
28.计算
(1)﹣4+÷
(2)(1﹣)2﹣+()0.
29.已知:a=,b=.
求值:(1)ab;
(2)a2﹣3ab+b2;
30.细心观察图形,认真分析各式,然后解答问题:
OA1=1;
OA2==; S1=×1×1=;
OA3==; S2=××1=;
OA4==; S3=××1=;
(1)推算出OA10= .
(2)若一个三角形的面积是.则它是第 个三角形.
(3)用含n(n是正整数)的等式表示上述面积变化规律;
(4)求出S12+S22+S23+…+S2100的值.
参考答案
1.解:∵()2=(a+)2﹣4
=7﹣4=3,
∴=±.
故选:C.
2.解:由题意得,x+1≥0且(x﹣2)2≠0,
解得x≥﹣1且x≠2.
故选:D.
3.解:当a=﹣2时,二次根式==2.
4.解:∵代数式有意义,
∴x﹣3>0,
∴x>3,
∴x的取值范围是x>3,
故答案为:x>3.
5.解:∵是一个正整数,且=2,
∴5m是一个完全平方数,
∴m=5n2,n为正整数,
∴当n=1时,m取最小值5,
故答案为5.
6.解:0=,,,3=,2=,可以得到第10个数的被开方数一定能是3的9倍,则第10个数是:==3.
故答案是:3.
7.解:根据题意得,2x﹣3≥0,
解得x≥.
故答案为:x≥.
8.解:==2,
故答案为:2.
9.解:∵若和都是最简二次根式,
∴,
解得:m=1,n=2,
故答案为:1;2.
10.解:若既是最简二次根式,
则x2+3x=x+15,
解得x=﹣5或3,
当x=3时,被开方数x+15=18,两式不是最简二次根式,
故x=﹣5.
11.解:根据题意得,,
解得x≥1.
故答案为:x≥1.
12.解:∵a=3+2,b=3﹣2,
∴ab=9﹣8=1,a﹣b=4,
∴原式=ab(a﹣b)=4,
故答案为:4
13.解:∵最简二次根式与是同类二次根式,
∴2a﹣3=5,
解得:a=4.
故答案为:4.
14.解:原式=﹣2
=﹣.
故答案为:﹣.
15.解:原式=[(﹣2)(+2)]2020(+2)
=+2,
故答案为:+2.
16.解:原式=(x+1)2,
当x=﹣1时,原式=()2=2.
17.解:由题意知道:题目中的数据可以整理为:(﹣1)1+1,(﹣1)2+1,…(﹣1)n+1),
∴第13个答案为:(﹣1)13+1=6.
故答案为:6.
18.解:∵负数不能开平方,
∴,
∴x=3,y=4,
∴yx=43=64,
∴±=±8.
19.解:依题意,得
∴x﹣1=0,解得:x=1
∴y<3
∴y﹣3<0,y﹣4<0
∴
=3﹣y﹣
=3﹣y﹣(4﹣y)
=﹣1.
20.解:根据题意得:,
解得:a=5,
则b+4=0,解得:b=﹣4.
21.解:根据二次根式的性质可得,a﹣2025≥0,即a≥2025,
由原式可得,a﹣2024+=a
∴=2024
∴a﹣2025=20242
∴a﹣20242=2025.
22.解:(1)=5;
(2)=(n+1);
(3)
=
=
=
=(n+1).
故答案为:(1)=5;
(2))=(n+1).
23.解:∵,
∴,解得6≤x<9;
又∵x为奇数,
∴x=7,
∴
=+
=+
=8+2.
24.解:原式=(3)2﹣(4)2=54﹣32=22.
25.解:(1)①==+3;
②==;
(2)
=(﹣+﹣+﹣+…+﹣)(+)
=(﹣)(+)
=n.
26.解:(1)∵最简二次根式与是同类二次根式,
∴4a﹣5=13﹣2a,
解得:a=3;
(2)把a=3代入得:3≤x≤6,
则原式=+=|x﹣2|+|x﹣6|=x﹣2+6﹣x=4.
27.解:(1)当a=﹣1,b=+1时,
a﹣b=﹣1﹣(+1)
=﹣1﹣﹣1
=﹣2;
(2)ab=(﹣1)(+1)
=()2﹣12
=2﹣1
=1;
(3)原式=
=
=
=4+2
=6.
28.解:(1)原式=3﹣2+
=3﹣2+2
=3;
(2)原式=1﹣2+2﹣3(﹣1)+1
=3﹣2﹣3+3+1
=7﹣5.
29.解:(1)ab=(+)(﹣)
=5﹣3
=2.
(2)a﹣b=+﹣+
=2,
∴a2﹣3ab+b2=(a﹣b)2﹣ab
=12﹣2
=10.
30.解:(1))∵OAn2=n,
∴OA10=.
故答案为:;
(2)若一个三角形的面积是,
∵Sn==,
∴=2=,
∴它是第20个三角形.
故答案为:20;
(3)结合已知数据,可得:OAn2=n;Sn=;
(4)S12+S22+S23+…+S2100
=++++…+
=
=
