2021-2022学年高一下学期数学北师大版(2019)必修二第二册4.1同角三角函数的基本关系课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修二第二册4.1同角三角函数的基本关系课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 21:05:17 | ||
图片预览










文档简介
(共34张PPT)
4.1 同角三角函数的基本关系
北师大(2019)必修2
聚焦知识目标
1.理解同角三角函数的基本关系: x
2.会用同角三角函数的基本关系进行三角函数式的求值、化简和证明
数学素养
1.通过基本关系推理,培养学生逻辑推理素养
2.通过基本关系的应用,培养数学运算素养
情境引入
情境引入
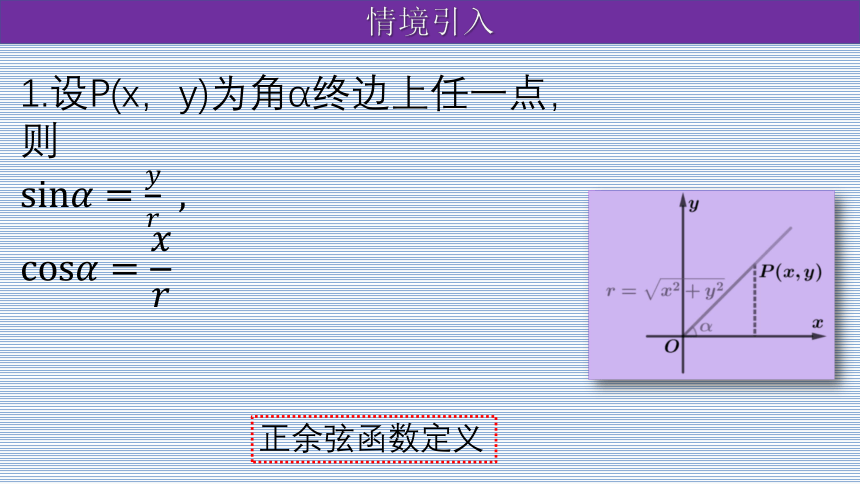
1.设P(x,y)为角α终边上任一点,则
正余弦函数定义
情境引入
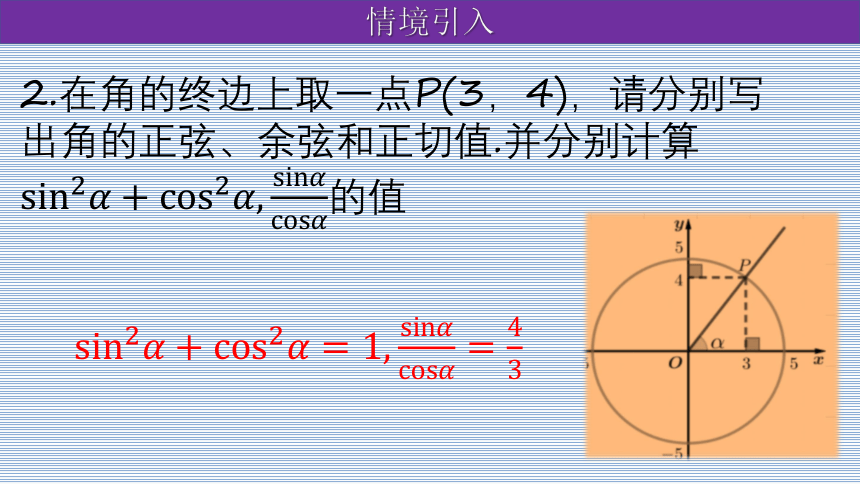
2.在角的终边上取一点P(3,4),请分别写出角的正弦、余弦和正切值.并分别计算 的值
情境引入
3. 计算下列各式的值:
1
1
通过上面的计算,你发现了什么特殊之处了吗?
情境引入
如图,任意角a的终边与单位圆的交点P的坐标是(cos a. sina),点P到坐标原点O的距离为1,所以P(cosα. sinα)
另外,由正切函数的定义,
这两个关系式是同角三角函数的基本关系式.
同角三角函数的基本关系
同角三角函数的基本关系
同角三角函数的基本关系理解
(1)“同角”有两层含义:一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下),关系式都成立,与角的表达形式无关.
例
(2)注意公式成立的条件.
(3)注意公式的变形,特别是公式的逆用.
(4)在应用平方关系式求sina或cosa时,其正负号是由角α所在的象限决定.
辨析
同角三角函数的基本关系变形
同角三角函数的基本关系应用
由一个三角函数值求其他三角函数值
由角α的某一个三角函数值,利用平方关系和商数关系这两个关系式,可以求出其他三角函数值.
由一个三角函数值求其他三角函数值
1.已知正弦求余弦和正切值
例1已知 且角a的终边在第二象限,求cosa和tanα的值.
解:由【平方关系】有
又角α的终边在第二象限. cosa<0,所以,
再由【商数关系】有
由一个三角函数值求其他三角函数值
2.已知余弦求正弦和正切值
例2已知 求sina和tana的值.
解:由【平方关系】有
因为 所以角a的终边在第二或第三象限
当a的终边在第二象限时,
由一个三角函数值求其他三角函数值
2.已知余弦求正弦和正切值
例2已知 求sina和tana的值.
解:由【平方关系】有
因为 所以角a的终边在第二或第三象限
当a的终边在第三象限时,sin a<0,
注意角的象限
由一个三角函数值求其他三角函数值
3.已知正切求正弦和余弦值
例3.已知 且φ是第二象限角,求角φ的正弦值和余弦值.
由 得
代入 得
又因为φ是第二象限角,
所以
先商后方,代入消元法
由一个三角函数值求其他三角函数值
3.已知正切求正弦和余弦值
例4.已知tanα=m,求sina和cosα的值.
综合应用
例5.已知sin 求tan a的值.
解:对 两边平方,再利用 1.消去cosα,得25a+5sina-12=0.解方程,得 或sina=-
因为 所以sina=- ,代入已知条件,得
综合应用
例6.已知 求
解因为 所以cos a≠0.
所以
本题的解法比较巧妙,并不需要求得sina和cosa的值.但如果题目换成求 呢?
综合应用
综合应用
证明恒等式,既可以利用恒等式的“左式减右式为零”进行证明,也可以证明恒等式的左右式、右式分别等于同一个式子.
综合应用
例7求证:
证明,由cos a0,知sin a≠1.所以1-sin a0.于是
==0.
所以原式成立.
综合应用
例8
学以致用
1.
2.
3.
4.1 同角三角函数的基本关系
北师大(2019)必修2
聚焦知识目标
1.理解同角三角函数的基本关系: x
2.会用同角三角函数的基本关系进行三角函数式的求值、化简和证明
数学素养
1.通过基本关系推理,培养学生逻辑推理素养
2.通过基本关系的应用,培养数学运算素养
情境引入
情境引入
1.设P(x,y)为角α终边上任一点,则
正余弦函数定义
情境引入
2.在角的终边上取一点P(3,4),请分别写出角的正弦、余弦和正切值.并分别计算 的值
情境引入
3. 计算下列各式的值:
1
1
通过上面的计算,你发现了什么特殊之处了吗?
情境引入
如图,任意角a的终边与单位圆的交点P的坐标是(cos a. sina),点P到坐标原点O的距离为1,所以P(cosα. sinα)
另外,由正切函数的定义,
这两个关系式是同角三角函数的基本关系式.
同角三角函数的基本关系
同角三角函数的基本关系
同角三角函数的基本关系理解
(1)“同角”有两层含义:一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下),关系式都成立,与角的表达形式无关.
例
(2)注意公式成立的条件.
(3)注意公式的变形,特别是公式的逆用.
(4)在应用平方关系式求sina或cosa时,其正负号是由角α所在的象限决定.
辨析
同角三角函数的基本关系变形
同角三角函数的基本关系应用
由一个三角函数值求其他三角函数值
由角α的某一个三角函数值,利用平方关系和商数关系这两个关系式,可以求出其他三角函数值.
由一个三角函数值求其他三角函数值
1.已知正弦求余弦和正切值
例1已知 且角a的终边在第二象限,求cosa和tanα的值.
解:由【平方关系】有
又角α的终边在第二象限. cosa<0,所以,
再由【商数关系】有
由一个三角函数值求其他三角函数值
2.已知余弦求正弦和正切值
例2已知 求sina和tana的值.
解:由【平方关系】有
因为 所以角a的终边在第二或第三象限
当a的终边在第二象限时,
由一个三角函数值求其他三角函数值
2.已知余弦求正弦和正切值
例2已知 求sina和tana的值.
解:由【平方关系】有
因为 所以角a的终边在第二或第三象限
当a的终边在第三象限时,sin a<0,
注意角的象限
由一个三角函数值求其他三角函数值
3.已知正切求正弦和余弦值
例3.已知 且φ是第二象限角,求角φ的正弦值和余弦值.
由 得
代入 得
又因为φ是第二象限角,
所以
先商后方,代入消元法
由一个三角函数值求其他三角函数值
3.已知正切求正弦和余弦值
例4.已知tanα=m,求sina和cosα的值.
综合应用
例5.已知sin 求tan a的值.
解:对 两边平方,再利用 1.消去cosα,得25a+5sina-12=0.解方程,得 或sina=-
因为 所以sina=- ,代入已知条件,得
综合应用
例6.已知 求
解因为 所以cos a≠0.
所以
本题的解法比较巧妙,并不需要求得sina和cosa的值.但如果题目换成求 呢?
综合应用
综合应用
证明恒等式,既可以利用恒等式的“左式减右式为零”进行证明,也可以证明恒等式的左右式、右式分别等于同一个式子.
综合应用
例7求证:
证明,由cos a0,知sin a≠1.所以1-sin a0.于是
==0.
所以原式成立.
综合应用
例8
学以致用
1.
2.
3.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
