2021-2022学年高二上学期数学 人教B版(2019)必修第四册空中直线、平面的平行 讲义 (学生版)
文档属性
| 名称 | 2021-2022学年高二上学期数学 人教B版(2019)必修第四册空中直线、平面的平行 讲义 (学生版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 00:00:00 | ||
图片预览


文档简介
空间中直线、平面的平行
【课前诊断】
成绩(满分10): 完成情况: 优/中/差
1. 已知是两条异面直线,那么与的位置关系__________.
2. 判断正误
(1)两个不重合的平面只能把空间分成四个部分
(2)两个平面有一个公共点,就说相交于点,记作
(3)两两相交的三条直线最多可以确定三个平面
(4)如果两个平面有三个公共点,则这两个平面重合
3. 如图所示,在正方体中,分别是的中点.
求证:(1)四点共面;
(2)三线共点.
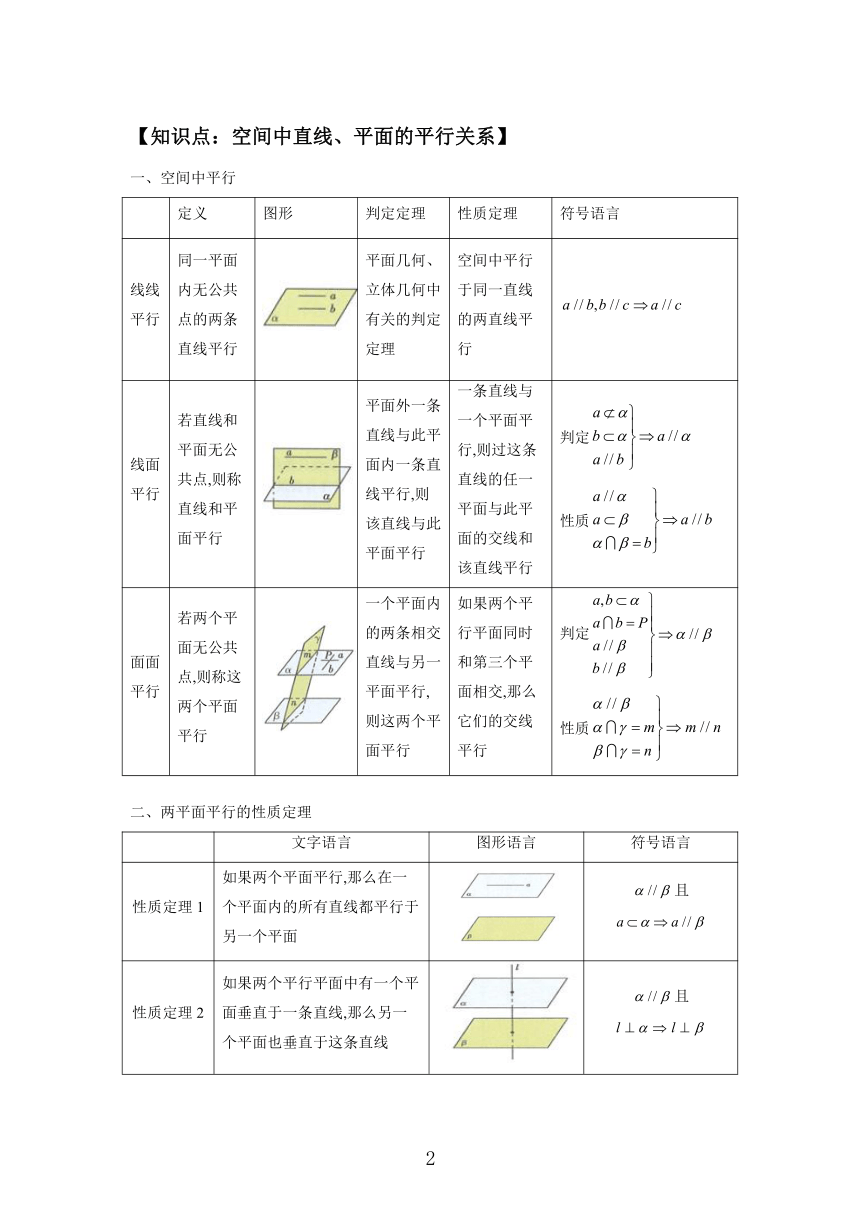
【知识点:空间中直线、平面的平行关系】
一、空间中平行
定义 图形 判定定理 性质定理 符号语言
线线平行 同一平面内无公共点的两条直线平行 平面几何、立体几何中有关的判定定理 空间中平行于同一直线的两直线平行
线面平行 若直线和平面无公共点,则称直线和平面平行 平面外一条直线与此平面内一条直线平行,则该直线与此平面平行 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线和该直线平行 判定 性质
面面平行 若两个平面无公共点,则称这两个平面平行 一个平面内的两条相交直线与另一平面平行,则这两个平面平行 如果两个平行平面同时和第三个平面相交,那么它们的交线平行 判定性质
二、两平面平行的性质定理
文字语言 图形语言 符号语言
性质定理1 如果两个平面平行,那么在一个平面内的所有直线都平行于另一个平面 且
性质定理2 如果两个平行平面中有一个平面垂直于一条直线,那么另一个平面也垂直于这条直线 且
三、线线平行、线面平行、面面平行间的关系
由于三者之间相互沟通、相互联系,因此立体几何问题的解决往往可以一题多解(证).
【典型例题】
考点一:空间中直线与平面的平行
题型一:直接法
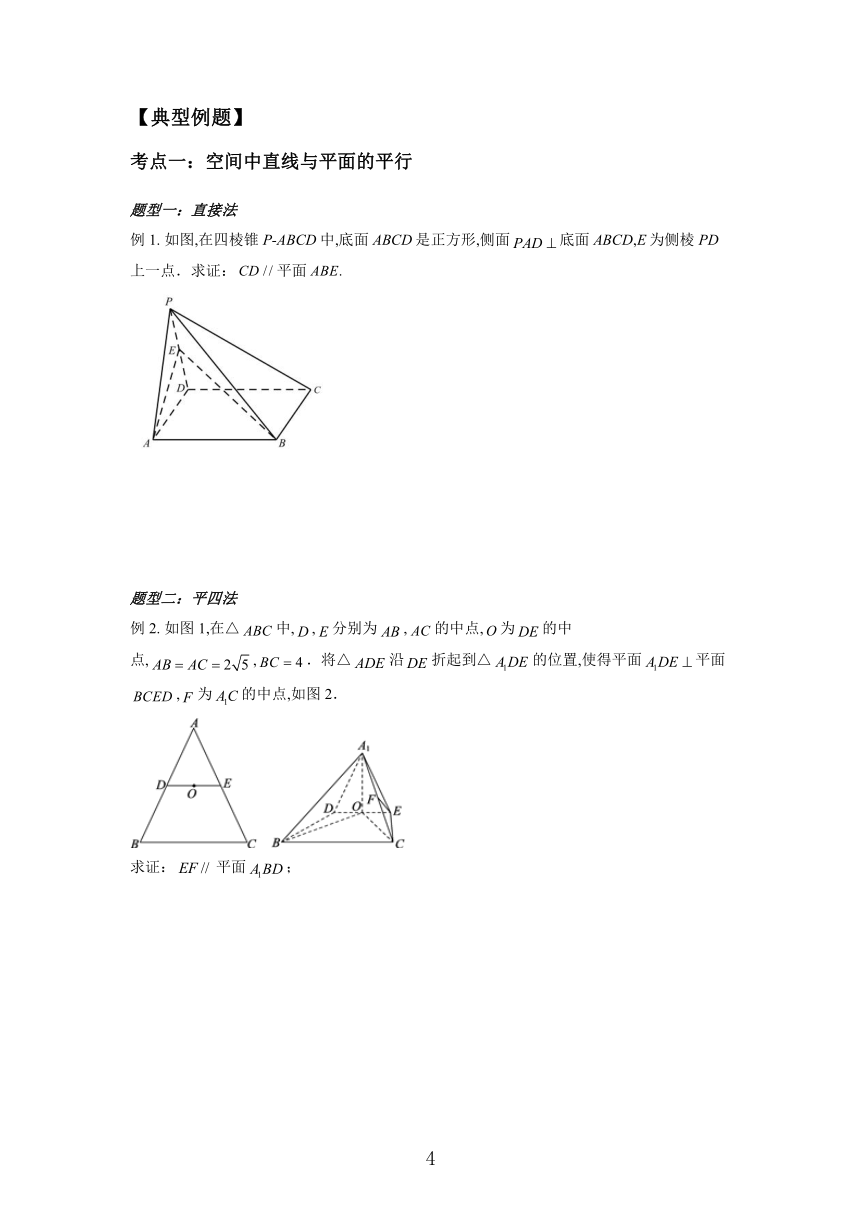
例1. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面底面ABCD,E为侧棱PD上一点.求证:平面
求证:平面ABE;
【答案】
题型二:平四法
例2. 如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△的位置,使得平面平面,为的中点,如图2.
求证:平面;
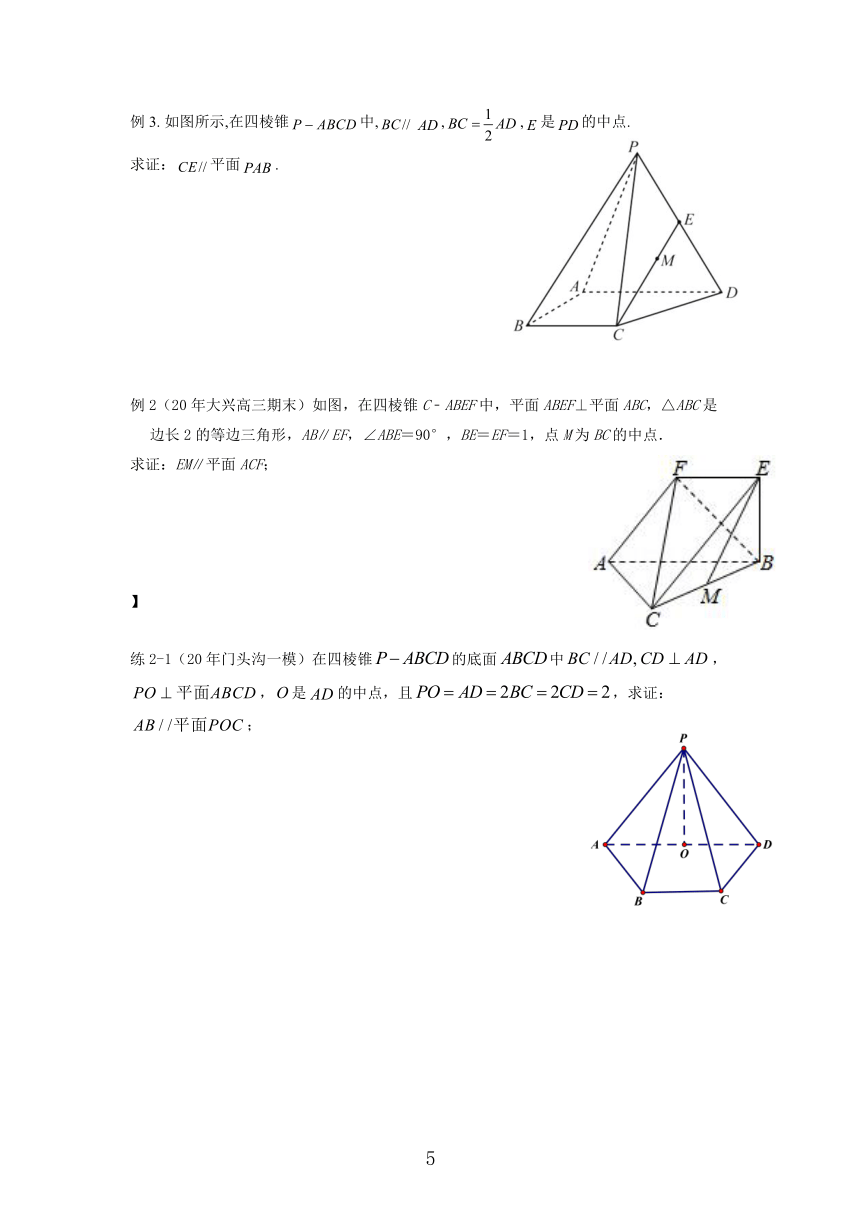
例3. 如图所示,在四棱锥中,,,是的中点.
求证:平面.
例2(20年大兴高三期末)如图,在四棱锥C﹣ABEF中,平面ABEF⊥平面ABC,△ABC是边长2的等边三角形,AB∥EF,∠ABE=90°,BE=EF=1,点M为BC的中点.
求证:EM∥平面ACF;
】
练2-1(20年门头沟一模)在四棱锥的底面中,,是的中点,且,求证:;
题型三:中位线法
例1(20年海淀高三期末)如图,在三棱锥中,平面平面,和均是等腰直角三角形,,,,分别为, 的中点.
求证:平面;
练1(20年适应性测试)如图,在四棱锥中,,,,底面为正方形,分别为的中点.
(Ⅰ)求证:平面;
练2. 如图,四棱锥的底面是正方形,侧棱底面,E是的中点.
(1)求证:平面;
(2)求证:平面;
练1-1 (20年西城高三期末)如图,在三棱柱中,平面,为正三角形,侧面是边长为2的正方形,为的中点.
(I)求证:平面;
练3. 如图,在四棱锥中,底面是菱形,,平面,,,.
求证:直线平面PNC;
题型四:构造面面平行法
例3(2020北京十一学校高一下期末)如图,四棱锥中,,,分别为线段的中点,与交于点,是线段上的一点,求证:平面
练习3-1(2020北京101中学高一下期末)如图,三棱柱中,分别为中点,求证:平面
练习3-2(2016-2017房山高三理二模17)如图,正方形与梯形所在的平面互相垂直,已知,,
.
(Ⅰ)求证:平面;
考点二:空间中平面与平面的平行
例1. 如图,已知正方形所在平面和平行四边形所在平面互相垂直,平面平面,,是线段上的一点且平面.
求证:平面平面;
练1.(10-11海淀二模)
已知直三棱柱的所有棱长都相等,且分别为的中点.求证:平面平面;
练1. 如图,在多面体中,底面是边长为的正方形,四边形是矩形,平面平面,,和分别是和的中点.
求证:平面平面
例1.(2013-2014北大附检测)如图,为所在平面外一点,分别为的重心.求证:平面平面
考点三:空间中直线与直线的平行
例1. 如图所示,在四棱锥中,平面, ,是的中点.
求证:
例2. 在四棱锥中,底面为直角梯形,,,,为线段的中点. 底面,点是棱的中点,平面与棱相交于点.
求证:;
练1. 如图,正方形 的边长为2,分别为的中点,在五棱锥中,为棱的中点,平面与棱分别交于点.
求证:
练1. 如图,在四棱锥中,已知底面为平行四边形,点为棱的中点.
(1)求证:平面;
(2)设平面平面,点在上,求证:为的中点.
练2. 四棱锥,,平面,设平面平面,求证:;
【小试牛刀】
1. 如图,在正方体中,E为的中点.
求证:平面;
2. 如图,在正方体中,是棱的中点.
证明:平面;
3. 如图,在三棱柱中,侧面⊥底面,,,分别为棱的中点.
(1)求三棱柱的体积;
(2)在直线上是否存在一点,使得平面 若存在,求出的长,若不存在,说明理由.
【巩固练习】
如图,在四棱锥中,侧面是等边三角形,且平面平面,为的中点,
求证:平面;
2. 如图,在三棱柱中,底面,,点是的中点.
求证:平面.
3.如图,在四棱锥中,底面是平行四边形,,侧面底面,,,分别为的中点,点在线段上.
求证:平面
4. 如图,在四棱锥中,底面是正方形.点是棱的中点,平面与棱交于点.
求证:∥;
5. 如图,在四棱锥中,,,,,,.
若为的中点,求证:平面
【课后拾遗】
20
21
【课前诊断】
成绩(满分10): 完成情况: 优/中/差
1. 已知是两条异面直线,那么与的位置关系__________.
2. 判断正误
(1)两个不重合的平面只能把空间分成四个部分
(2)两个平面有一个公共点,就说相交于点,记作
(3)两两相交的三条直线最多可以确定三个平面
(4)如果两个平面有三个公共点,则这两个平面重合
3. 如图所示,在正方体中,分别是的中点.
求证:(1)四点共面;
(2)三线共点.
【知识点:空间中直线、平面的平行关系】
一、空间中平行
定义 图形 判定定理 性质定理 符号语言
线线平行 同一平面内无公共点的两条直线平行 平面几何、立体几何中有关的判定定理 空间中平行于同一直线的两直线平行
线面平行 若直线和平面无公共点,则称直线和平面平行 平面外一条直线与此平面内一条直线平行,则该直线与此平面平行 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线和该直线平行 判定 性质
面面平行 若两个平面无公共点,则称这两个平面平行 一个平面内的两条相交直线与另一平面平行,则这两个平面平行 如果两个平行平面同时和第三个平面相交,那么它们的交线平行 判定性质
二、两平面平行的性质定理
文字语言 图形语言 符号语言
性质定理1 如果两个平面平行,那么在一个平面内的所有直线都平行于另一个平面 且
性质定理2 如果两个平行平面中有一个平面垂直于一条直线,那么另一个平面也垂直于这条直线 且
三、线线平行、线面平行、面面平行间的关系
由于三者之间相互沟通、相互联系,因此立体几何问题的解决往往可以一题多解(证).
【典型例题】
考点一:空间中直线与平面的平行
题型一:直接法
例1. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面底面ABCD,E为侧棱PD上一点.求证:平面
求证:平面ABE;
【答案】
题型二:平四法
例2. 如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△的位置,使得平面平面,为的中点,如图2.
求证:平面;
例3. 如图所示,在四棱锥中,,,是的中点.
求证:平面.
例2(20年大兴高三期末)如图,在四棱锥C﹣ABEF中,平面ABEF⊥平面ABC,△ABC是边长2的等边三角形,AB∥EF,∠ABE=90°,BE=EF=1,点M为BC的中点.
求证:EM∥平面ACF;
】
练2-1(20年门头沟一模)在四棱锥的底面中,,是的中点,且,求证:;
题型三:中位线法
例1(20年海淀高三期末)如图,在三棱锥中,平面平面,和均是等腰直角三角形,,,,分别为, 的中点.
求证:平面;
练1(20年适应性测试)如图,在四棱锥中,,,,底面为正方形,分别为的中点.
(Ⅰ)求证:平面;
练2. 如图,四棱锥的底面是正方形,侧棱底面,E是的中点.
(1)求证:平面;
(2)求证:平面;
练1-1 (20年西城高三期末)如图,在三棱柱中,平面,为正三角形,侧面是边长为2的正方形,为的中点.
(I)求证:平面;
练3. 如图,在四棱锥中,底面是菱形,,平面,,,.
求证:直线平面PNC;
题型四:构造面面平行法
例3(2020北京十一学校高一下期末)如图,四棱锥中,,,分别为线段的中点,与交于点,是线段上的一点,求证:平面
练习3-1(2020北京101中学高一下期末)如图,三棱柱中,分别为中点,求证:平面
练习3-2(2016-2017房山高三理二模17)如图,正方形与梯形所在的平面互相垂直,已知,,
.
(Ⅰ)求证:平面;
考点二:空间中平面与平面的平行
例1. 如图,已知正方形所在平面和平行四边形所在平面互相垂直,平面平面,,是线段上的一点且平面.
求证:平面平面;
练1.(10-11海淀二模)
已知直三棱柱的所有棱长都相等,且分别为的中点.求证:平面平面;
练1. 如图,在多面体中,底面是边长为的正方形,四边形是矩形,平面平面,,和分别是和的中点.
求证:平面平面
例1.(2013-2014北大附检测)如图,为所在平面外一点,分别为的重心.求证:平面平面
考点三:空间中直线与直线的平行
例1. 如图所示,在四棱锥中,平面, ,是的中点.
求证:
例2. 在四棱锥中,底面为直角梯形,,,,为线段的中点. 底面,点是棱的中点,平面与棱相交于点.
求证:;
练1. 如图,正方形 的边长为2,分别为的中点,在五棱锥中,为棱的中点,平面与棱分别交于点.
求证:
练1. 如图,在四棱锥中,已知底面为平行四边形,点为棱的中点.
(1)求证:平面;
(2)设平面平面,点在上,求证:为的中点.
练2. 四棱锥,,平面,设平面平面,求证:;
【小试牛刀】
1. 如图,在正方体中,E为的中点.
求证:平面;
2. 如图,在正方体中,是棱的中点.
证明:平面;
3. 如图,在三棱柱中,侧面⊥底面,,,分别为棱的中点.
(1)求三棱柱的体积;
(2)在直线上是否存在一点,使得平面 若存在,求出的长,若不存在,说明理由.
【巩固练习】
如图,在四棱锥中,侧面是等边三角形,且平面平面,为的中点,
求证:平面;
2. 如图,在三棱柱中,底面,,点是的中点.
求证:平面.
3.如图,在四棱锥中,底面是平行四边形,,侧面底面,,,分别为的中点,点在线段上.
求证:平面
4. 如图,在四棱锥中,底面是正方形.点是棱的中点,平面与棱交于点.
求证:∥;
5. 如图,在四棱锥中,,,,,,.
若为的中点,求证:平面
【课后拾遗】
20
21
