2021-2022学年人教版七年级数学下册5.1.3同位角、内错角、同旁内角 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1.3同位角、内错角、同旁内角 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 672.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 11:38:30 | ||
图片预览


文档简介
(共21张PPT)
5.1 相交线
第五章 相交线与平行线
5.1.3 同位角、内错角、同旁内角
1
2
3
4
5
6
7
8
A
B
C
D
E
F
7
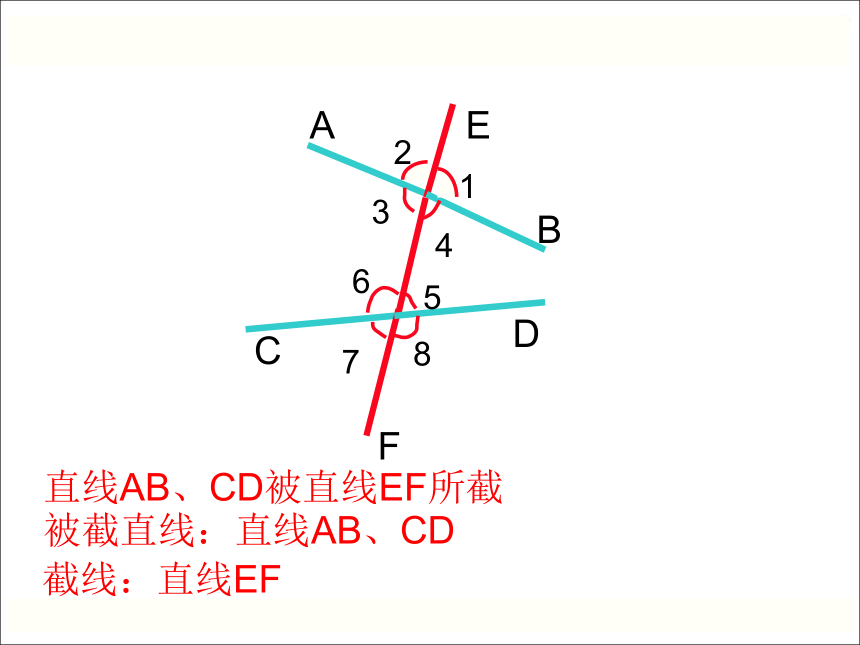
直线AB、CD被直线EF所截
被截直线:直线AB、CD
截线:直线EF
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
7
B
C
A
A
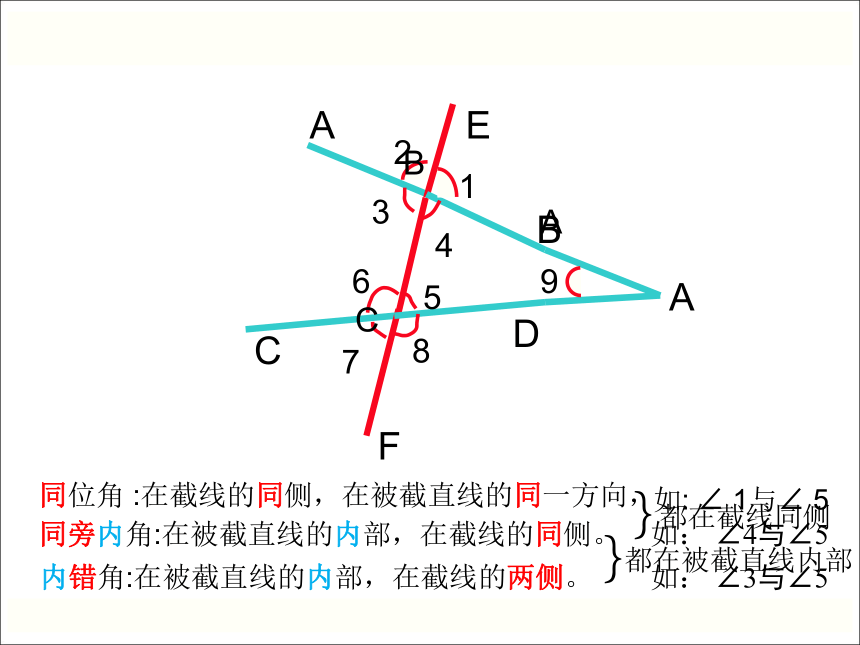
同位角 :在截线的同侧,在被截直线的同一方向,
同旁内角:在被截直线的内部,在截线的同侧。
内错角:在被截直线的内部,在截线的两侧。
如: ∠ 1与∠ 5
如: ∠4与∠5
如: ∠3与∠5
}
}
都在截线同侧
都在被截直线内部
1
2
3
4
5
6
7
8
D
A
C
E
F
7
B
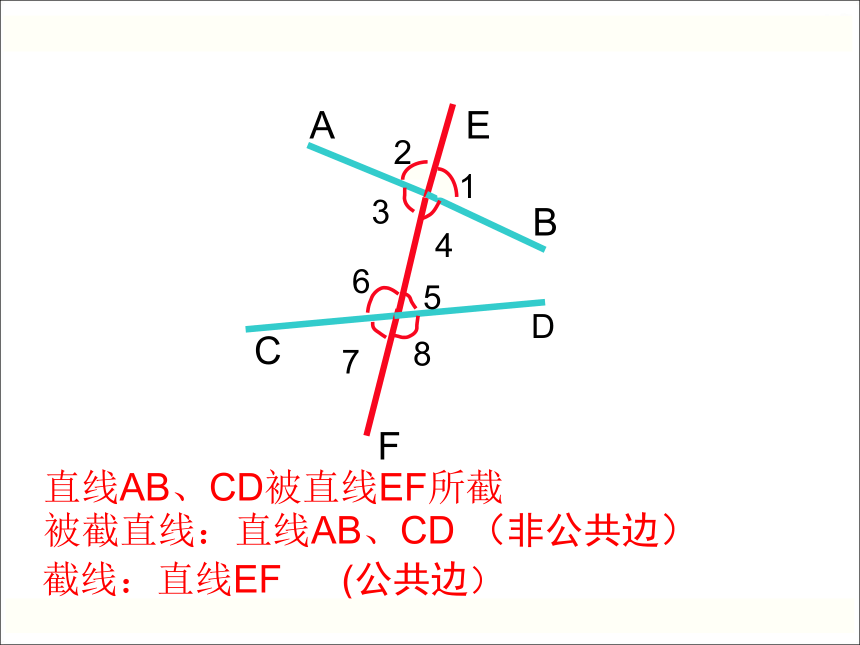
直线AB、CD被直线EF所截
被截直线:直线AB、CD
截线:直线EF
(公共边)
(非公共边)
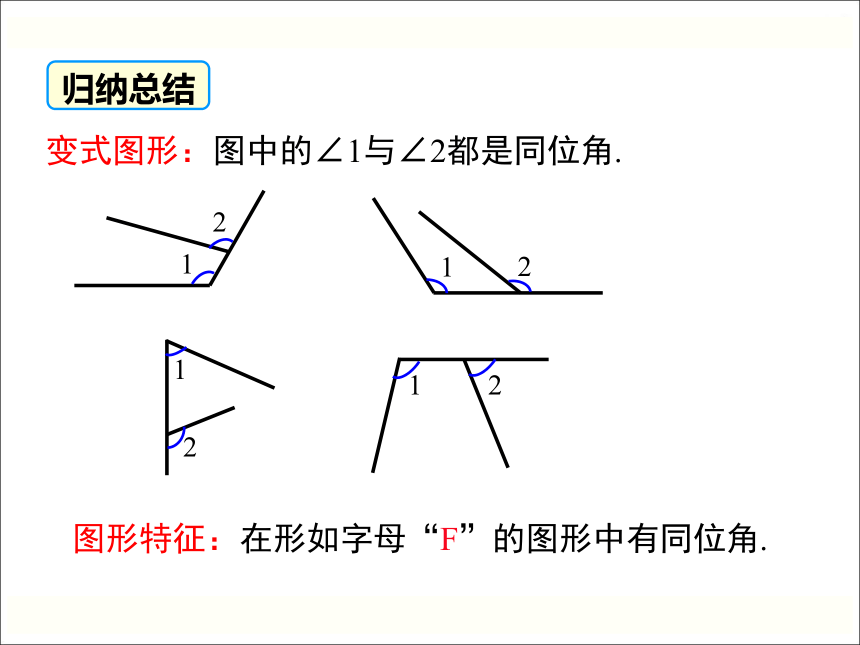
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
A
A.(1),(2) B.(3),(4)
C.(1),(2),(3) D.(2),(3) ,(3)
例1 下列图形中,∠1和∠2是同位角的有( )
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
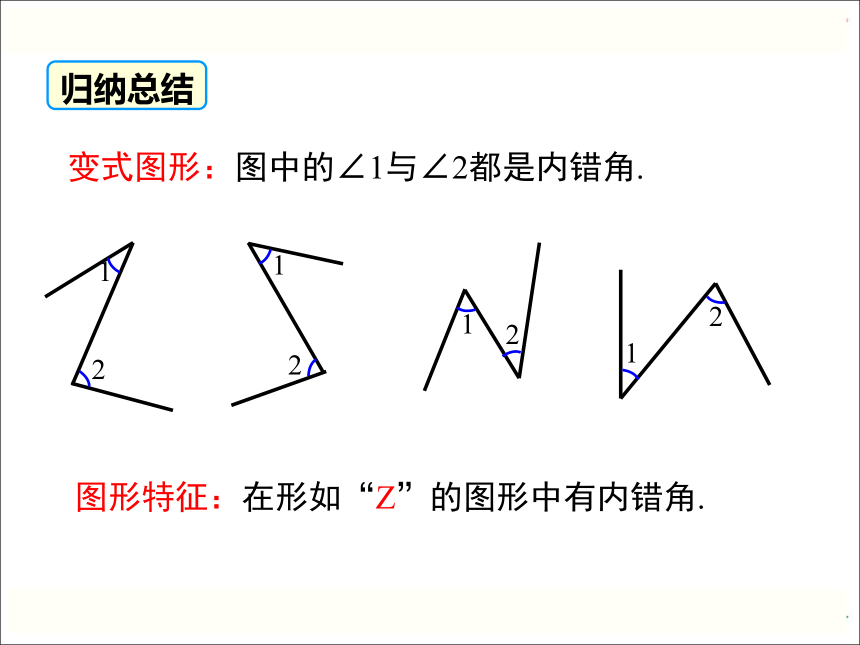
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
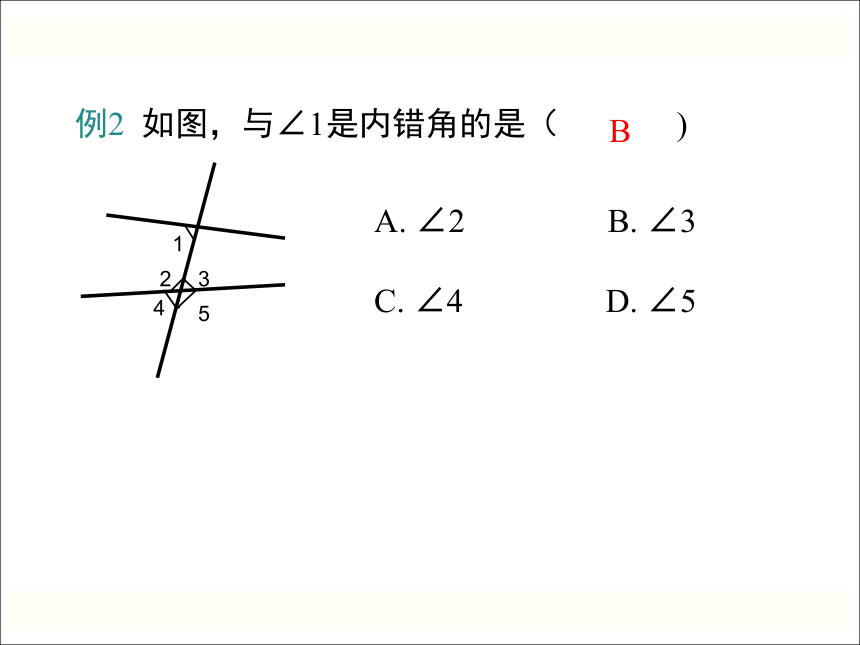
例2 如图,与∠1是内错角的是( )
1
3
2
4
5
A. ∠2 B. ∠3
C. ∠4 D. ∠5
B
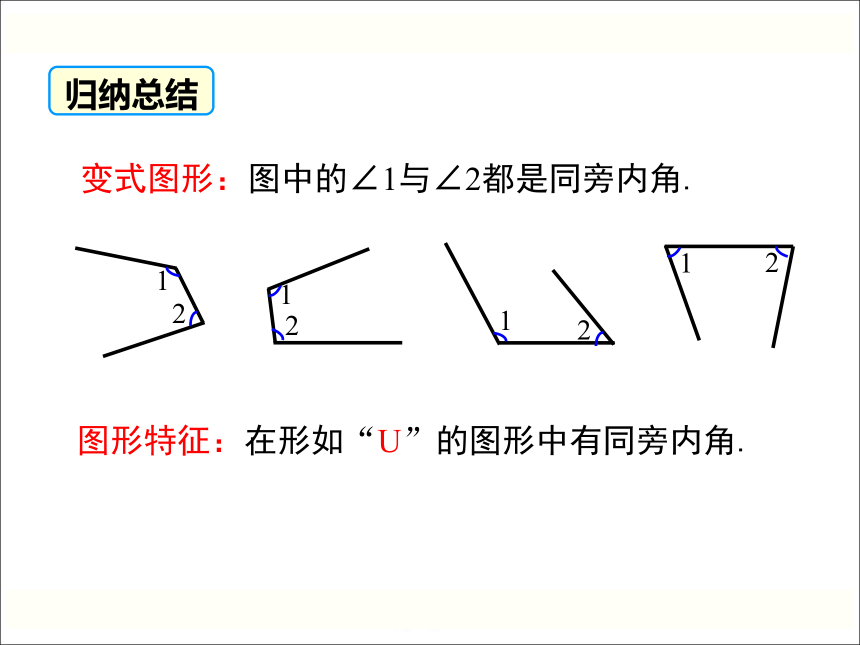
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
例3 下列图形中,∠1和∠2是同旁内角的有( )
1
1
A
B
C
D
1
2
2
2
1
2
A
识别这些角是同位角、内错角还是同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
耍耍你的小聪明(抢答):
例4 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6;同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
典例精析
练一练:∠A与∠8是哪两条直线被哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
1.如图,∠1和∠B的位置关系是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
练一练
1
当堂练习
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角;
3.看图填空:
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角;
∠4
图1
图2
(3)如图3,∠1与∠3是AB和AF被_____所截构成的 角;
DE
内错
(4)如图4,∠2与∠4是 和 被BC所截构成的____角.
AB
AF
同位
图3
图4
4.如图:∠1与∠2,∠3与∠4各是哪两条直线被哪条直
线所截形成的 它们各是什么关系的角
A
B
C
D
A
B
C
D
E
(1)
(2)
1
2
4
3
1
3
2
4
(1)、∠1与∠2是直线AB,CD被直线AD所截形成的; 是内错角。
∠3与∠4是直线AC,BD被直线AD所截形成的; 是内错角。
(2)、∠1与∠2是直线AB,CD被直线CB所截形成的; 是同旁内角。
∠3与∠4是直线AC,BD被直线CE所截形成的; 是同位角。
5.根据地图填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法(描图法,定义法):
方法一:①把两个角在图中描画出来;
②观察所描的角,判断所属“字母”类型,
同位角为“F”型;内错角为“Z”型;同旁内角为“U”
型;注意图形的变式(旋转、对称)也是符合的.
课堂小结
方法二:找到两个角的公共直线(即:截线);找到
两个角的另一边(即:被截直线)(非公共
边),再根据各种角的位置特点找。
课后作业
课后作业:同步训练6-8页,
本节相应练习。
5.1 相交线
第五章 相交线与平行线
5.1.3 同位角、内错角、同旁内角
1
2
3
4
5
6
7
8
A
B
C
D
E
F
7
直线AB、CD被直线EF所截
被截直线:直线AB、CD
截线:直线EF
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
7
B
C
A
A
同位角 :在截线的同侧,在被截直线的同一方向,
同旁内角:在被截直线的内部,在截线的同侧。
内错角:在被截直线的内部,在截线的两侧。
如: ∠ 1与∠ 5
如: ∠4与∠5
如: ∠3与∠5
}
}
都在截线同侧
都在被截直线内部
1
2
3
4
5
6
7
8
D
A
C
E
F
7
B
直线AB、CD被直线EF所截
被截直线:直线AB、CD
截线:直线EF
(公共边)
(非公共边)
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
A
A.(1),(2) B.(3),(4)
C.(1),(2),(3) D.(2),(3) ,(3)
例1 下列图形中,∠1和∠2是同位角的有( )
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
例2 如图,与∠1是内错角的是( )
1
3
2
4
5
A. ∠2 B. ∠3
C. ∠4 D. ∠5
B
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
例3 下列图形中,∠1和∠2是同旁内角的有( )
1
1
A
B
C
D
1
2
2
2
1
2
A
识别这些角是同位角、内错角还是同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
耍耍你的小聪明(抢答):
例4 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6;同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
典例精析
练一练:∠A与∠8是哪两条直线被哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
1.如图,∠1和∠B的位置关系是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
练一练
1
当堂练习
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角;
3.看图填空:
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角;
∠4
图1
图2
(3)如图3,∠1与∠3是AB和AF被_____所截构成的 角;
DE
内错
(4)如图4,∠2与∠4是 和 被BC所截构成的____角.
AB
AF
同位
图3
图4
4.如图:∠1与∠2,∠3与∠4各是哪两条直线被哪条直
线所截形成的 它们各是什么关系的角
A
B
C
D
A
B
C
D
E
(1)
(2)
1
2
4
3
1
3
2
4
(1)、∠1与∠2是直线AB,CD被直线AD所截形成的; 是内错角。
∠3与∠4是直线AC,BD被直线AD所截形成的; 是内错角。
(2)、∠1与∠2是直线AB,CD被直线CB所截形成的; 是同旁内角。
∠3与∠4是直线AC,BD被直线CE所截形成的; 是同位角。
5.根据地图填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法(描图法,定义法):
方法一:①把两个角在图中描画出来;
②观察所描的角,判断所属“字母”类型,
同位角为“F”型;内错角为“Z”型;同旁内角为“U”
型;注意图形的变式(旋转、对称)也是符合的.
课堂小结
方法二:找到两个角的公共直线(即:截线);找到
两个角的另一边(即:被截直线)(非公共
边),再根据各种角的位置特点找。
课后作业
课后作业:同步训练6-8页,
本节相应练习。
