《数学广角-鸽巢问题》课件 数学六年级下册(共30张PPT)人教版
文档属性
| 名称 | 《数学广角-鸽巢问题》课件 数学六年级下册(共30张PPT)人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-31 23:37:58 | ||
图片预览





文档简介
(共30张PPT)
数学广角-鸽巢问题
一副扑克牌,取出大小王,5位同学每人随意抽出一张。
至少有2张牌是同花色的
活动内容: 将4支铅笔放进3个笔筒里。
活动目的: 无论怎样放,
总有一个笔筒里至少有( )支笔。
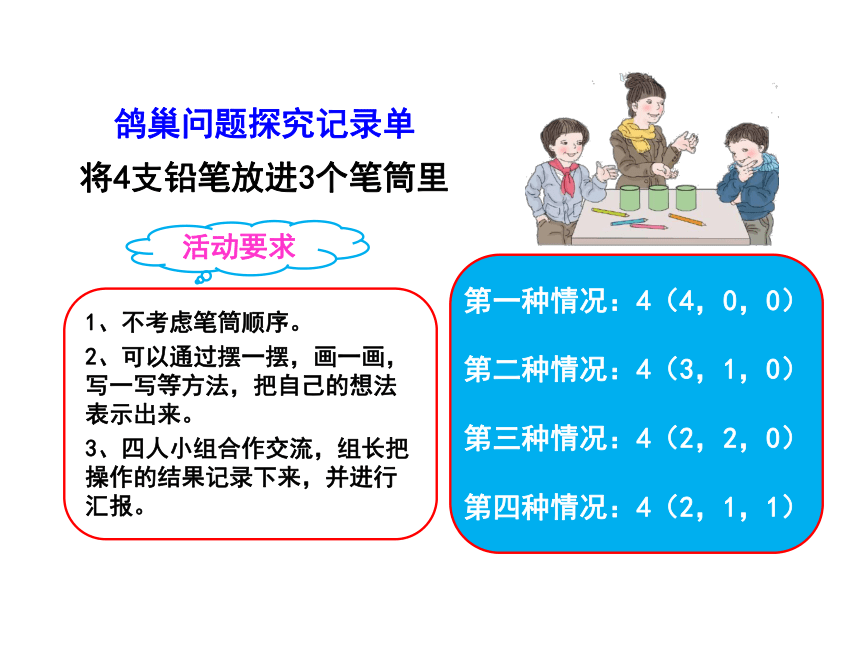
鸽巢问题探究记录单
将4支铅笔放进3个笔筒里
第一种情况:4(4,0,0)
第二种情况:4(3,1,0)
第三种情况:4(2,2,0)
第四种情况:4(2,1,1)
1、不考虑笔筒顺序。
2、可以通过摆一摆,画一画,写一写等方法,把自己的想法表示出来。
3、四人小组合作交流,组长把操作的结果记录下来,并进行汇报。
活动要求
第一种情况:把4支笔都放在一个笔筒里。
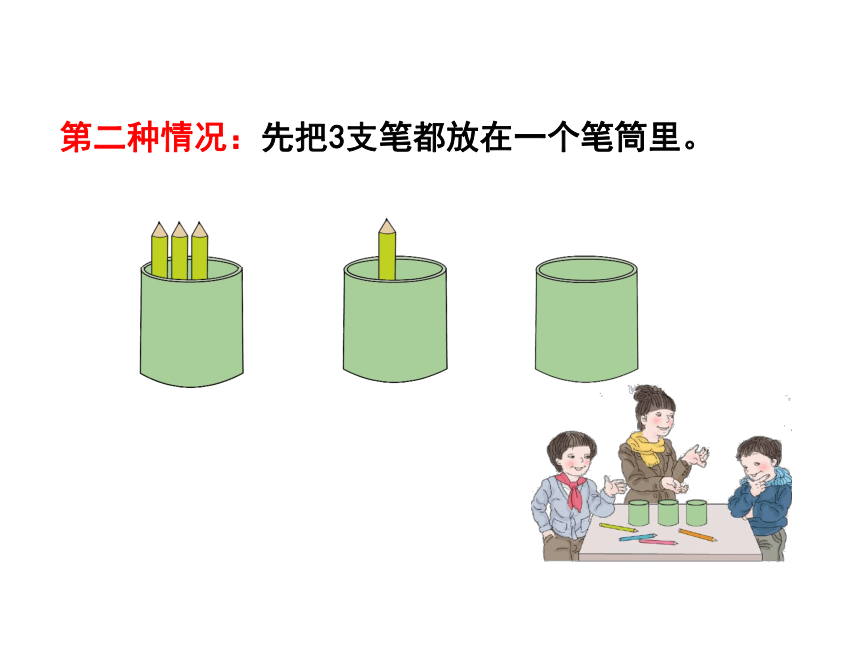
第二种情况:先把3支笔都放在一个笔筒里。
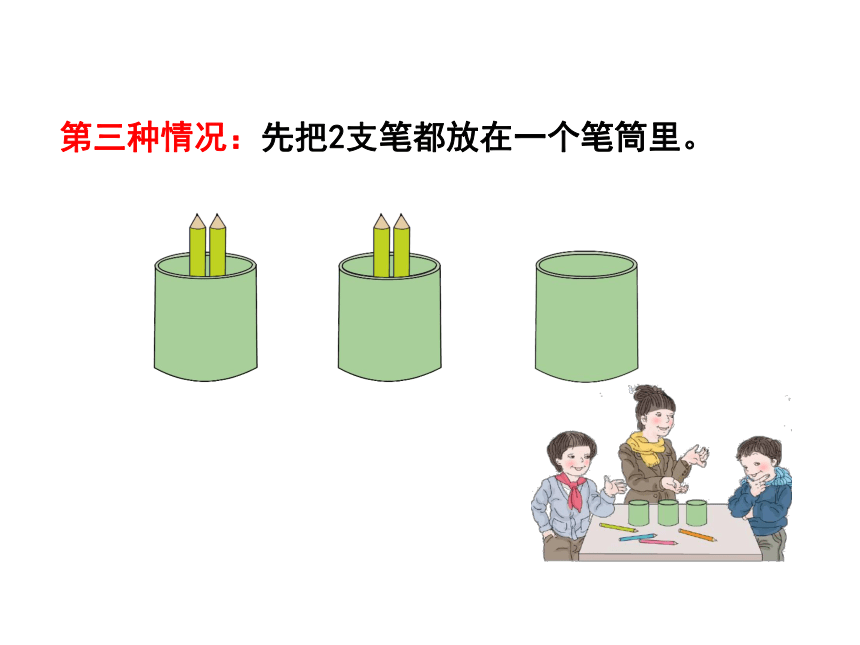
第三种情况:先把2支笔都放在一个笔筒里。
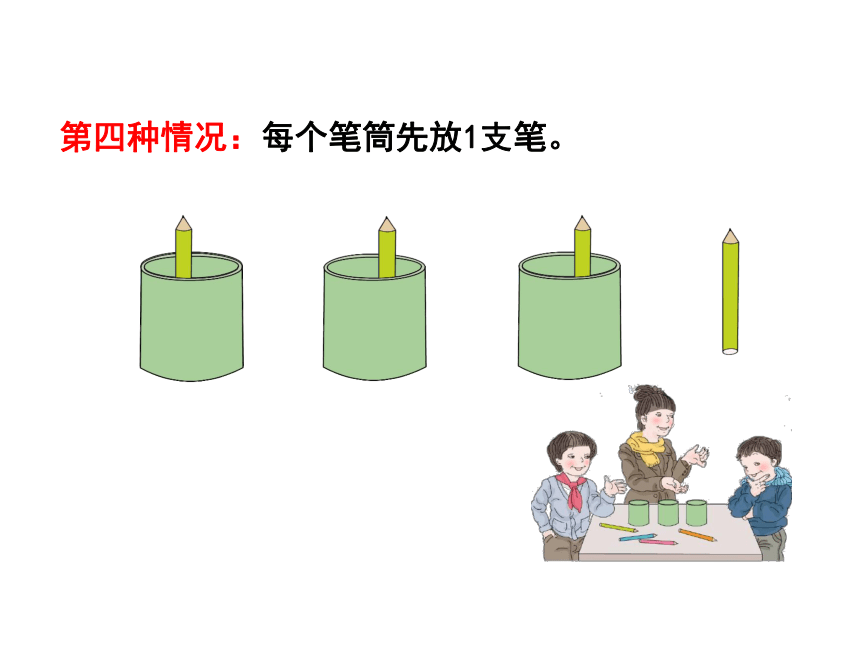
第四种情况:每个笔筒先放1支笔。
无论怎么放,
总有一个笔筒里
至少放进2支笔。
枚举法
怎样才能最快地知道这个放得最多的笔筒里
至少有几支笔?
先平均分
从最不利的情况考虑,
先放入相同的最多数。
假设每个笔筒里先放1支铅笔,最多放3支,剩下的1支无论放进哪个笔筒里,总有一个笔筒里至少放2支笔。
假设法说理
4只鸽子飞回3个鸽巢,总有一个鸽巢至少飞进( )只鸽子。
鸽巢问题
把5支笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
假设每个笔筒里先放1支笔,最多可放4支,剩下的1支还要放进其中一个笔筒里,不管怎么放,
总有一个笔筒里至少放进( 2 )支笔。
我能说
把6支笔放进5个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
我能说
假设每个笔筒里先放1支笔,最多可放5支,剩下的1支还要放进其中一个笔筒里,不管怎么放,
总有一个笔筒里至少放进( 2 )支笔。
把10支笔放进9个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
我能说
把 4 支笔放进 3 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 5 支笔放进 4 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 6 支笔放进 5 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 10 支笔放进 9 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
n+1
n
把n+1个物体放进n个抽屉里,不管怎么放,
总有一个抽屉里至少放进2个物体。
我的发现
一副扑克牌,取出大小王,5位同学每人随意抽出一张。
至少有2张牌是同花色的
例2.把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进( )本书。为什么?
7÷3 = 2
……
1
2+1 = 3
8本呢?
8÷3 = 2
……
2
2+1 = 3
10本呢?
10÷3 = 3
……
1
3+1 = 4
铅笔
物体数÷抽屉数 = 商
……
余数
至少数 = 商 + 1
笔筒
鸽子
鸽巢
书本
抽屉
铅笔
装东西的
被装的
被装的÷装东西的 = 商
……
余数
随意找13位老师,他们中至少有几个人的属相相同?为什么?
13÷12=1
……
1
1+1 = 2
12个抽屉
12个属相
13个物体
13个人
1、5个人坐4把椅子,总有一把椅子至少坐2人,为什么?
5÷4 = 1
……
1
1+1 = 2
基本练习
2、7只鸽子飞回5个鸽巢,至少有( )只鸽子要飞进同一个鸽巢里。
7÷5 = 1
……
2
1+1 = 2
基本练习
3、11只鸽子飞回4个鸽巢,总有一个鸽巢至少飞进了( )只鸽子。
11÷4 = 2
……
3
2+1 = 3
基本练习
数学书第68页——69页。
解答鸽巢问题的关键是什么?
找准哪个是物体,也就是被装的;哪个是抽屉,也就是装东西的。以及他们的个数。
有余数时:
物体数÷抽屉数 = 商
……
余数
至少数 = 商 + 1
无余数时:
物体数÷抽屉数 = 商
至少数 = 商
1、从马路上随意找25个人,他们中至少有( )个人的属相相同。
课堂过关练习
2、从电影院随意找24个人,他们中至少有( )个人的生日在同一个月。
3、向东小学六年级共有367名学生,六年级里至少有( )个人的生日在同一天。
谈谈鸽巢问题(抽屉原理)你的收获
数学方法
数学思想
1、枚举法 2、假设法
1、数形结合 2、数学建模
早在我国古代,就有不少成功运用抽屉原理来分析问题的例子。例如:宋代费衮(gun)的《梁谿(xi)漫志》中,就曾运用抽屉原理来批驳“算命”一类活动的谬论。然而,令人不无遗憾的是:我国学者虽然很早就会用抽屉原理来分析问题,但没有关于抽屉原理的概括性文字,没有人将他抽象为一条普通原理,最后还不得不将这一原理冠以数百年以后西方学者狄利克雷的名字。
本节课结束
同学们,再见!
数学广角-鸽巢问题
一副扑克牌,取出大小王,5位同学每人随意抽出一张。
至少有2张牌是同花色的
活动内容: 将4支铅笔放进3个笔筒里。
活动目的: 无论怎样放,
总有一个笔筒里至少有( )支笔。
鸽巢问题探究记录单
将4支铅笔放进3个笔筒里
第一种情况:4(4,0,0)
第二种情况:4(3,1,0)
第三种情况:4(2,2,0)
第四种情况:4(2,1,1)
1、不考虑笔筒顺序。
2、可以通过摆一摆,画一画,写一写等方法,把自己的想法表示出来。
3、四人小组合作交流,组长把操作的结果记录下来,并进行汇报。
活动要求
第一种情况:把4支笔都放在一个笔筒里。
第二种情况:先把3支笔都放在一个笔筒里。
第三种情况:先把2支笔都放在一个笔筒里。
第四种情况:每个笔筒先放1支笔。
无论怎么放,
总有一个笔筒里
至少放进2支笔。
枚举法
怎样才能最快地知道这个放得最多的笔筒里
至少有几支笔?
先平均分
从最不利的情况考虑,
先放入相同的最多数。
假设每个笔筒里先放1支铅笔,最多放3支,剩下的1支无论放进哪个笔筒里,总有一个笔筒里至少放2支笔。
假设法说理
4只鸽子飞回3个鸽巢,总有一个鸽巢至少飞进( )只鸽子。
鸽巢问题
把5支笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
假设每个笔筒里先放1支笔,最多可放4支,剩下的1支还要放进其中一个笔筒里,不管怎么放,
总有一个笔筒里至少放进( 2 )支笔。
我能说
把6支笔放进5个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
我能说
假设每个笔筒里先放1支笔,最多可放5支,剩下的1支还要放进其中一个笔筒里,不管怎么放,
总有一个笔筒里至少放进( 2 )支笔。
把10支笔放进9个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
我能说
把 4 支笔放进 3 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 5 支笔放进 4 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 6 支笔放进 5 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 10 支笔放进 9 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
n+1
n
把n+1个物体放进n个抽屉里,不管怎么放,
总有一个抽屉里至少放进2个物体。
我的发现
一副扑克牌,取出大小王,5位同学每人随意抽出一张。
至少有2张牌是同花色的
例2.把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进( )本书。为什么?
7÷3 = 2
……
1
2+1 = 3
8本呢?
8÷3 = 2
……
2
2+1 = 3
10本呢?
10÷3 = 3
……
1
3+1 = 4
铅笔
物体数÷抽屉数 = 商
……
余数
至少数 = 商 + 1
笔筒
鸽子
鸽巢
书本
抽屉
铅笔
装东西的
被装的
被装的÷装东西的 = 商
……
余数
随意找13位老师,他们中至少有几个人的属相相同?为什么?
13÷12=1
……
1
1+1 = 2
12个抽屉
12个属相
13个物体
13个人
1、5个人坐4把椅子,总有一把椅子至少坐2人,为什么?
5÷4 = 1
……
1
1+1 = 2
基本练习
2、7只鸽子飞回5个鸽巢,至少有( )只鸽子要飞进同一个鸽巢里。
7÷5 = 1
……
2
1+1 = 2
基本练习
3、11只鸽子飞回4个鸽巢,总有一个鸽巢至少飞进了( )只鸽子。
11÷4 = 2
……
3
2+1 = 3
基本练习
数学书第68页——69页。
解答鸽巢问题的关键是什么?
找准哪个是物体,也就是被装的;哪个是抽屉,也就是装东西的。以及他们的个数。
有余数时:
物体数÷抽屉数 = 商
……
余数
至少数 = 商 + 1
无余数时:
物体数÷抽屉数 = 商
至少数 = 商
1、从马路上随意找25个人,他们中至少有( )个人的属相相同。
课堂过关练习
2、从电影院随意找24个人,他们中至少有( )个人的生日在同一个月。
3、向东小学六年级共有367名学生,六年级里至少有( )个人的生日在同一天。
谈谈鸽巢问题(抽屉原理)你的收获
数学方法
数学思想
1、枚举法 2、假设法
1、数形结合 2、数学建模
早在我国古代,就有不少成功运用抽屉原理来分析问题的例子。例如:宋代费衮(gun)的《梁谿(xi)漫志》中,就曾运用抽屉原理来批驳“算命”一类活动的谬论。然而,令人不无遗憾的是:我国学者虽然很早就会用抽屉原理来分析问题,但没有关于抽屉原理的概括性文字,没有人将他抽象为一条普通原理,最后还不得不将这一原理冠以数百年以后西方学者狄利克雷的名字。
本节课结束
同学们,再见!
