人教版数学七年级下册 5.2.1 平行线的判定 练习(word版含答案)
文档属性
| 名称 | 人教版数学七年级下册 5.2.1 平行线的判定 练习(word版含答案) | 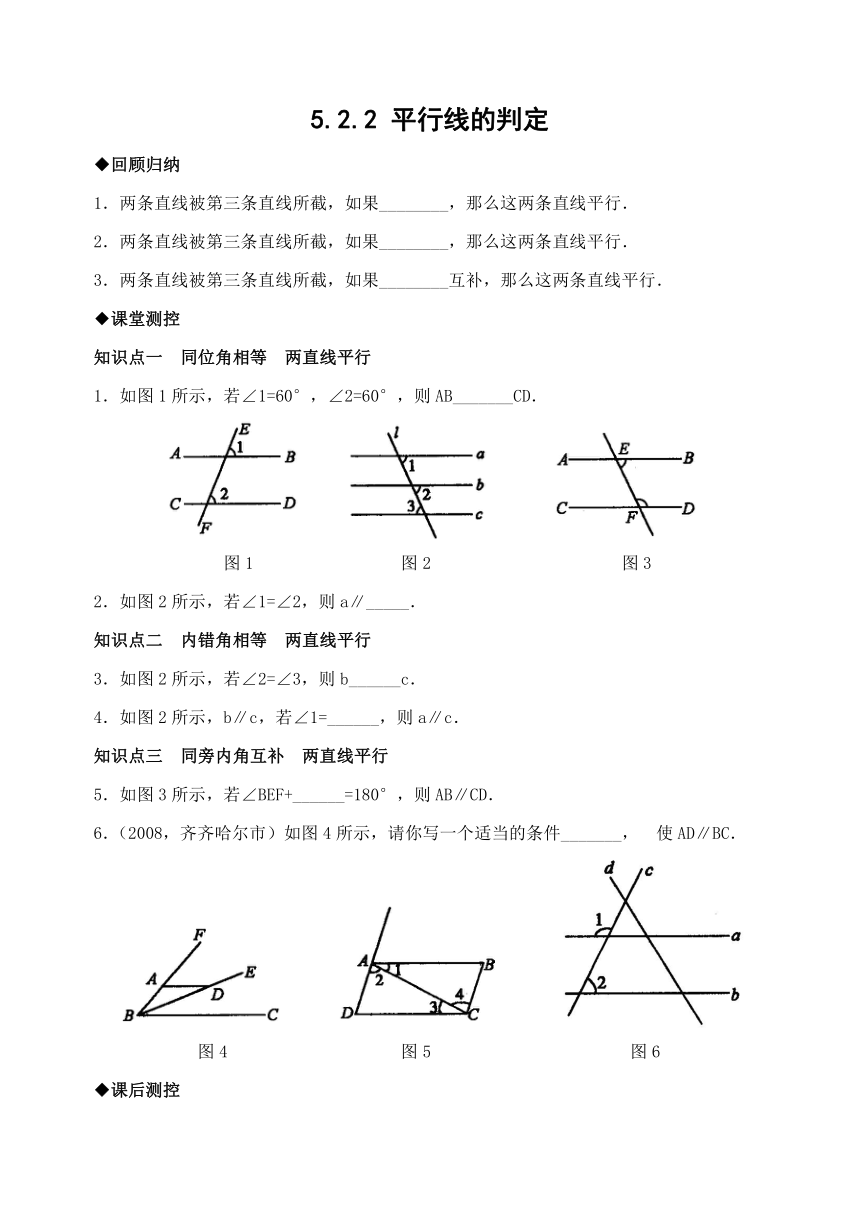 | |
| 格式 | doc | ||
| 文件大小 | 53.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 08:11:13 | ||
图片预览

文档简介
5.2.2 平行线的判定
◆回顾归纳
1.两条直线被第三条直线所截,如果________,那么这两条直线平行.
2.两条直线被第三条直线所截,如果________,那么这两条直线平行.
3.两条直线被第三条直线所截,如果________互补,那么这两条直线平行.
◆课堂测控
知识点一 同位角相等 两直线平行
1.如图1所示,若∠1=60°,∠2=60°,则AB_______CD.
图1 图2 图3
2.如图2所示,若∠1=∠2,则a∥_____.
知识点二 内错角相等 两直线平行
3.如图2所示,若∠2=∠3,则b______c.
4.如图2所示,b∥c,若∠1=______,则a∥c.
知识点三 同旁内角互补 两直线平行
5.如图3所示,若∠BEF+______=180°,则AB∥CD.
6.(2008,齐齐哈尔市)如图4所示,请你写一个适当的条件_______, 使AD∥BC.
图4 图5 图6
◆课后测控
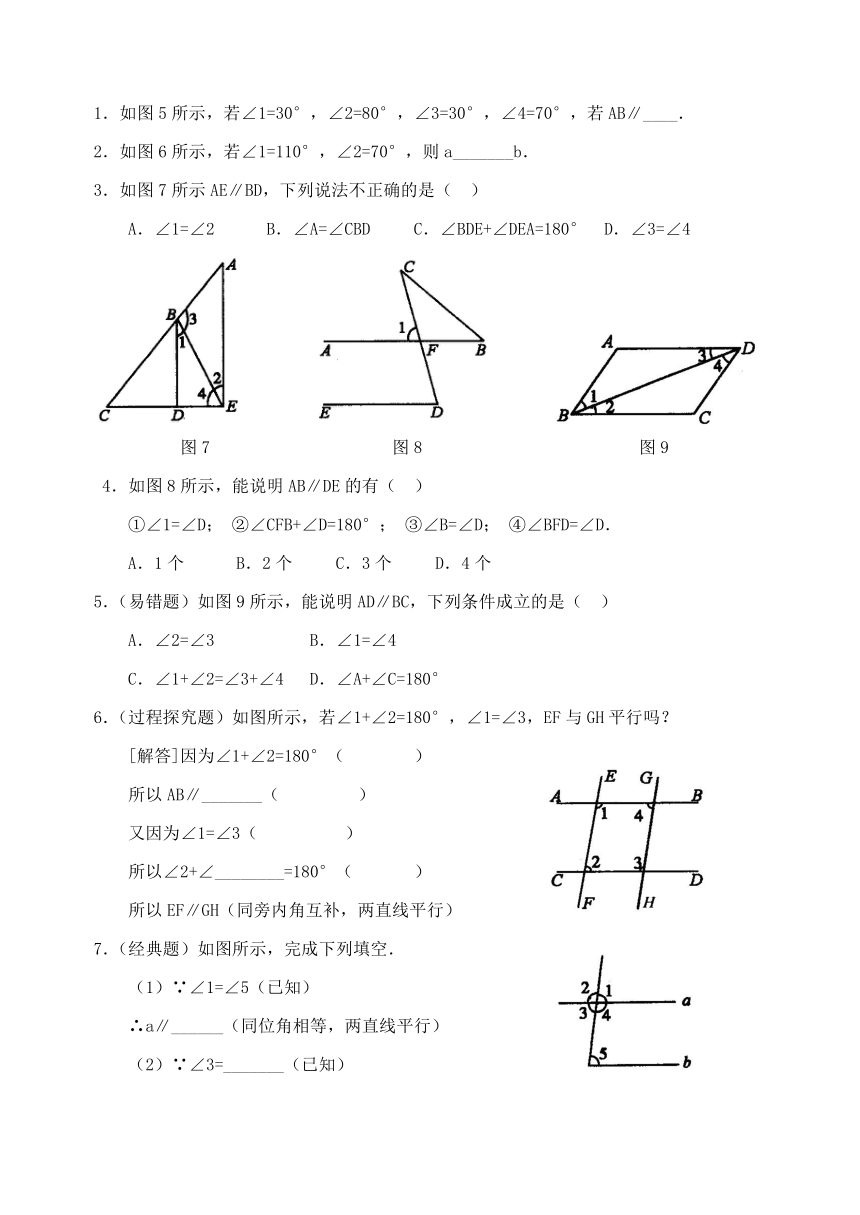
1.如图5所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
2.如图6所示,若∠1=110°,∠2=70°,则a_______b.
3.如图7所示AE∥BD,下列说法不正确的是( )
A.∠1=∠2 B.∠A=∠CBD C.∠BDE+∠DEA=180° D.∠3=∠4
图7 图8 图9
4.如图8所示,能说明AB∥DE的有( )
①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
5.(易错题)如图9所示,能说明AD∥BC,下列条件成立的是( )
A.∠2=∠3 B.∠1=∠4
C.∠1+∠2=∠3+∠4 D.∠A+∠C=180°
6.(过程探究题)如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?
[解答]因为∠1+∠2=180°( )
所以AB∥_______( )
又因为∠1=∠3( )
所以∠2+∠________=180°( )
所以EF∥GH(同旁内角互补,两直线平行)
7.(经典题)如图所示,完成下列填空.
(1)∵∠1=∠5(已知)
∴a∥______(同位角相等,两直线平行)
(2)∵∠3=_______(已知)
∴a∥b(内错角相等,两直线平行)
(3)∵∠5+_______=180°(已知)
∴______∥_______(同旁内角互补,两直线平行)
8.(原创题)如图所示,写出所有角满足的条件使AB∥EF,并说明理由.
◆拓展创新
9.(应用题)(1)如图(1)所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.
判断AB与CD的位置关系,并说明理由;
(2)如图(2)所示在(1)的条件下,若小路OM平分∠EOB.通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N位置关系.
答案:
回顾归纳
1.同位角相等 2.内错角相等 3.同旁内角
课堂测控
1.∥ 2.b 3.∥ 4.∠2或∠3 5.∠EFD
6.∠ABC+∠BAD=180°或∠ADB=∠DBC或∠FAD=∠ABC.(任选一个即可).
解题规律:依照三个判定定理,同位角,内错角,同旁内角关系判定两直线平行.
课后测控
1.CD 2.∥ 3.D 4.C(点拨:①②④正确)
5.A(点拨:∠1=∠4得AB∥CD,∠1+∠2≠∠3+∠4,∠A+∠C≠180°)
6.已知,CD,同旁内角互补两直线平行,已知,∠3,等量代换
解题规律:EF∥GH成立→∠2+∠3=180°,又∠1=∠3,∴∠1+∠2=180°(已知)
7.(1)b (2)∠5 (3)∠4,a,b
思路点拨:由条件与结论关系及括号中定理判断填空内容.
8.①同位角∠A=∠CEF,∠B=∠EFC,
②内错角∠ADE=∠DEF,
③同旁内角.∠A+∠AEF=180°,∠B+∠BFE=180°,∠BDE+∠DEF=180°
思路点拨:AB,EF被AC所截,AB,EF被BC所截,AB,EF被DE所截,三个方面的关系中存在同位角,内错角,同旁内角来判定AB∥EF的条件.
9.(1)∵AB⊥EF,CD⊥EF
∴AB∥CD(两条直线都垂直于同一条直线,这两条直线平行)
(2)延长NO′至P,可证∠EOM=∠EO′P=45°,得OM∥O′N.
解题技巧:(1)中由垂线定义及平行线判定推理来证,
(2)中要作辅助线延长NO′至P,运用同位角相等来证明.
◆回顾归纳
1.两条直线被第三条直线所截,如果________,那么这两条直线平行.
2.两条直线被第三条直线所截,如果________,那么这两条直线平行.
3.两条直线被第三条直线所截,如果________互补,那么这两条直线平行.
◆课堂测控
知识点一 同位角相等 两直线平行
1.如图1所示,若∠1=60°,∠2=60°,则AB_______CD.
图1 图2 图3
2.如图2所示,若∠1=∠2,则a∥_____.
知识点二 内错角相等 两直线平行
3.如图2所示,若∠2=∠3,则b______c.
4.如图2所示,b∥c,若∠1=______,则a∥c.
知识点三 同旁内角互补 两直线平行
5.如图3所示,若∠BEF+______=180°,则AB∥CD.
6.(2008,齐齐哈尔市)如图4所示,请你写一个适当的条件_______, 使AD∥BC.
图4 图5 图6
◆课后测控
1.如图5所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
2.如图6所示,若∠1=110°,∠2=70°,则a_______b.
3.如图7所示AE∥BD,下列说法不正确的是( )
A.∠1=∠2 B.∠A=∠CBD C.∠BDE+∠DEA=180° D.∠3=∠4
图7 图8 图9
4.如图8所示,能说明AB∥DE的有( )
①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
5.(易错题)如图9所示,能说明AD∥BC,下列条件成立的是( )
A.∠2=∠3 B.∠1=∠4
C.∠1+∠2=∠3+∠4 D.∠A+∠C=180°
6.(过程探究题)如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?
[解答]因为∠1+∠2=180°( )
所以AB∥_______( )
又因为∠1=∠3( )
所以∠2+∠________=180°( )
所以EF∥GH(同旁内角互补,两直线平行)
7.(经典题)如图所示,完成下列填空.
(1)∵∠1=∠5(已知)
∴a∥______(同位角相等,两直线平行)
(2)∵∠3=_______(已知)
∴a∥b(内错角相等,两直线平行)
(3)∵∠5+_______=180°(已知)
∴______∥_______(同旁内角互补,两直线平行)
8.(原创题)如图所示,写出所有角满足的条件使AB∥EF,并说明理由.
◆拓展创新
9.(应用题)(1)如图(1)所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.
判断AB与CD的位置关系,并说明理由;
(2)如图(2)所示在(1)的条件下,若小路OM平分∠EOB.通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N位置关系.
答案:
回顾归纳
1.同位角相等 2.内错角相等 3.同旁内角
课堂测控
1.∥ 2.b 3.∥ 4.∠2或∠3 5.∠EFD
6.∠ABC+∠BAD=180°或∠ADB=∠DBC或∠FAD=∠ABC.(任选一个即可).
解题规律:依照三个判定定理,同位角,内错角,同旁内角关系判定两直线平行.
课后测控
1.CD 2.∥ 3.D 4.C(点拨:①②④正确)
5.A(点拨:∠1=∠4得AB∥CD,∠1+∠2≠∠3+∠4,∠A+∠C≠180°)
6.已知,CD,同旁内角互补两直线平行,已知,∠3,等量代换
解题规律:EF∥GH成立→∠2+∠3=180°,又∠1=∠3,∴∠1+∠2=180°(已知)
7.(1)b (2)∠5 (3)∠4,a,b
思路点拨:由条件与结论关系及括号中定理判断填空内容.
8.①同位角∠A=∠CEF,∠B=∠EFC,
②内错角∠ADE=∠DEF,
③同旁内角.∠A+∠AEF=180°,∠B+∠BFE=180°,∠BDE+∠DEF=180°
思路点拨:AB,EF被AC所截,AB,EF被BC所截,AB,EF被DE所截,三个方面的关系中存在同位角,内错角,同旁内角来判定AB∥EF的条件.
9.(1)∵AB⊥EF,CD⊥EF
∴AB∥CD(两条直线都垂直于同一条直线,这两条直线平行)
(2)延长NO′至P,可证∠EOM=∠EO′P=45°,得OM∥O′N.
解题技巧:(1)中由垂线定义及平行线判定推理来证,
(2)中要作辅助线延长NO′至P,运用同位角相等来证明.
