人教版数学七年级下册 5.3 .1平行线的性质(一) 练习(word版含答案)
文档属性
| 名称 | 人教版数学七年级下册 5.3 .1平行线的性质(一) 练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 59.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 08:12:32 | ||
图片预览

文档简介
5.3 平行线的性质(一)
◆回顾归纳
1.两条平行直线被第三条直线所截,同位角_______,内错角____,同旁内角______.
2.同时垂直于两条平行线,并且夹在这两条平行线间的______叫做这两条平行线的距离.
◆课堂测控
知识点一 两直线平行 同位角相等
1.(2008,上海市)如图1所示,直线a∥b,且a,b被c所截,若∠1=40°,则∠2=______.
图1 图2 图3
知识点二 两直线平行 内错角相等
2.如图2所示,直线a∥b,且a,b被c所截,若∠1=60°,则∠2=_______,∠3=________.
知识点三 两直线平行 同旁内角互补
3.如图3所示,若AB∥CD,∠DEF=120°,则∠B=_______.
4.如图4所示,DE∥BC,DF∥AC,下列结论正确的个数为( )
①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFB
A.1个 B.2个 C.3个 D.4个
图4 图5
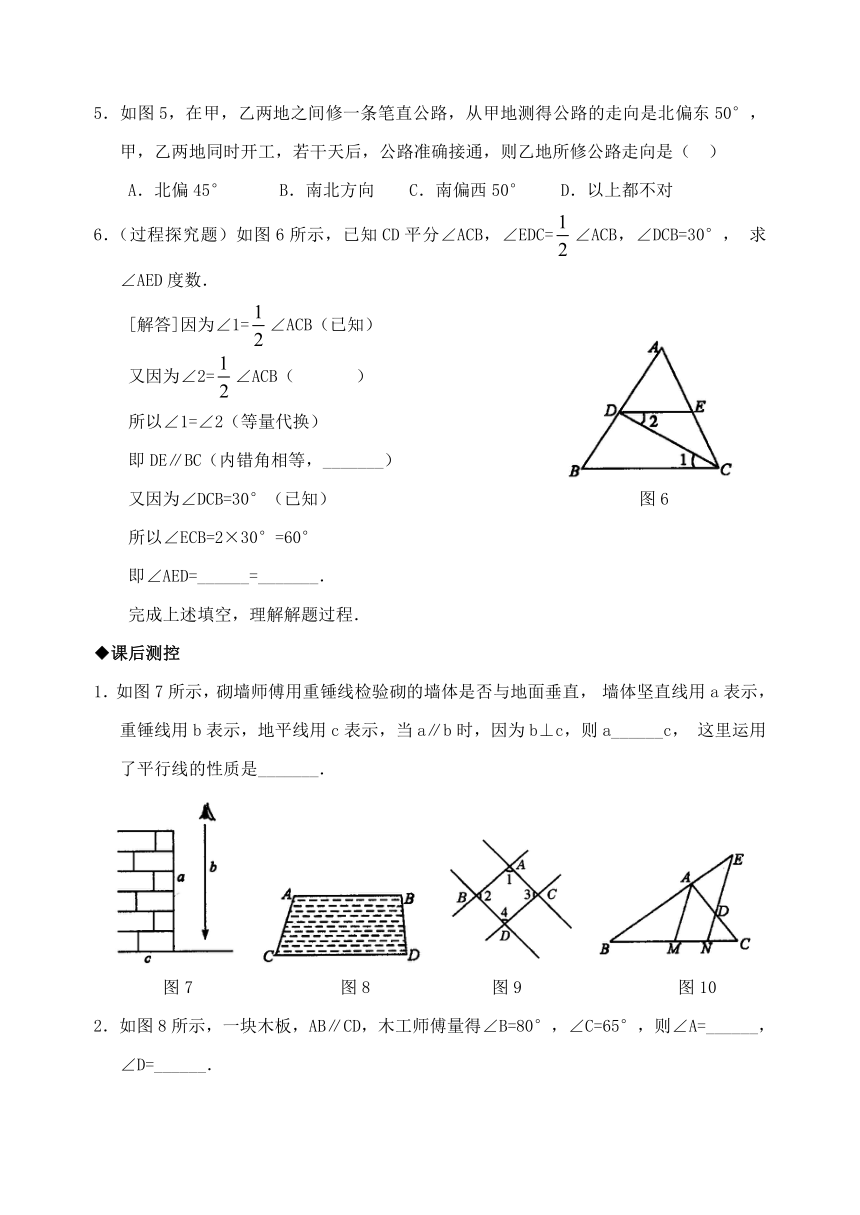
5.如图5,在甲,乙两地之间修一条笔直公路,从甲地测得公路的走向是北偏东50°,甲,乙两地同时开工,若干天后,公路准确接通,则乙地所修公路走向是( )
A.北偏45° B.南北方向 C.南偏西50° D.以上都不对
6.(过程探究题)如图6所示,已知CD平分∠ACB,∠EDC=∠ACB,∠DCB=30°,求∠AED度数.
[解答]因为∠1=∠ACB(已知)
又因为∠2=∠ACB( )
所以∠1=∠2(等量代换)
即DE∥BC(内错角相等,_______)
又因为∠DCB=30°(已知) 图6
所以∠ECB=2×30°=60°
即∠AED=______=_______.
完成上述填空,理解解题过程.
◆课后测控
1.如图7所示,砌墙师傅用重锤线检验砌的墙体是否与地面垂直,墙体坚直线用a表示,重锤线用b表示,地平线用c表示,当a∥b时,因为b⊥c,则a______c,这里运用了平行线的性质是_______.
图7 图8 图9 图10
2.如图8所示,一块木板,AB∥CD,木工师傅量得∠B=80°,∠C=65°,则∠A=______,∠D=______.
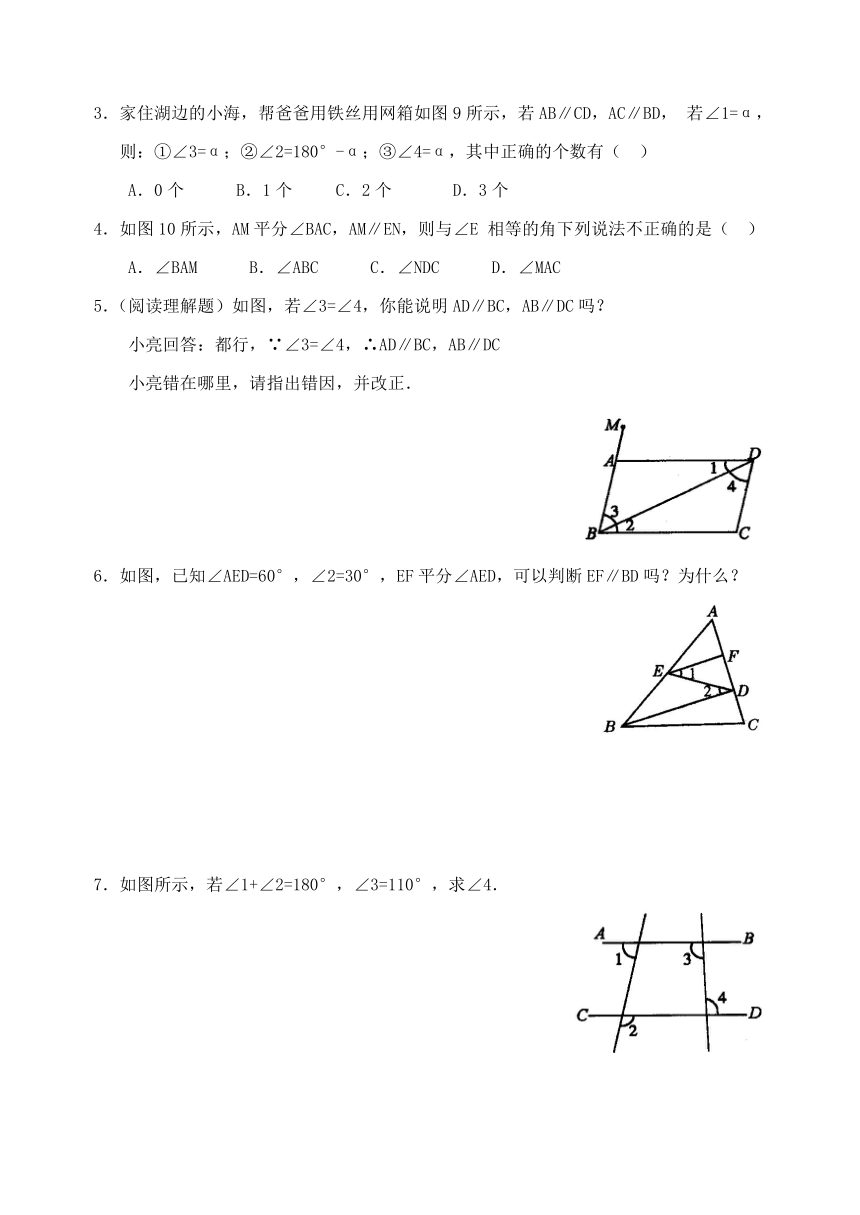
3.家住湖边的小海,帮爸爸用铁丝用网箱如图9所示,若AB∥CD,AC∥BD,若∠1=α,则:①∠3=α;②∠2=180°-α;③∠4=α,其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
4.如图10所示,AM平分∠BAC,AM∥EN,则与∠E相等的角下列说法不正确的是( )
A.∠BAM B.∠ABC C.∠NDC D.∠MAC
5.(阅读理解题)如图,若∠3=∠4,你能说明AD∥BC,AB∥DC吗?
小亮回答:都行,∵∠3=∠4,∴AD∥BC,AB∥DC
小亮错在哪里,请指出错因,并改正.
6.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
7.如图所示,若∠1+∠2=180°,∠3=110°,求∠4.
◆拓展创新
8.(探究题)如图所示,若AB∥CD,且∠1=∠2,试判断AM与CN位置关系,并说明理由.
答案:
回顾归纳
1.相等,相等,互补 2.线段的长度
课堂测控
1.40° 2.60°,120° 3.60°
4.D(点拨:∵DE∥BC,∴∠C=∠AED,∠EDF=∠BFD,∵DF∥AC,∴∠A=∠BDF,∵DE∥BC,DF∥AC,∴∠AED=∠DFB.)
5.C
6.已知,两直线平行,∠ECB,60°
解题规律:运用平行线性质及角平分线性质.
课后测控
1.⊥,两直线平行,同位角相等(同旁内角互补).
2.115°,100° 3.C(点拨:②④正确)
4.B(点拨:∠BAM=∠MAC=∠NDC.)
5.错误,不能识别AD∥BC.
因为∠3=∠4,所以AB∥CD.
思路点拨:∠3与∠4是直线AB,CD被BD所截得到的内错角.
6.可以,∵∠AED=60°,EF平分∠AED
∴∠FED=30°
又∵∠EDB=∠2=30°
∴EF∥BD
解题规律:证两直线平行,找内错角相等.
7.设∠2对顶角为∠5,则∠2=∠5
∵∠1+∠2=180°
∴∠1+∠5=180°
∴AB∥CD,∴∠3=∠4
又∵∠3=110°
∴∠4=110°
解题规律:先判断AB∥CD,再运用平行线的性质定理.
8.因为AB∥CD
所以∠EAB=∠ECD
又因为∠1=∠2
而∠EAM=∠EAB-∠1
∠ACN=∠ACD-∠2
即∠EAM=∠ACN
所以AM∥CN(同位角相等,两直线平行).
解题技巧:判断AM∥CN,①可证∠EAM=∠ECN,
②证∠MAC+∠ACN=180°,都能达到目的.
◆回顾归纳
1.两条平行直线被第三条直线所截,同位角_______,内错角____,同旁内角______.
2.同时垂直于两条平行线,并且夹在这两条平行线间的______叫做这两条平行线的距离.
◆课堂测控
知识点一 两直线平行 同位角相等
1.(2008,上海市)如图1所示,直线a∥b,且a,b被c所截,若∠1=40°,则∠2=______.
图1 图2 图3
知识点二 两直线平行 内错角相等
2.如图2所示,直线a∥b,且a,b被c所截,若∠1=60°,则∠2=_______,∠3=________.
知识点三 两直线平行 同旁内角互补
3.如图3所示,若AB∥CD,∠DEF=120°,则∠B=_______.
4.如图4所示,DE∥BC,DF∥AC,下列结论正确的个数为( )
①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFB
A.1个 B.2个 C.3个 D.4个
图4 图5
5.如图5,在甲,乙两地之间修一条笔直公路,从甲地测得公路的走向是北偏东50°,甲,乙两地同时开工,若干天后,公路准确接通,则乙地所修公路走向是( )
A.北偏45° B.南北方向 C.南偏西50° D.以上都不对
6.(过程探究题)如图6所示,已知CD平分∠ACB,∠EDC=∠ACB,∠DCB=30°,求∠AED度数.
[解答]因为∠1=∠ACB(已知)
又因为∠2=∠ACB( )
所以∠1=∠2(等量代换)
即DE∥BC(内错角相等,_______)
又因为∠DCB=30°(已知) 图6
所以∠ECB=2×30°=60°
即∠AED=______=_______.
完成上述填空,理解解题过程.
◆课后测控
1.如图7所示,砌墙师傅用重锤线检验砌的墙体是否与地面垂直,墙体坚直线用a表示,重锤线用b表示,地平线用c表示,当a∥b时,因为b⊥c,则a______c,这里运用了平行线的性质是_______.
图7 图8 图9 图10
2.如图8所示,一块木板,AB∥CD,木工师傅量得∠B=80°,∠C=65°,则∠A=______,∠D=______.
3.家住湖边的小海,帮爸爸用铁丝用网箱如图9所示,若AB∥CD,AC∥BD,若∠1=α,则:①∠3=α;②∠2=180°-α;③∠4=α,其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
4.如图10所示,AM平分∠BAC,AM∥EN,则与∠E相等的角下列说法不正确的是( )
A.∠BAM B.∠ABC C.∠NDC D.∠MAC
5.(阅读理解题)如图,若∠3=∠4,你能说明AD∥BC,AB∥DC吗?
小亮回答:都行,∵∠3=∠4,∴AD∥BC,AB∥DC
小亮错在哪里,请指出错因,并改正.
6.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
7.如图所示,若∠1+∠2=180°,∠3=110°,求∠4.
◆拓展创新
8.(探究题)如图所示,若AB∥CD,且∠1=∠2,试判断AM与CN位置关系,并说明理由.
答案:
回顾归纳
1.相等,相等,互补 2.线段的长度
课堂测控
1.40° 2.60°,120° 3.60°
4.D(点拨:∵DE∥BC,∴∠C=∠AED,∠EDF=∠BFD,∵DF∥AC,∴∠A=∠BDF,∵DE∥BC,DF∥AC,∴∠AED=∠DFB.)
5.C
6.已知,两直线平行,∠ECB,60°
解题规律:运用平行线性质及角平分线性质.
课后测控
1.⊥,两直线平行,同位角相等(同旁内角互补).
2.115°,100° 3.C(点拨:②④正确)
4.B(点拨:∠BAM=∠MAC=∠NDC.)
5.错误,不能识别AD∥BC.
因为∠3=∠4,所以AB∥CD.
思路点拨:∠3与∠4是直线AB,CD被BD所截得到的内错角.
6.可以,∵∠AED=60°,EF平分∠AED
∴∠FED=30°
又∵∠EDB=∠2=30°
∴EF∥BD
解题规律:证两直线平行,找内错角相等.
7.设∠2对顶角为∠5,则∠2=∠5
∵∠1+∠2=180°
∴∠1+∠5=180°
∴AB∥CD,∴∠3=∠4
又∵∠3=110°
∴∠4=110°
解题规律:先判断AB∥CD,再运用平行线的性质定理.
8.因为AB∥CD
所以∠EAB=∠ECD
又因为∠1=∠2
而∠EAM=∠EAB-∠1
∠ACN=∠ACD-∠2
即∠EAM=∠ACN
所以AM∥CN(同位角相等,两直线平行).
解题技巧:判断AM∥CN,①可证∠EAM=∠ECN,
②证∠MAC+∠ACN=180°,都能达到目的.
