4.2.5正态分布人教B版(2019)选择性必修二(共24张PPT)
文档属性
| 名称 | 4.2.5正态分布人教B版(2019)选择性必修二(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 21:34:29 | ||
图片预览






文档简介
(共24张PPT)
4.2.5正态分布
学习目标
(1)通过误差模型,了解服从正态分布的随机变量
(2)通过具体实例,借助频率直方图的几何直观,了解正态分布的特征
(3)了解正态分布的均值、方差及其含义
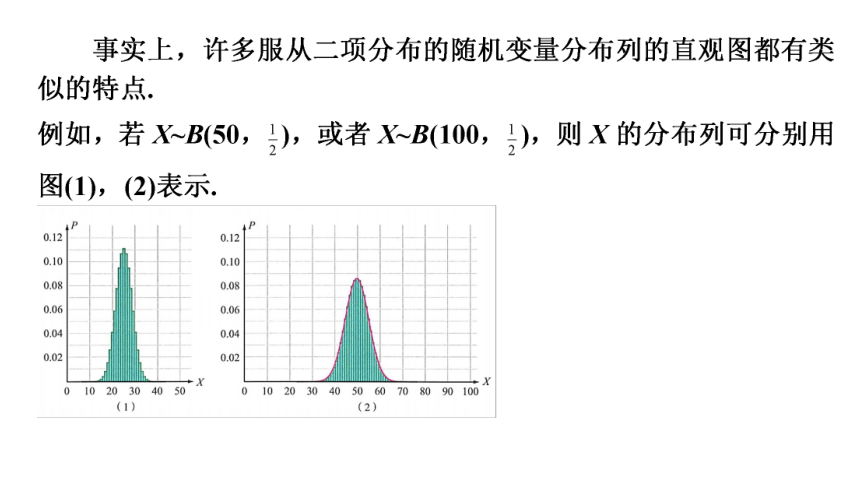
已知X服从参数为100,0.5的二项分布,即X~B(100,0.5),你能手工计算出P(X=50)的值吗?
尝试与发现
回想:二项分布的概率公式
有没有其他办法能得到上式的近似值呢?
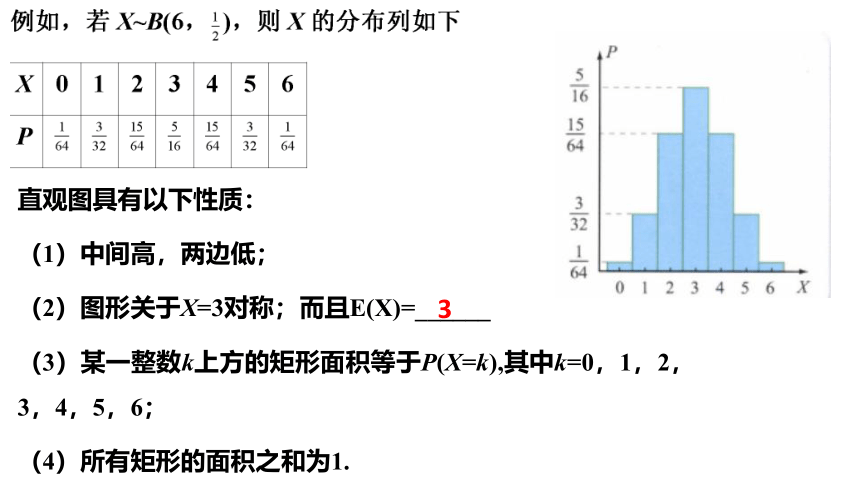
直观图具有以下性质:
(1)中间高,两边低;
(2)图形关于X=3对称;而且E(X)=______
(3)某一整数k上方的矩形面积等于P(X=k),其中k=0,1,2,3,4,5,6;
(4)所有矩形的面积之和为1.
3
正态曲线
一般地,φ(x)对应的图像称为正态曲线
正态曲线的性质
(1)正态曲线关于x=μ对称(即μ决定正态曲线对称轴的位置),
具有中间高、两边低的特点;
(2)正态曲线与x轴所围成的图形面积为1;
(3)σ决定正态曲线的“胖瘦”:σ越大,说明标准差越大,数据的集中程度越弱,
所以曲线越“胖”;σ越小,说明标准差越小,数据的集中程度越强,所以曲线越“瘦”.
φ(x)的最大值是多少?
简记为“大胖小瘦”
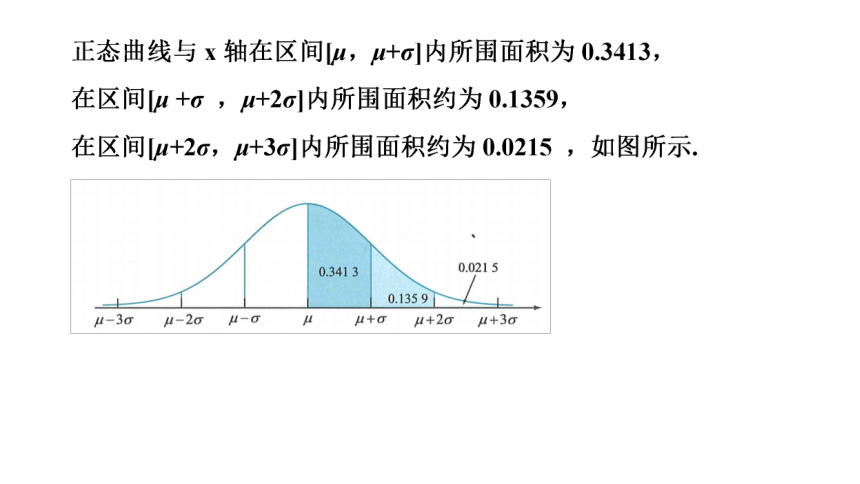
例1.求正态曲线与x轴在下列区间内所围面积(精确到0.001)
(1)[μ,+∞); (2)[μ -σ ,μ+σ]
(3)[μ-2σ,μ+2σ] (4)[μ-3σ,μ+3σ].
应用举例
注意:面积的大小与区间的开闭无关
概念解析
μ是X的平均值, σ是X的标准差,σ2是X的方差
正态分布
当取值几乎总
取值于区间-3,3
区间取值几乎不可能在实际应用中就只考虑这个区间,称为原则
现实生活中,很多随机变量都服从或近似服从正态分布:
在生产中,正常条件下生产出来的产品尺寸
在测量中,随机误差
在生物学中,同一地区同龄人的身高、同一批灯泡的寿命
在考试中,考试成绩
例2. 假设某地区高二学生的身高服从正态分布,且均值为170(单位:cm,下同),标准差为10.在该地区任意抽取一名高二学生,求这名学生的身高:
(1)不高于170的概率;
(2)在区间[160,180]内的概率;
(3)不高于180的概率.
应用举例
(2)正态曲线关于直线对称,从而在关于对称的区间上概率相等
服从正态分布的随机变量在某个区间内取值概率的方法
(1)充分利用正态曲线的对称性及面积为1的性质求解
(3)P(Xμ+a)
方法归纳
应用举例
转化的思想
概念解析
标准正态分布
以下是a ≥ 0时部分Φ(a)的值:
应用举例
解:(1)P(X < 0.28)= Φ(a)= 0.6103;
(2)P(X < -0.36)=Φ(-0.36)=1-Φ(0.36)=0.3594
(3)P(0.18≤X < 0.57)= P(X < 0.57) -P(X <0.18 )
= Φ(0.57) -Φ(0.18) =0.1443.
课堂小结
(1)二项分布与正态曲线,曲线的性质与特点
(2)正态分布与3σ原则
(3)标准正态分布
4.2.5正态分布
学习目标
(1)通过误差模型,了解服从正态分布的随机变量
(2)通过具体实例,借助频率直方图的几何直观,了解正态分布的特征
(3)了解正态分布的均值、方差及其含义
已知X服从参数为100,0.5的二项分布,即X~B(100,0.5),你能手工计算出P(X=50)的值吗?
尝试与发现
回想:二项分布的概率公式
有没有其他办法能得到上式的近似值呢?
直观图具有以下性质:
(1)中间高,两边低;
(2)图形关于X=3对称;而且E(X)=______
(3)某一整数k上方的矩形面积等于P(X=k),其中k=0,1,2,3,4,5,6;
(4)所有矩形的面积之和为1.
3
正态曲线
一般地,φ(x)对应的图像称为正态曲线
正态曲线的性质
(1)正态曲线关于x=μ对称(即μ决定正态曲线对称轴的位置),
具有中间高、两边低的特点;
(2)正态曲线与x轴所围成的图形面积为1;
(3)σ决定正态曲线的“胖瘦”:σ越大,说明标准差越大,数据的集中程度越弱,
所以曲线越“胖”;σ越小,说明标准差越小,数据的集中程度越强,所以曲线越“瘦”.
φ(x)的最大值是多少?
简记为“大胖小瘦”
例1.求正态曲线与x轴在下列区间内所围面积(精确到0.001)
(1)[μ,+∞); (2)[μ -σ ,μ+σ]
(3)[μ-2σ,μ+2σ] (4)[μ-3σ,μ+3σ].
应用举例
注意:面积的大小与区间的开闭无关
概念解析
μ是X的平均值, σ是X的标准差,σ2是X的方差
正态分布
当取值几乎总
取值于区间-3,3
区间取值几乎不可能在实际应用中就只考虑这个区间,称为原则
现实生活中,很多随机变量都服从或近似服从正态分布:
在生产中,正常条件下生产出来的产品尺寸
在测量中,随机误差
在生物学中,同一地区同龄人的身高、同一批灯泡的寿命
在考试中,考试成绩
例2. 假设某地区高二学生的身高服从正态分布,且均值为170(单位:cm,下同),标准差为10.在该地区任意抽取一名高二学生,求这名学生的身高:
(1)不高于170的概率;
(2)在区间[160,180]内的概率;
(3)不高于180的概率.
应用举例
(2)正态曲线关于直线对称,从而在关于对称的区间上概率相等
服从正态分布的随机变量在某个区间内取值概率的方法
(1)充分利用正态曲线的对称性及面积为1的性质求解
(3)P(X
方法归纳
应用举例
转化的思想
概念解析
标准正态分布
以下是a ≥ 0时部分Φ(a)的值:
应用举例
解:(1)P(X < 0.28)= Φ(a)= 0.6103;
(2)P(X < -0.36)=Φ(-0.36)=1-Φ(0.36)=0.3594
(3)P(0.18≤X < 0.57)= P(X < 0.57) -P(X <0.18 )
= Φ(0.57) -Φ(0.18) =0.1443.
课堂小结
(1)二项分布与正态曲线,曲线的性质与特点
(2)正态分布与3σ原则
(3)标准正态分布
