八年级数学下册17.1 勾股定理 随堂练习(word版含答案)
文档属性
| 名称 | 八年级数学下册17.1 勾股定理 随堂练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 170.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 08:19:10 | ||
图片预览

文档简介
17.1《勾股定理》随堂练习
2021-2022学年人教版八年级数学下册
一、单选题
1.若直角三角形的一条直角边长为9,斜边长为10,则另一条直角边长为( ).
A.1 B. C.19 D.3
2.在中,,若,,则的长为( )
A. B.5 C.6 D.7
3.已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
4.已知RtABC中,∠C=90°,若a+b=14cm,c=10cm,则RtABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
5.直角三角形中一直角边的长为18,另两边长为连续偶数,则直角三角形的周长为( ).
A.242 B.240 C.180 D.不能确定
6.在中,,,则( ).
A.100 B.200 C.300 D.400
7.在中,,的三边是a、b、c,则以下结论正确的是( ).
A. B. C. D.以上答案都不对
8.在中,两直角边都扩大2倍,则斜边扩大为原来的( ).
A.2倍 B.3倍 C.4倍 D.倍
二、填空题
9.在中,,(1)若,,则________.(2)若,,则________.
10.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得米,,则江面的宽度为________.
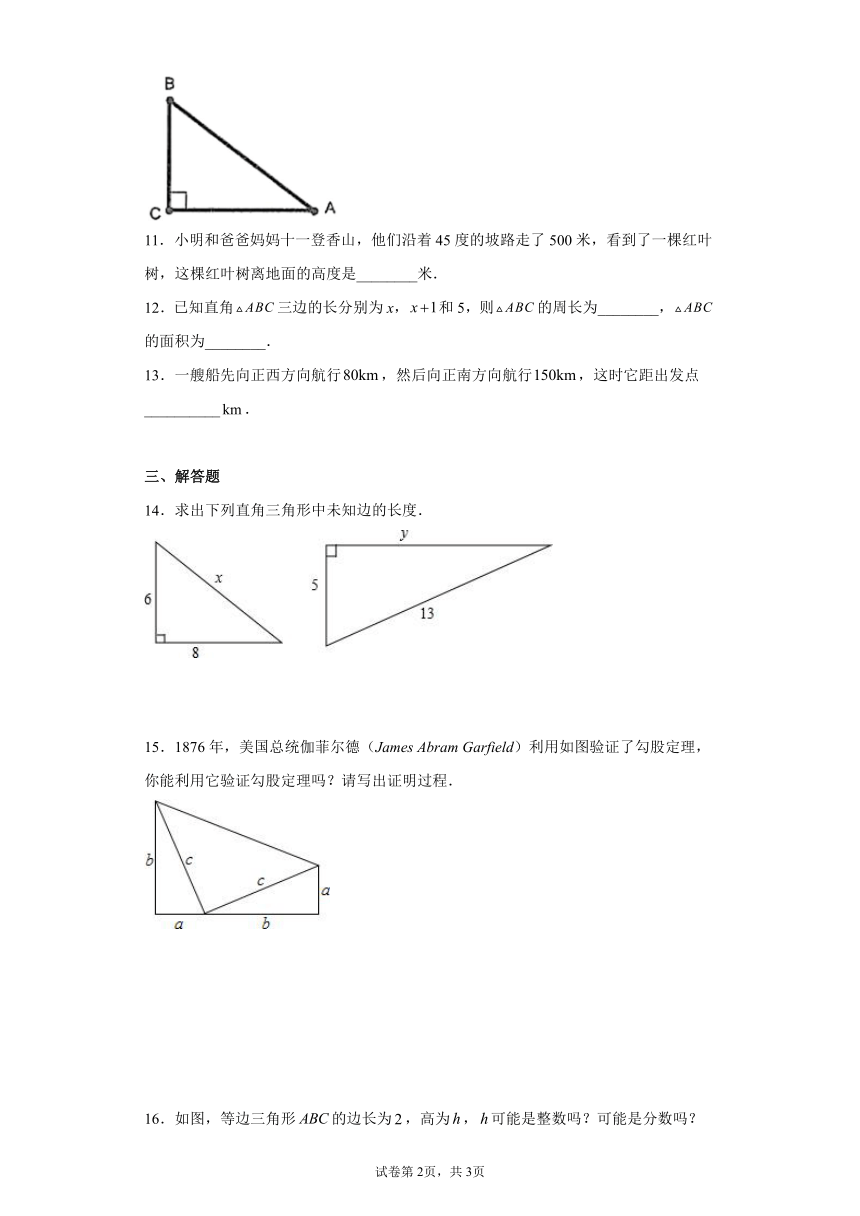
11.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树离地面的高度是________米.
12.已知直角三边的长分别为x,和5,则的周长为________,的面积为________.
13.一艘船先向正西方向航行,然后向正南方向航行,这时它距出发点__________.
三、解答题
14.求出下列直角三角形中未知边的长度.
15.1876年,美国总统伽菲尔德(James Abram Garfield)利用如图验证了勾股定理,你能利用它验证勾股定理吗?请写出证明过程.
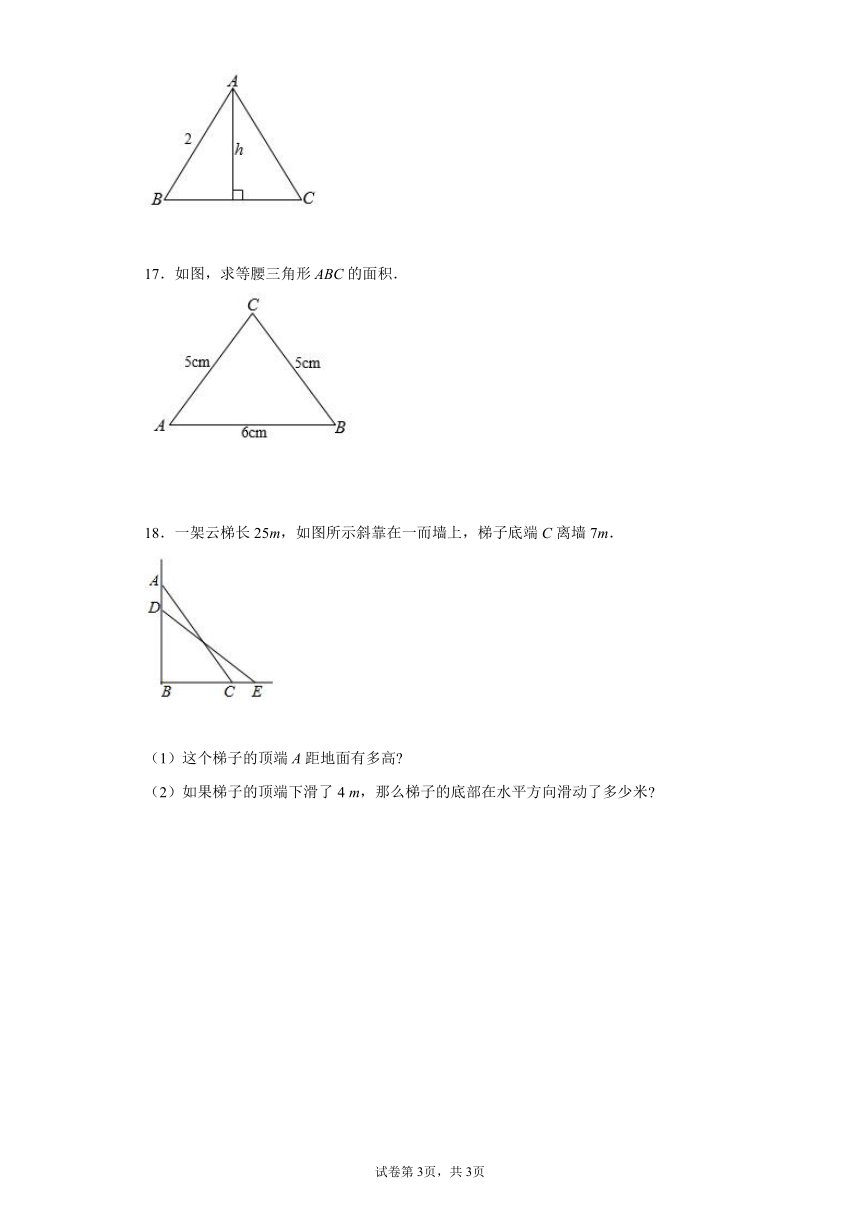
16.如图,等边三角形的边长为,高为,可能是整数吗?可能是分数吗?
17.如图,求等腰三角形ABC的面积.
18.一架云梯长25m,如图所示斜靠在一而墙上,梯子底端C离墙7m.
(1)这个梯子的顶端A距地面有多高
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向滑动了多少米
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
2.B
3.D
4.A
5.C
6.C
7.A
8.A
9.(1)17; (2)
10.米
11.
12.12或30 6或30
13.170
14.
解:图1中:x=;
图2中:y=.
15.
解:能,理由如下:
∵直角梯形的面积等于三个直角三角形的面积之和,
∴ (a+b)(a+b)=2×ab+c2,
∴(a+b)(a+b)=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
16.
解:∵等边三角形三线合一
∴D为BC的中点,且AD⊥BC,
即BD=CD=1,
∵AB=2,
∴AD=,
即=
故不可能是整数,也不可能是分数.
17.
解:过点C作CD⊥AB于点D,
∵AC=BC,DC⊥AB,
∴AD=BD=AB=3cm,
∵BC=5cm,
∴DC==4(cm),
∴等腰三角形ABC的面积为:×4×6=12(cm2).
18.
解:(1)由题意可知:,;,
在中,由勾股定理得:
,
∴
,
因此,这个梯子的顶端距地面有高.
(2)由图可知:AD=4m,
,
在中,由勾股定理得:
,
∴
,
∴.
答:梯子的底部在水平方向滑动了.
答案第1页,共2页
答案第1页,共2页
2021-2022学年人教版八年级数学下册
一、单选题
1.若直角三角形的一条直角边长为9,斜边长为10,则另一条直角边长为( ).
A.1 B. C.19 D.3
2.在中,,若,,则的长为( )
A. B.5 C.6 D.7
3.已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
4.已知RtABC中,∠C=90°,若a+b=14cm,c=10cm,则RtABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
5.直角三角形中一直角边的长为18,另两边长为连续偶数,则直角三角形的周长为( ).
A.242 B.240 C.180 D.不能确定
6.在中,,,则( ).
A.100 B.200 C.300 D.400
7.在中,,的三边是a、b、c,则以下结论正确的是( ).
A. B. C. D.以上答案都不对
8.在中,两直角边都扩大2倍,则斜边扩大为原来的( ).
A.2倍 B.3倍 C.4倍 D.倍
二、填空题
9.在中,,(1)若,,则________.(2)若,,则________.
10.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得米,,则江面的宽度为________.
11.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树离地面的高度是________米.
12.已知直角三边的长分别为x,和5,则的周长为________,的面积为________.
13.一艘船先向正西方向航行,然后向正南方向航行,这时它距出发点__________.
三、解答题
14.求出下列直角三角形中未知边的长度.
15.1876年,美国总统伽菲尔德(James Abram Garfield)利用如图验证了勾股定理,你能利用它验证勾股定理吗?请写出证明过程.
16.如图,等边三角形的边长为,高为,可能是整数吗?可能是分数吗?
17.如图,求等腰三角形ABC的面积.
18.一架云梯长25m,如图所示斜靠在一而墙上,梯子底端C离墙7m.
(1)这个梯子的顶端A距地面有多高
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向滑动了多少米
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
2.B
3.D
4.A
5.C
6.C
7.A
8.A
9.(1)17; (2)
10.米
11.
12.12或30 6或30
13.170
14.
解:图1中:x=;
图2中:y=.
15.
解:能,理由如下:
∵直角梯形的面积等于三个直角三角形的面积之和,
∴ (a+b)(a+b)=2×ab+c2,
∴(a+b)(a+b)=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
16.
解:∵等边三角形三线合一
∴D为BC的中点,且AD⊥BC,
即BD=CD=1,
∵AB=2,
∴AD=,
即=
故不可能是整数,也不可能是分数.
17.
解:过点C作CD⊥AB于点D,
∵AC=BC,DC⊥AB,
∴AD=BD=AB=3cm,
∵BC=5cm,
∴DC==4(cm),
∴等腰三角形ABC的面积为:×4×6=12(cm2).
18.
解:(1)由题意可知:,;,
在中,由勾股定理得:
,
∴
,
因此,这个梯子的顶端距地面有高.
(2)由图可知:AD=4m,
,
在中,由勾股定理得:
,
∴
,
∴.
答:梯子的底部在水平方向滑动了.
答案第1页,共2页
答案第1页,共2页
