河南省漯河市郾城高级中学2012-2013学年高一上学期期中考试数学(文)试题
文档属性
| 名称 | 河南省漯河市郾城高级中学2012-2013学年高一上学期期中考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 193.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-23 19:30:34 | ||
图片预览




文档简介
2012-2013学年度(上)高一期中考试
数学(文)试题
一、 选择题 (本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,定义域为的是 ( )
(A) (B) (C) (D)
2.已知集合的所有元素之和为( )
(A) (B) (C) (D)
3.下列各组函数为同一函数的是 ( )
(A), (B)
(C) (D)
4.函数的奇偶性为 ( )
(A)奇函数 (B)偶函数
(C)非奇非偶函数 (D)既奇又偶函数
5.已知函数的图象与直线的公共点个数为( )
(A)恰有一个 (B)至少有一个 (C)至多一个 (D)0
6.函数的图象的大致形状是 ( )
7.设函数,若,则实数= ( )
(A)-4或-2 (B)-4或2 (C)-2或4 (D)-2或2
8.函数的零点一定在下列哪个区间( )
(A)(1,2) ( B)(2,3) (C)(3,4) ( D)(5,6)
9.用一平面去截体积为的球,所得截面的面积为,则球心到截面的距离为( )
(A) 8 (B) 9 (C) (D) 3
10.若集合,则实数的值的集合是( )
(A) (B)
(C) (D)
11.设奇函数在上为增函数,且,则不等式的解集为 )
(A) (B)
(C) (D)
12. 定义,设集合则集合的所有元素之和为( )
(A)3 (B)9 (C)18 (D)27
二、填空题 (本大题共4小题,每小题5分,满分20分)
函数 ,则 ;
若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于_____________
15、已知函数,若,则_________.
16.集合,若只有一个子集,则实数的取值范围是 .
三.解答题:(本大题共6小题,其中第17题10分,第18、19、20、21、22各12分)
17.(本题满分10分)
化简下列式子
(1)
(2)
18.(本题满分12分)
设集合,, 。
(1)求;
(2)若,求实数的取值范围.
19.(本小题满分12分)
已知函数,且,
(1)求、的值;
(2)判断函数的奇偶性.
20.(本小题满分12分)
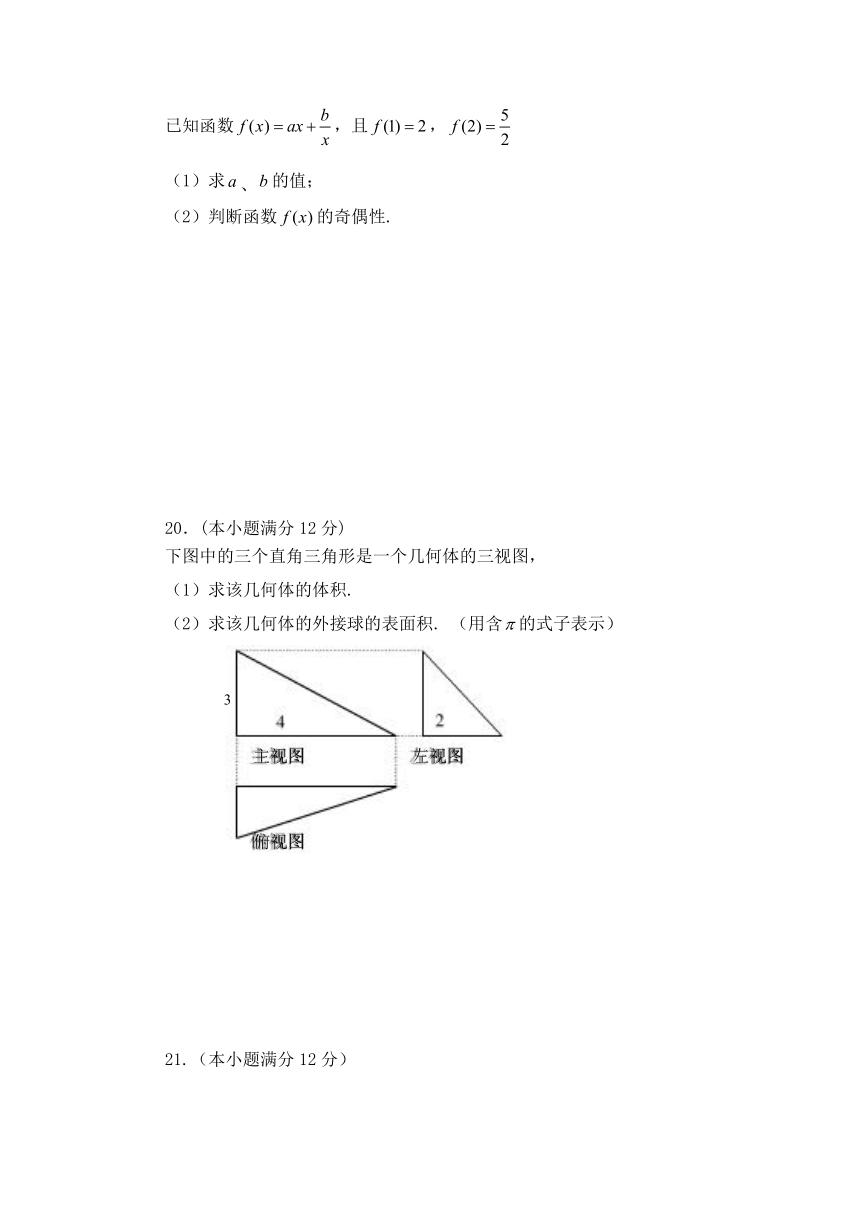
下图中的三个直角三角形是一个几何体的三视图,
(1)求该几何体的体积.
(2)求该几何体的外接球的表面积. (用含的式子表示)
21.(本小题满分12分)
已知函数,(其中为常数且)的图象经过点
(1)求的解析式
(2)若不等式在上恒成立,求实数的取值范围
22.(本小题满分12分)
已知二次函数
若,且.
求的解析式,并求在区间上的最大值与最小值。
(2)若在上具有单调性,求实数的范围
高一数学(文科)参考答案
一、 选择题 (本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1-6 A,B,B,C,C,C 7-12 ,B,B,C,D,D,C
提示:
A中x>0 B中 C中 D中
中,由得或由得x=1,由得x=-3或x=1,所以A={1,-3},所以所有元素之和为-2
A中: B中: C中:对于,,对于,
D中:都有,但解析式不同 即对应关系不同
由且得且所以所以定义域中只有一个元素1,所以非奇非偶
是函数,而是与x轴垂直的直线,所以与的图像可能有交点也可能没有交点. 根据函数的定义知,若有交点,也只能有一个交点,所以交点的个数至多有一个.
=当x>0时函数是增函数,当x<0时函数是减函数 ,故C
当时,-a=4,a=-4,当a>0时,a=2,所以选B
对于A:
对于B:所以选B
设球的半径为R,截面圆的半径为r,则则因为球心与截面圆心的连线垂直截面圆,球半径R、截面圆半径r和球心到截面的距离d构成直角三角形,由勾股定理得d=
当a=0时,A=合题意;当a0时,因为题中不等式是小于号“<”只有a>0图象开口向上且即时才有A=,综上两种情况知实数的值的集合是{a|},故选D
因为是奇函数又
所以;当x<0时f(x)>0,当x>0时f(x)<0,又奇函数在上为增函数,且画出图像草图知选D
把当作公式用。当x=0时y=1或2,z=0;当x=2时y=1或2,z=xy+x÷y=2×1+2÷1=4或z=2×2+2÷2=5,设M=则M={0,4,5},则=MC,把公式再用一次,就可求出,即x=0,4或5时y=1,z=0,4×1+4÷1或5×1+5÷1,z=0,8或10,所以
=MC={0,8,10},所有元素之和为18
填空题 (本大题共4小题,每小题5分,满分20分)
; 14、 15、 16、
提示:
=-2×(-2)=4,
由底面是正三角形的三棱柱的正视图知,几何体是正三棱柱,且底面的边长为2,高为1
表面积=2×底面积+侧面积=2×三角形面积+三角形的周长×高
=
∵.∴又∴
∴
16.∵若只有一个子集,则=,由图象知实数的取值范围是(当即01时结果一样)
三.解答题:(本大题共6小题,其中17题10分;18、19、20,21、22每题12分)
17题:(本题满分10分)
………………5分
………………10分
18题:(本题满分12分)
解:(1)
∵
∴ …………………6分
(2)∵,∴
∴,∴
∴实数a的范围是 ……………………………12分
19题:(本题满分12分)(1)依题意有 ,
得 ………………6分
(2)的定义域为关于原点对称, …9分
∵ ∴函数为奇函数。 ……12分
(本题满分12分)
(1)解:由三视图可知该几何体为三棱锥,此三棱锥的底面为直角三角形,直角边长分别为2,4,且过底面的直角顶点的侧棱和底面垂直,该棱长为3,即棱锥的高为3,棱锥的体积为V= ……6分
(2)把三棱锥补成长方体,则长方体的对角线长等于其外接球的直径,设球的半径为R,∵长方体的对角线长,∴2R=,R=
∴外接球的表面积S== ……………12分
21.(本小题满分12分)
(1)由题意得……………6分
(2)设,则在上为减函数
(可以不证明)当时
在上恒成立,即在上恒成立,
∴
的取值范围为: ………………………12分
22题 (本小题满分12分)
解:(1)∵,∴, …………1分
∴
∴………2分
∴
∴ …………………4分
∵,∴在上是减函数,在上是增函数
又>
∴。 ……………6分
(2),从而该函数的对称轴方程为……7分
当函数在上为单调递增时,则,从而……………9分
当函数在上为单调递减时,则,从而……………11分
综上得:的取值范围是………12分
数学(文)试题
一、 选择题 (本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,定义域为的是 ( )
(A) (B) (C) (D)
2.已知集合的所有元素之和为( )
(A) (B) (C) (D)
3.下列各组函数为同一函数的是 ( )
(A), (B)
(C) (D)
4.函数的奇偶性为 ( )
(A)奇函数 (B)偶函数
(C)非奇非偶函数 (D)既奇又偶函数
5.已知函数的图象与直线的公共点个数为( )
(A)恰有一个 (B)至少有一个 (C)至多一个 (D)0
6.函数的图象的大致形状是 ( )
7.设函数,若,则实数= ( )
(A)-4或-2 (B)-4或2 (C)-2或4 (D)-2或2
8.函数的零点一定在下列哪个区间( )
(A)(1,2) ( B)(2,3) (C)(3,4) ( D)(5,6)
9.用一平面去截体积为的球,所得截面的面积为,则球心到截面的距离为( )
(A) 8 (B) 9 (C) (D) 3
10.若集合,则实数的值的集合是( )
(A) (B)
(C) (D)
11.设奇函数在上为增函数,且,则不等式的解集为 )
(A) (B)
(C) (D)
12. 定义,设集合则集合的所有元素之和为( )
(A)3 (B)9 (C)18 (D)27
二、填空题 (本大题共4小题,每小题5分,满分20分)
函数 ,则 ;
若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于_____________
15、已知函数,若,则_________.
16.集合,若只有一个子集,则实数的取值范围是 .
三.解答题:(本大题共6小题,其中第17题10分,第18、19、20、21、22各12分)
17.(本题满分10分)
化简下列式子
(1)
(2)
18.(本题满分12分)
设集合,, 。
(1)求;
(2)若,求实数的取值范围.
19.(本小题满分12分)
已知函数,且,
(1)求、的值;
(2)判断函数的奇偶性.
20.(本小题满分12分)
下图中的三个直角三角形是一个几何体的三视图,
(1)求该几何体的体积.
(2)求该几何体的外接球的表面积. (用含的式子表示)
21.(本小题满分12分)
已知函数,(其中为常数且)的图象经过点
(1)求的解析式
(2)若不等式在上恒成立,求实数的取值范围
22.(本小题满分12分)
已知二次函数
若,且.
求的解析式,并求在区间上的最大值与最小值。
(2)若在上具有单调性,求实数的范围
高一数学(文科)参考答案
一、 选择题 (本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1-6 A,B,B,C,C,C 7-12 ,B,B,C,D,D,C
提示:
A中x>0 B中 C中 D中
中,由得或由得x=1,由得x=-3或x=1,所以A={1,-3},所以所有元素之和为-2
A中: B中: C中:对于,,对于,
D中:都有,但解析式不同 即对应关系不同
由且得且所以所以定义域中只有一个元素1,所以非奇非偶
是函数,而是与x轴垂直的直线,所以与的图像可能有交点也可能没有交点. 根据函数的定义知,若有交点,也只能有一个交点,所以交点的个数至多有一个.
=当x>0时函数是增函数,当x<0时函数是减函数 ,故C
当时,-a=4,a=-4,当a>0时,a=2,所以选B
对于A:
对于B:所以选B
设球的半径为R,截面圆的半径为r,则则因为球心与截面圆心的连线垂直截面圆,球半径R、截面圆半径r和球心到截面的距离d构成直角三角形,由勾股定理得d=
当a=0时,A=合题意;当a0时,因为题中不等式是小于号“<”只有a>0图象开口向上且即时才有A=,综上两种情况知实数的值的集合是{a|},故选D
因为是奇函数又
所以;当x<0时f(x)>0,当x>0时f(x)<0,又奇函数在上为增函数,且画出图像草图知选D
把当作公式用。当x=0时y=1或2,z=0;当x=2时y=1或2,z=xy+x÷y=2×1+2÷1=4或z=2×2+2÷2=5,设M=则M={0,4,5},则=MC,把公式再用一次,就可求出,即x=0,4或5时y=1,z=0,4×1+4÷1或5×1+5÷1,z=0,8或10,所以
=MC={0,8,10},所有元素之和为18
填空题 (本大题共4小题,每小题5分,满分20分)
; 14、 15、 16、
提示:
=-2×(-2)=4,
由底面是正三角形的三棱柱的正视图知,几何体是正三棱柱,且底面的边长为2,高为1
表面积=2×底面积+侧面积=2×三角形面积+三角形的周长×高
=
∵.∴又∴
∴
16.∵若只有一个子集,则=,由图象知实数的取值范围是(当即0
三.解答题:(本大题共6小题,其中17题10分;18、19、20,21、22每题12分)
17题:(本题满分10分)
………………5分
………………10分
18题:(本题满分12分)
解:(1)
∵
∴ …………………6分
(2)∵,∴
∴,∴
∴实数a的范围是 ……………………………12分
19题:(本题满分12分)(1)依题意有 ,
得 ………………6分
(2)的定义域为关于原点对称, …9分
∵ ∴函数为奇函数。 ……12分
(本题满分12分)
(1)解:由三视图可知该几何体为三棱锥,此三棱锥的底面为直角三角形,直角边长分别为2,4,且过底面的直角顶点的侧棱和底面垂直,该棱长为3,即棱锥的高为3,棱锥的体积为V= ……6分
(2)把三棱锥补成长方体,则长方体的对角线长等于其外接球的直径,设球的半径为R,∵长方体的对角线长,∴2R=,R=
∴外接球的表面积S== ……………12分
21.(本小题满分12分)
(1)由题意得……………6分
(2)设,则在上为减函数
(可以不证明)当时
在上恒成立,即在上恒成立,
∴
的取值范围为: ………………………12分
22题 (本小题满分12分)
解:(1)∵,∴, …………1分
∴
∴………2分
∴
∴ …………………4分
∵,∴在上是减函数,在上是增函数
又>
∴。 ……………6分
(2),从而该函数的对称轴方程为……7分
当函数在上为单调递增时,则,从而……………9分
当函数在上为单调递减时,则,从而……………11分
综上得:的取值范围是………12分
同课章节目录
