2021-2022学年人教版数学八年级下册18.1.1平行四边形的性质 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.1.1平行四边形的性质 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
18.1.1平行四边形的性质2
人教版八年级下册
第18章平行四边形
01
理掌握平行四边形对角线互相平分的性质。
02
能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题。
教学目标
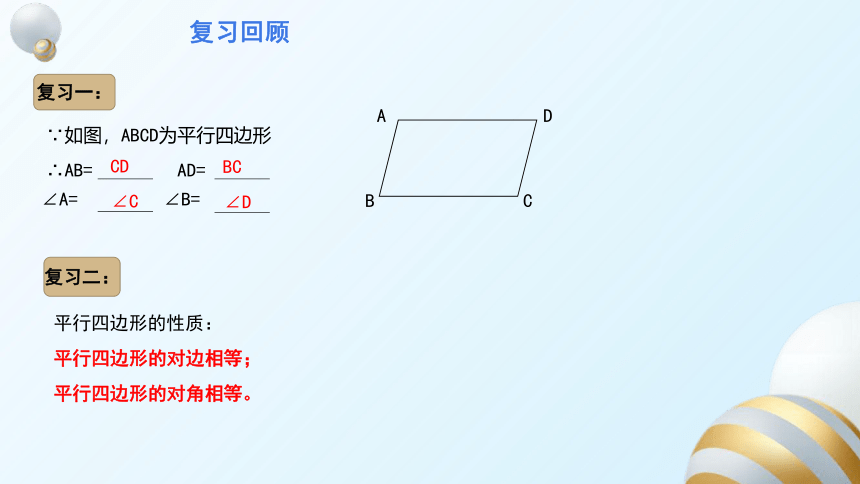
复习回顾
B
A
C
D
∵如图,ABCD为平行四边形
∴AB= AD=
复习一:
∠A= ∠B=
CD
BC
∠C
∠D
复习二:
平行四边形的性质:
平行四边形的对边相等;
平行四边形的对角相等。
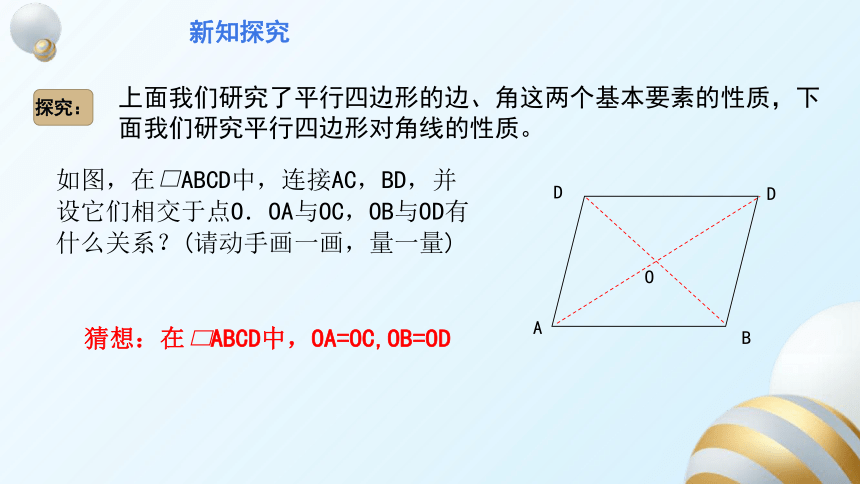
新知探究
探究:
上面我们研究了平行四边形的边、角这两个基本要素的性质,下面我们研究平行四边形对角线的性质。
如图,在 ABCD中,连接AC,BD,并设它们相交于点O.OA与OC,OB与OD有什么关系?(请动手画一画,量一量)
D
A
B
D
O
猜想:在 ABCD中,OA=OC,OB=OD
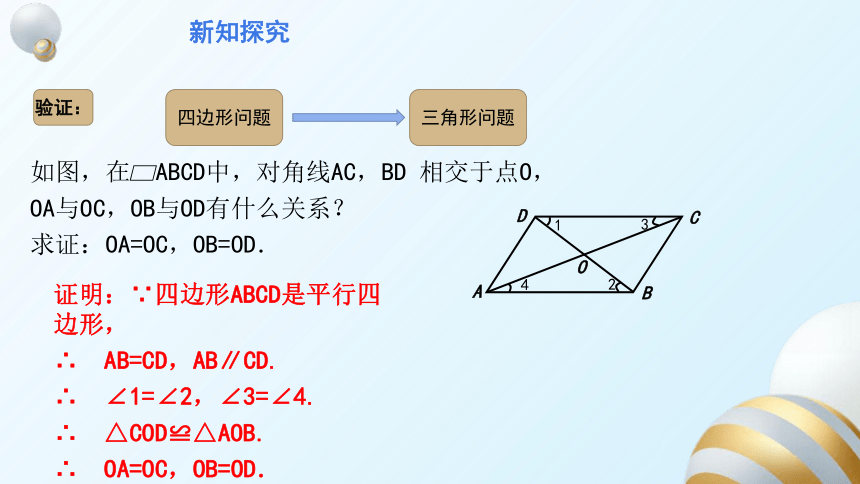
新知探究
验证:
四边形问题
三角形问题
如图,在 ABCD中,对角线AC,BD 相交于点O,
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
证明:∵四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ △COD≌△AOB.
∴ OA=OC,OB=OD.
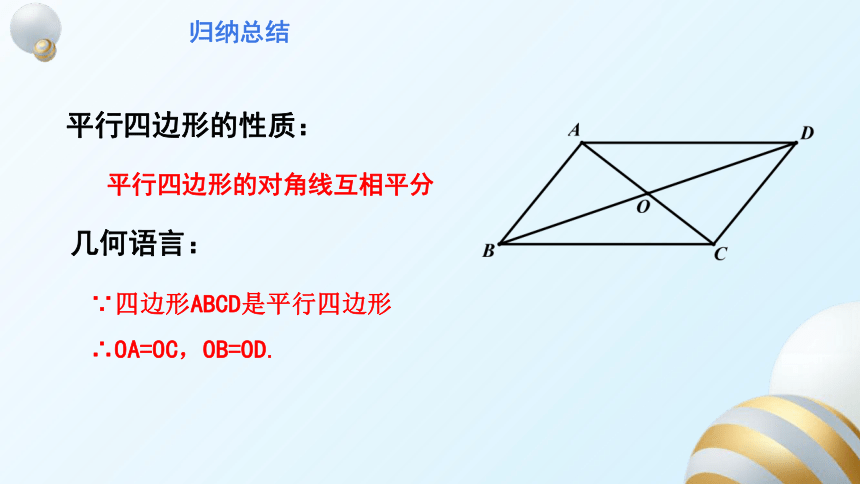
归纳总结
平行四边形的性质:
平行四边形的对角线互相平分
几何语言:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD.
新知应用
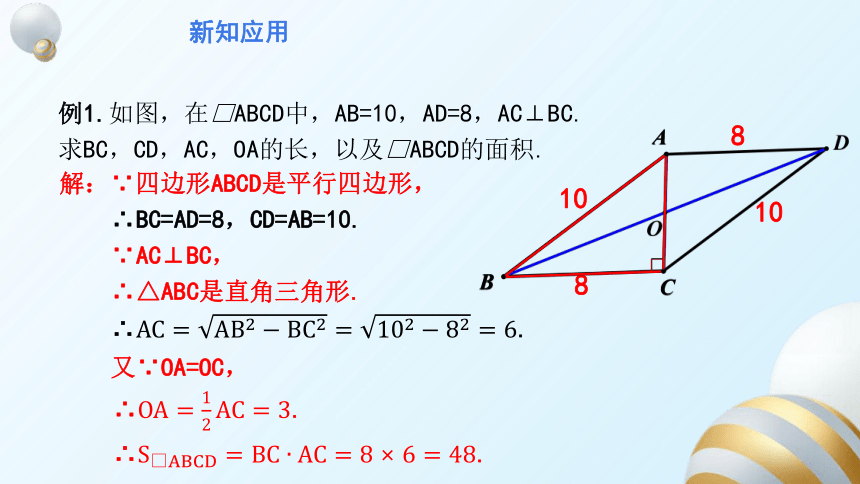
例1.如图,在□ABCD中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及□ABCD的面积.
10
8
8
10
解:∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC,
∴△ABC是直角三角形.
∴.
又∵OA=OC,
∴.
∴.
新知应用
例2:如图,在 ABCD中,BC=10,AC=8,BD=14.△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
A
B
C
D
O
解:∵四边形ABCD是平行四边形,BC=10,AC=8,BD=14
∴AO=CO=AC=4
BO=D0=BD=7
∴△AOD的周长=4+7+10=21
∴△DBC的周长=BD+BC+CD=BD+BC+AB
=14+10+AB=24+AB
∴△ABC的周长=BC+AC+AB
=10+8+AB=18+AB
∵24+AB>18+AB
∴△DBC的周长比△ABC的周长长
∵(24+AB)-(18+AB)=24-18=6
∴△DBC的周长比△ABC的周长长6
新知应用
例3:如图, ABCD的对角线AC,BD相较于点O,EF过点O且与AB,CD分别相交于点E,F。求证OE=OF。
A
B
D
C
E
F
解:∵四边形ABCD是平行四边形
∴OA=OC,AD∥BC
在△OAE和△OCF中
O
∴
∠OAE=∠OCF
OA=OC
∠AOE=∠COF
∴△AOE
∴OE=OF
课堂总结
平行四边形的性质
平行四边形的对角线互相平分
几何语言
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD.
课后练习
课后练习
A
课后练习
D
课后练习
课后练习
课后练习
18.1.1平行四边形的性质2
人教版八年级下册
第18章平行四边形
18.1.1平行四边形的性质2
人教版八年级下册
第18章平行四边形
01
理掌握平行四边形对角线互相平分的性质。
02
能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题。
教学目标
复习回顾
B
A
C
D
∵如图,ABCD为平行四边形
∴AB= AD=
复习一:
∠A= ∠B=
CD
BC
∠C
∠D
复习二:
平行四边形的性质:
平行四边形的对边相等;
平行四边形的对角相等。
新知探究
探究:
上面我们研究了平行四边形的边、角这两个基本要素的性质,下面我们研究平行四边形对角线的性质。
如图,在 ABCD中,连接AC,BD,并设它们相交于点O.OA与OC,OB与OD有什么关系?(请动手画一画,量一量)
D
A
B
D
O
猜想:在 ABCD中,OA=OC,OB=OD
新知探究
验证:
四边形问题
三角形问题
如图,在 ABCD中,对角线AC,BD 相交于点O,
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
证明:∵四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ △COD≌△AOB.
∴ OA=OC,OB=OD.
归纳总结
平行四边形的性质:
平行四边形的对角线互相平分
几何语言:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD.
新知应用
例1.如图,在□ABCD中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及□ABCD的面积.
10
8
8
10
解:∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC,
∴△ABC是直角三角形.
∴.
又∵OA=OC,
∴.
∴.
新知应用
例2:如图,在 ABCD中,BC=10,AC=8,BD=14.△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
A
B
C
D
O
解:∵四边形ABCD是平行四边形,BC=10,AC=8,BD=14
∴AO=CO=AC=4
BO=D0=BD=7
∴△AOD的周长=4+7+10=21
∴△DBC的周长=BD+BC+CD=BD+BC+AB
=14+10+AB=24+AB
∴△ABC的周长=BC+AC+AB
=10+8+AB=18+AB
∵24+AB>18+AB
∴△DBC的周长比△ABC的周长长
∵(24+AB)-(18+AB)=24-18=6
∴△DBC的周长比△ABC的周长长6
新知应用
例3:如图, ABCD的对角线AC,BD相较于点O,EF过点O且与AB,CD分别相交于点E,F。求证OE=OF。
A
B
D
C
E
F
解:∵四边形ABCD是平行四边形
∴OA=OC,AD∥BC
在△OAE和△OCF中
O
∴
∠OAE=∠OCF
OA=OC
∠AOE=∠COF
∴△AOE
∴OE=OF
课堂总结
平行四边形的性质
平行四边形的对角线互相平分
几何语言
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD.
课后练习
课后练习
A
课后练习
D
课后练习
课后练习
课后练习
18.1.1平行四边形的性质2
人教版八年级下册
第18章平行四边形
