2021-2022学年人教版七年级数学下册5.2.2平行线的判定提高练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.2平行线的判定提高练习 (word版含答案) |

|
|
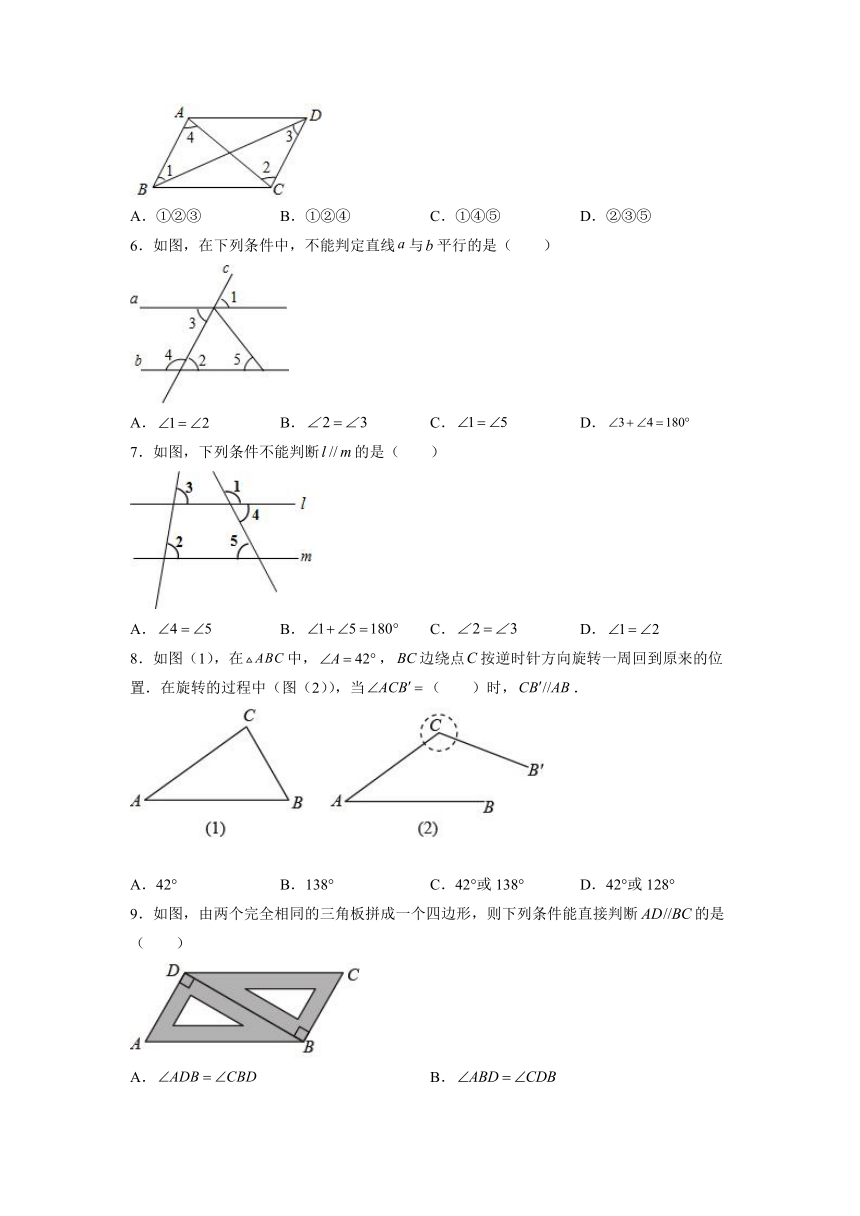
| 格式 | docx | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 09:16:29 | ||
图片预览

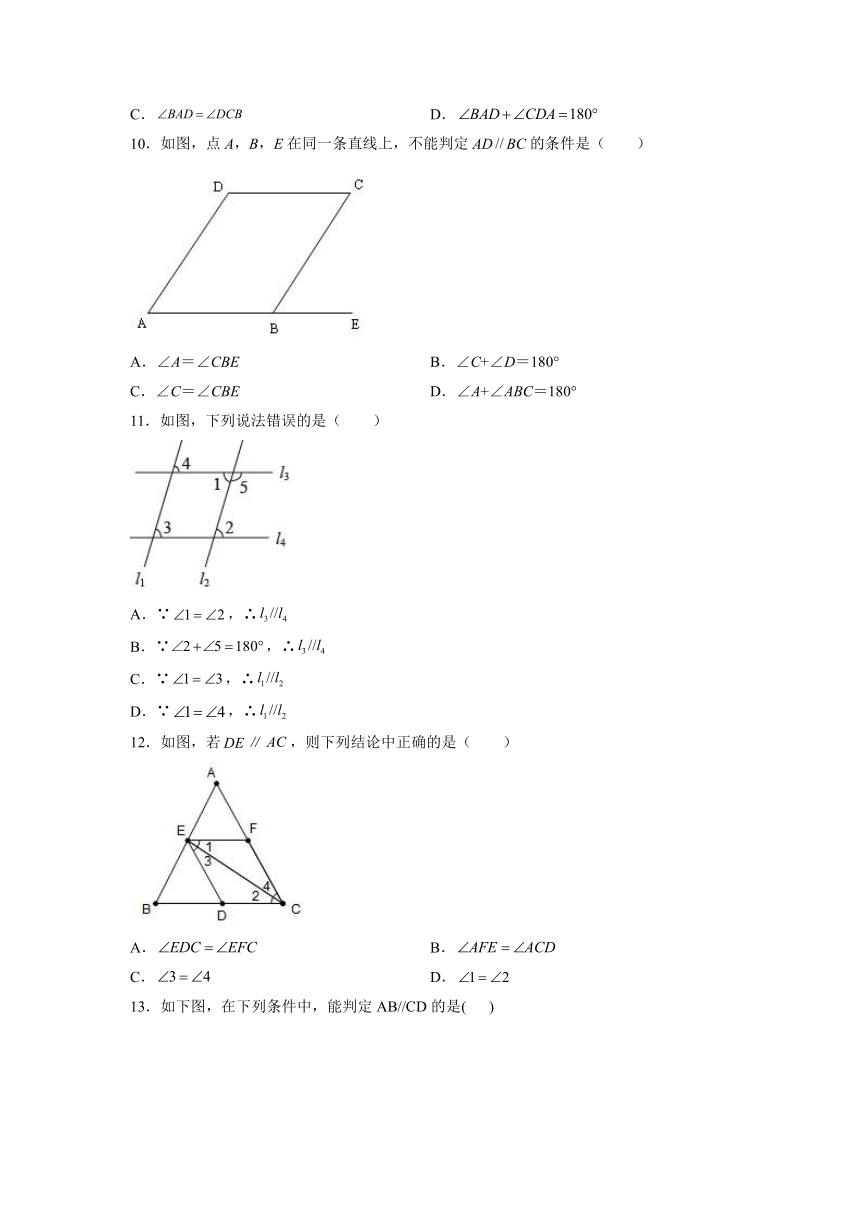
文档简介
5.2.2平行线的判定提高练习
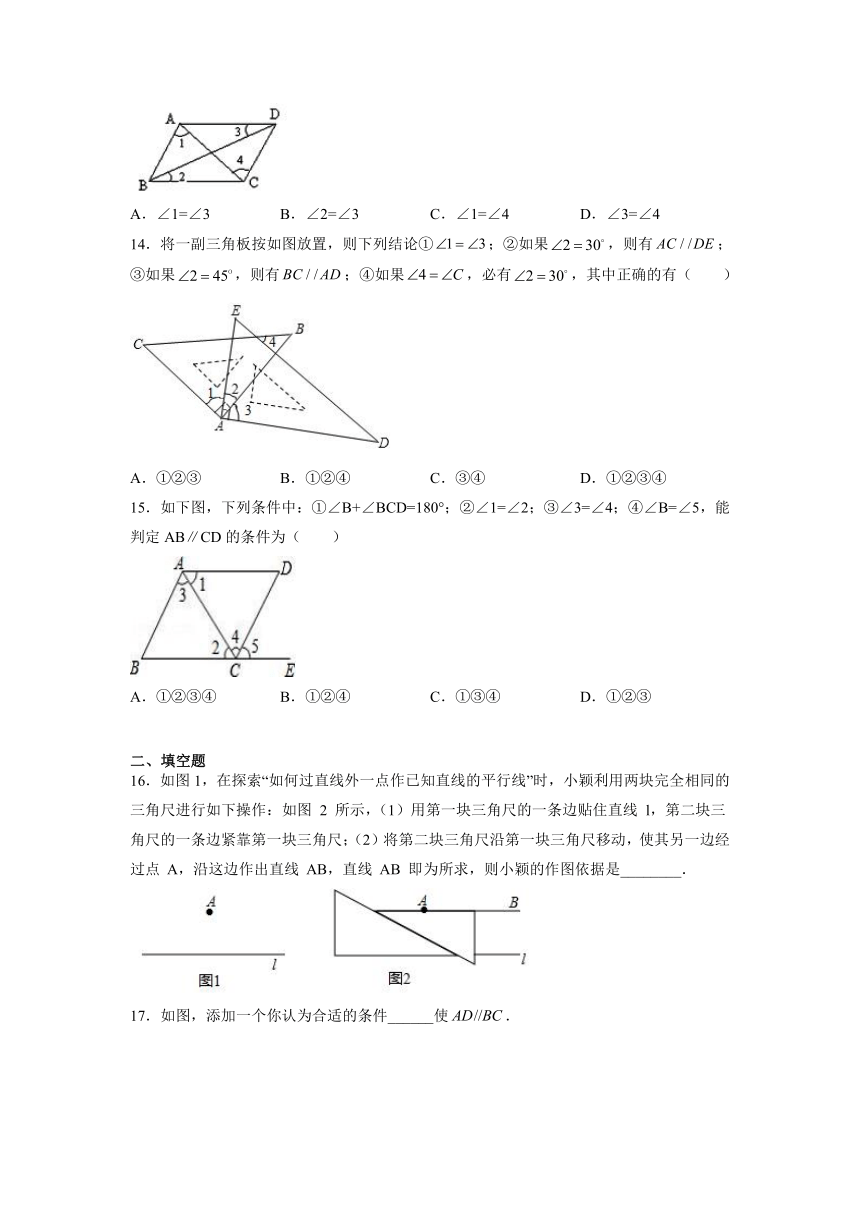
2021--2022学年人教版七年级数学下册
一、单选题
1.下列说法错误的是( )
A.过任意一点可作已知直线的一条平行线 B.同一平面内的两条不相交的直线是平行线
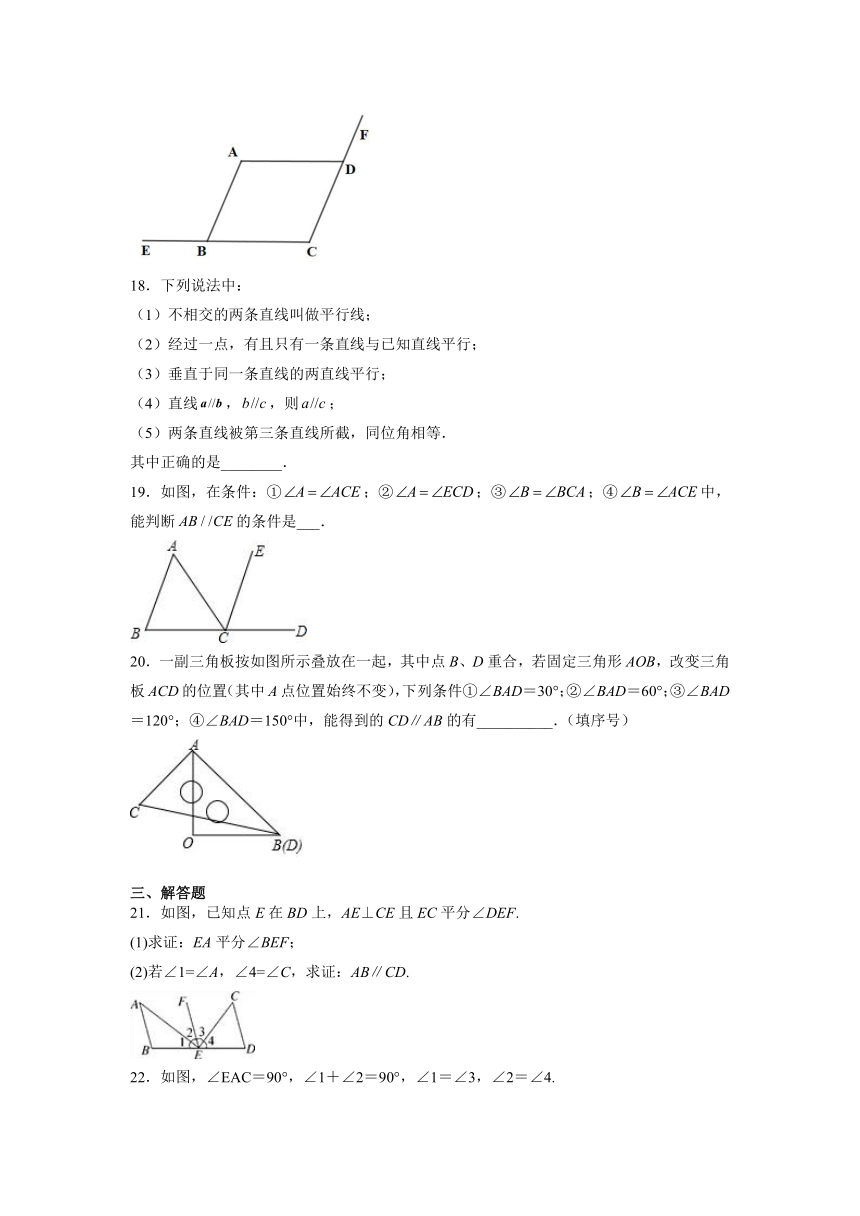
C.过直线外一点只能画一条直线与已知直线平行 D.平行于同一条直线的两条直线平行
2.如图,,C点在EF上,,BC平分,且.下列结论:
①AC平分;②;③;④.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法不正确的是( )
A.同一平面上的两条直线不平行就相交 B.同位角相等,两直线平行
C.过直线外一点只有一条直线与已知直线平行 D.同位角互补,两直线平行
4.如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使,其画法的依据是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.两直线平行,同位角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
5.如图,在下列给出的条件中,可以判定的有( )
①;②;③;④;⑤.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
6.如图,在下列条件中,不能判定直线与平行的是( )
A. B. C. D.
7.如图,下列条件不能判断的是( )
A. B. C. D.
8.如图(1),在中,,边绕点按逆时针方向旋转一周回到原来的位置.在旋转的过程中(图(2)),当( )时,.
A.42° B.138° C.42°或138° D.42°或128°
9.如图,由两个完全相同的三角板拼成一个四边形,则下列条件能直接判断的是( )
A. B.
C. D.
10.如图,点A,B,E在同一条直线上,不能判定ADBC的条件是( )
A.∠A=∠CBE B.∠C+∠D=180°
C.∠C=∠CBE D.∠A+∠ABC=180°
11.如图,下列说法错误的是( )
A.∵,∴
B.∵,∴
C.∵,∴
D.∵,∴
12.如图,若∥,则下列结论中正确的是( )
A. B.
C. D.
13.如下图,在下列条件中,能判定AB//CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
14.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
15.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
二、填空题
16.如图1,在探索“如何过直线外一点作已知直线的平行线”时,小颖利用两块完全相同的三角尺进行如下操作:如图 2 所示,(1)用第一块三角尺的一条边贴住直线 l,第二块三角尺的一条边紧靠第一块三角尺;(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点 A,沿这边作出直线 AB,直线 AB 即为所求,则小颖的作图依据是________.
17.如图,添加一个你认为合适的条件______使.
18.下列说法中:
(1)不相交的两条直线叫做平行线;
(2)经过一点,有且只有一条直线与已知直线平行;
(3)垂直于同一条直线的两直线平行;
(4)直线,,则;
(5)两条直线被第三条直线所截,同位角相等.
其中正确的是________.
19.如图,在条件:①;②;③;④中,能判断的条件是___.
20.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),下列条件①∠BAD=30°;②∠BAD=60°;③∠BAD=120°;④∠BAD=150°中,能得到的CD∥AB的有__________.(填序号)
三、解答题
21.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
22.如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠BFG=∠AEM,求证:AB∥CD.(完成下列填空)
证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC( )
∴∠BEC=∠BFG(等量代换)
∴MC∥ ( )
∴∠C=∠FGD( )
∵∠C=∠EFG(已知)
∴∠ =∠EFG,(等量代换)
∴AB∥CD( )
24.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
25.已知:三角形ABC和三角形DEF位于直线MN的两侧中,直线MN经过点C,且,其中,,,点E、F均落在直线MN上.
(1)如图1,当点C与点E重合时,求证:;聪明的小丽过点C作,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.
(2)将三角形DEF沿着NM的方向平移,如图2,求证:;
(3)将三角形DEF沿着NM的方向平移,使得点E移动到点,画出平移后的三角形DEF,并回答问题,若,则________.(用含的代数式表示)
参考答案
1--10ADDCD CDCAC 11--15CCCDC
16.内错角相等,两直线平行
17.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
18.(4)
19.①
20.①④
21.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°.
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF.
(2)∵AE⊥CE,
∴∠AEC=90°,
∴∠1+∠4=90°.
∵∠1=∠A,∠4=∠C,
∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,
∴AB∥CD.
22(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
23.证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC(对顶角相等)
∴∠BEC=∠BFG(等量代换)
∴MC∥GF(同位角相等,两直线平行)
∴∠C=∠FGD( 两直线平行,同位角相等)
∵∠C=∠EFG(已知)
∴∠FGD=∠EFG,(等量代换)
∴AB∥CD(内错角相等,两直线平行).
故答案是:对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行.
24.解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
25.解:(1)过点C作,
,
,
,
,
,
,
,
,
;
(2)解:,,
又,
,
,
,
,
,
;
(3)如图三角形DEF即为所求作三角形.
∵,
∴,
由(2)得,DE∥AC,
∴∠DEF=∠ECA=,
∵,
∴∠ACB=,
∴ ,
∴∠A=180°-=.
故答案为为:.
2021--2022学年人教版七年级数学下册
一、单选题
1.下列说法错误的是( )
A.过任意一点可作已知直线的一条平行线 B.同一平面内的两条不相交的直线是平行线
C.过直线外一点只能画一条直线与已知直线平行 D.平行于同一条直线的两条直线平行
2.如图,,C点在EF上,,BC平分,且.下列结论:
①AC平分;②;③;④.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法不正确的是( )
A.同一平面上的两条直线不平行就相交 B.同位角相等,两直线平行
C.过直线外一点只有一条直线与已知直线平行 D.同位角互补,两直线平行
4.如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使,其画法的依据是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.两直线平行,同位角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
5.如图,在下列给出的条件中,可以判定的有( )
①;②;③;④;⑤.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
6.如图,在下列条件中,不能判定直线与平行的是( )
A. B. C. D.
7.如图,下列条件不能判断的是( )
A. B. C. D.
8.如图(1),在中,,边绕点按逆时针方向旋转一周回到原来的位置.在旋转的过程中(图(2)),当( )时,.
A.42° B.138° C.42°或138° D.42°或128°
9.如图,由两个完全相同的三角板拼成一个四边形,则下列条件能直接判断的是( )
A. B.
C. D.
10.如图,点A,B,E在同一条直线上,不能判定ADBC的条件是( )
A.∠A=∠CBE B.∠C+∠D=180°
C.∠C=∠CBE D.∠A+∠ABC=180°
11.如图,下列说法错误的是( )
A.∵,∴
B.∵,∴
C.∵,∴
D.∵,∴
12.如图,若∥,则下列结论中正确的是( )
A. B.
C. D.
13.如下图,在下列条件中,能判定AB//CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
14.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
15.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
二、填空题
16.如图1,在探索“如何过直线外一点作已知直线的平行线”时,小颖利用两块完全相同的三角尺进行如下操作:如图 2 所示,(1)用第一块三角尺的一条边贴住直线 l,第二块三角尺的一条边紧靠第一块三角尺;(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点 A,沿这边作出直线 AB,直线 AB 即为所求,则小颖的作图依据是________.
17.如图,添加一个你认为合适的条件______使.
18.下列说法中:
(1)不相交的两条直线叫做平行线;
(2)经过一点,有且只有一条直线与已知直线平行;
(3)垂直于同一条直线的两直线平行;
(4)直线,,则;
(5)两条直线被第三条直线所截,同位角相等.
其中正确的是________.
19.如图,在条件:①;②;③;④中,能判断的条件是___.
20.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),下列条件①∠BAD=30°;②∠BAD=60°;③∠BAD=120°;④∠BAD=150°中,能得到的CD∥AB的有__________.(填序号)
三、解答题
21.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
22.如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠BFG=∠AEM,求证:AB∥CD.(完成下列填空)
证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC( )
∴∠BEC=∠BFG(等量代换)
∴MC∥ ( )
∴∠C=∠FGD( )
∵∠C=∠EFG(已知)
∴∠ =∠EFG,(等量代换)
∴AB∥CD( )
24.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
25.已知:三角形ABC和三角形DEF位于直线MN的两侧中,直线MN经过点C,且,其中,,,点E、F均落在直线MN上.
(1)如图1,当点C与点E重合时,求证:;聪明的小丽过点C作,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.
(2)将三角形DEF沿着NM的方向平移,如图2,求证:;
(3)将三角形DEF沿着NM的方向平移,使得点E移动到点,画出平移后的三角形DEF,并回答问题,若,则________.(用含的代数式表示)
参考答案
1--10ADDCD CDCAC 11--15CCCDC
16.内错角相等,两直线平行
17.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
18.(4)
19.①
20.①④
21.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°.
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF.
(2)∵AE⊥CE,
∴∠AEC=90°,
∴∠1+∠4=90°.
∵∠1=∠A,∠4=∠C,
∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,
∴AB∥CD.
22(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
23.证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC(对顶角相等)
∴∠BEC=∠BFG(等量代换)
∴MC∥GF(同位角相等,两直线平行)
∴∠C=∠FGD( 两直线平行,同位角相等)
∵∠C=∠EFG(已知)
∴∠FGD=∠EFG,(等量代换)
∴AB∥CD(内错角相等,两直线平行).
故答案是:对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行.
24.解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
25.解:(1)过点C作,
,
,
,
,
,
,
,
,
;
(2)解:,,
又,
,
,
,
,
,
;
(3)如图三角形DEF即为所求作三角形.
∵,
∴,
由(2)得,DE∥AC,
∴∠DEF=∠ECA=,
∵,
∴∠ACB=,
∴ ,
∴∠A=180°-=.
故答案为为:.
