人教版 数学六年级下册《抽屉原理》 课件 (共40张PPT)
文档属性
| 名称 | 人教版 数学六年级下册《抽屉原理》 课件 (共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 18:14:07 | ||
图片预览






文档简介
(共40张PPT)
义务课程标准实验教科书六年级数学下册
抽屉原理
学校: 教师:
第五单元
说课流程
抽屉原理
教材分析
学情学法
教学模式
教学设计
板书设计
评价建议
资源开发
六年级
上、下册
四年级
上、下册
五年级
上、下册
植树问题、
时间的统筹、
对策论 。
数字编码 、
找次品 。
鸡兔同笼 、
抽屉原理。
每册一个不同的知识,
用来解决不同的生活实际问题。
本套教材数学广角
的编排特点
一、教材分析
练习十二习题
求至少数
求物体数
例2物体数是抽屉数的多倍多1
例1物体数是抽屉数的1倍多1
例3建抽屉模型
逆向求物体数
1题花色做抽屉
2题5镖5个抽屉
3题颜色当抽屉
六下第五单元
数学广角
4题颜色当抽屉
教材内容
负 数
圆柱与圆锥
比 例
统 计
数学广角
整理和复习
六下数学
一、教材分析
课程目标
1. 在探索过程中经历画图、实物操作,体验数学兴趣 。
2.构建模型,将具体问题数学化,解决生活中实际问题。
3.培养学生逻辑思维能力,和推理能力培养数学兴趣。
1、通过直观例子,借助实际操作,向学生介绍“抽屉原理”。
2、对简单的实际问题加以“模型化”,会用抽屉原理加以解决。
3、抽屉原理是千变万化的,在数论、集合论、组合论中都得到广泛的应用。
单元目标
一、教材分析
依据课程目标和单元目标,确定
理解“抽屉原理”的一般形式。
2.经历“抽屉原理”的探究过程,体会比较、推理的学习方法 。
3.会用“抽屉原理”解决简单的实际问题。
4.感受数学的魅力,提高学习兴趣,培养学生的探究精神。
一、教材分析
教学重点、难点
教学重点
教学难点
本课目标
1、年龄特点:六年级学生既好动又内敛,教师一方面要适当引导,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要创造条件和机会,让学生发表见解,发挥学生学习的主体性。
2、思维特点:知识掌握上,六年级的学生对于总结规律的方法接触比较少,尤其对于“数学证明”。因此教师要耐心细致的引导,重在让学生经历知识发生、发展的过程,而不是生搬硬套,只求结论,要让学生不但知其然,更要知其所以然。
二、学情学法
3、学法上主要采用了自主合作、探究交流的学习方式。体现数学知识的形成过程,让学生在自己的经验中通过观察,实验,猜测,交流等数学活动形成良好的数学思维习惯,提高解决问题的能力,感受数学学习的乐趣。
二、学情学法
导入新课,明确目标
合作探究、理解抽屉原理
重点突破,
总结规律
构建模型,解决问题
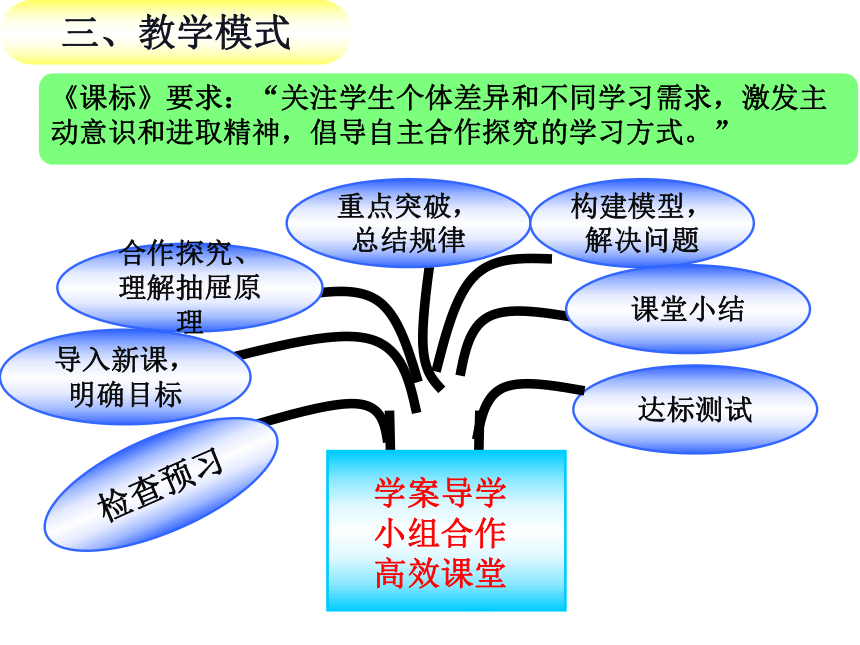
《课标》要求:“关注学生个体差异和不同学习需求,激发主动意识和进取精神,倡导自主合作探究的学习方式。”
三、教学模式
达标测试
课堂模式
学案导学
小组合作
高效课堂
课堂小结
检查预习
(一)检查预习。 (预设时间3分钟)
(二)导入新课,明确目标。 (预设时间1分钟)
(三)小组合作,探究新知 (预设时间15分钟)
(四)重点突破,总结规律。(预设时间6分钟)
(五)构建模型,解决问题。(预设时间4分钟)
(六)课堂小结。 (预设时间2分钟)
(七)达标测试。 (预设时间8分钟)
抽 届 原 理
四、教学设计
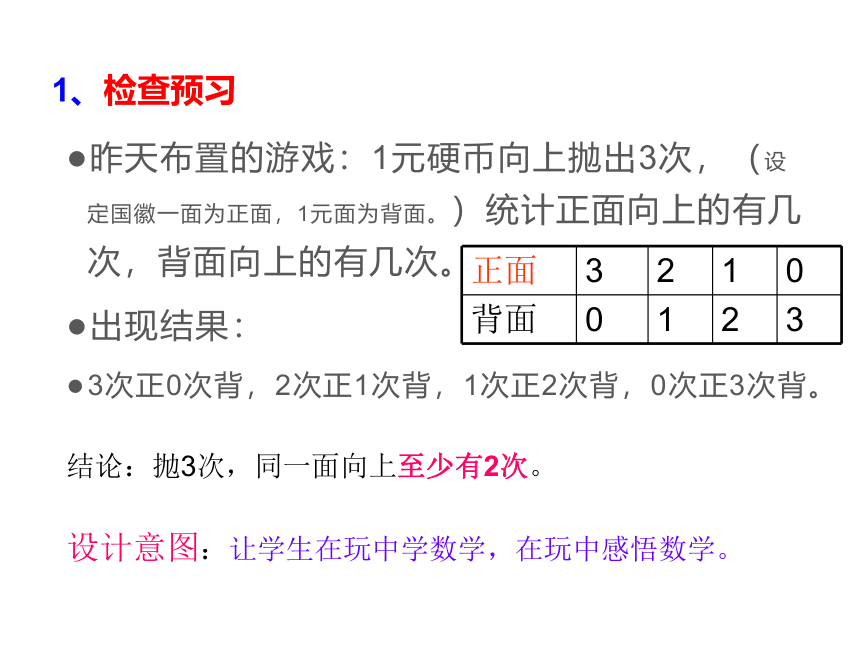
1、检查预习
昨天布置的游戏:1元硬币向上抛出3次,(设定国徽一面为正面,1元面为背面。)统计正面向上的有几次,背面向上的有几次。
出现结果:
3次正0次背,2次正1次背,1次正2次背,0次正3次背。
正面 3 2 1 0
背面 0 1 2 3
结论:抛3次,同一面向上至少有2次。
设计意图:让学生在玩中学数学,在玩中感悟数学。
抽屉原理
2、导入新课、明确目标
理解“抽屉原理”的一般形式。
2.经历“抽屉原理”的探究过程,体会比较、推理的学习方法 。
3.会用“抽屉原理”解决简单的实际问题。
4.感受数学的魅力,提高学习兴趣,培养学生的探究精神。
2导入新课,明确目标
教学重点、难点
教学重点
教学难点
本课目标
仔细观察哦!
小组汇报
仔细观察哦!
小组汇报
仔细观察哦!
小组汇报
仔细观察哦!
小组汇报
共有四种法
小组汇报
猜测:将4根小棒放到3个杯里呢?如何来验证你的结论呢?小组内讨论。
图示法 (刚才课件演示)
列表法 (刚才抛硬币)
组数法:
4=4+0+0, 4=3+1+0, 4=2+2+0, 4=2+1+1.
除法: 4÷3=1(根)…1(根) 1+1=2(根)
师:你为什么用4÷3呢?能解释一下吗?
(学生台前演示) 先将其中的3根小棒分别放到3个杯中,还剩一根,这一根不论放到哪个杯中,那个杯中都至少有两根小棒。用平均分的方法。
小组汇报
解 疑:
老师有个疑问:为什么要平均分呢? (只有平均分,才能保证每个杯中的小棒数是最少的。) 我们用算式表示就是: 4÷3=1(根)……1(根)表示每个杯中先平均放1根,剩下的1根不论放到哪个杯中,总有一个杯中至少有2根小棒。
那将7根小棒放到6个杯中呢?
想一想
7÷6=1(根)……1(根) 1+1=2(根)
●将100根小棒放到99个杯中呢?
100÷99=1(根)……1(根) 1+1=2(根)
你发现了什么规律?同桌说一说。
只要棒数比杯数多1,总有一个杯中至少有2根小棒。
总有一个杯中至少放几根?
重点突破,总结规律
师:刚才研究的问题有个特点:小棒数比杯数多1,有没有想过棒比杯多2、多3、多4的情况?是不是也会有这样的结论呢? 试一试:将5根小棒放到3个杯中;将7根小棒放到4个杯里呢?
(总有一个杯里至少有2根小棒) 不管怎么放,总有一个杯里至少有2根小棒。
设计意图:余数不是1,可用多种方法试验。
重点突破,总结规律
只要小棒比杯子数多,那就总有1个杯子里至少有2根小棒,你同意吗?
例如:9根小棒放到4个杯子里呢?
有1个杯子里至少有3根小棒。
9÷4=2(根)……1(根) 2+1=3(根)
重点突破,总结规律
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
小组交流,你发现了什么规律?
观察今天的板书:
用小棒的数量除以杯子的数量,总有一个杯子里至少有的小棒数就是商加1。
重点突破,总结规律
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
小组交流,你发现了什么规律?
观察今天的板书:
用物体数除以抽屉数,如果能整除总有一个抽屉里至少有商个物体;如果不能整除(有余数)则总有一个抽屉里至少有商+1个物体。
重点突破,总结规律
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
小组交流,你发现了什么规律?
观察今天的板书:
物体数÷抽屉数=商……余数 至少数=商+1(非余数)
物体数÷抽屉数=商 (整除) 至少数=商
重点突破,总结规律
现在你能用这个原理解决问题吗?
构建模型,解决问题
1、
(课本 70页“做一做”)
构建模型,解决问题
2、一幅扑克,拿走大、小王后还有52张牌,任意抽出其中的5张,总会有至少两张牌的花色相同,为什么? (练习12第1题)
构建模型,解决问题
课堂小结:
分清哪是物体,哪是抽屉,这是解决抽屉问题的关键。
物体数÷抽屉数==商……余数
至少数==商+1(非余数)(有余数时)
达标测试:
A、填空:
(1)5本书分给4个小朋友,至少有( )本书要在同一个小朋友手里。
(2)6只小松鼠摘了10个松果,采得最多的那只小松鼠至少有( )松果。
(3)将15个苹果放到4个盘子中,总会有一个盘子至少有( )个苹果。
达标测试:
B、选择:
(1)王东玩掷骰子游戏,掷出7次,至少有( )次相同。
a、6 b、2 c、7 d、1
(2)7只兔子要装进6个笼子,至少有( )只兔子要装进同一个笼里。
a、6 b、2 c、7 d、1
达标测试:
C、判断:
(1)明明把13张邮票送给5个小朋友,至少有7张邮票要在同一个小朋友手里。 ( )
(2)14个朋友做了30朵红花,至少有两个小朋友要做完4朵红花。 ( )
达标测试:
D、解决问题:
我们班共65人,至少几个人的属相相同?为什么?
五、板书设计
数学广角——抽屉原理
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
物体数÷抽屉数=商……余数 至少数=商+1
物体数÷抽屉数=商 (整除) 至少数=商
六、评价建议
知识与能力
过程与方法
情感态度价值观
全面考察学生的数学素养。
评价建议
形成性、终结性评价要及时,重视形成性评价。知识堂堂清,人人清
整体性和
综合性
评价方式多样
定性与定量
评价主体的多元与互动
重视定性
客观描述
鼓励表扬
重视定性评价。
教师评价
学生互评
学生自评
六、评价建议
评价及时,伴随课堂每一步
1、预习完成好的作业在教室展览。
2、小组合作探究方法正确的,让该小组汇报体验成功感。
3、实际操作摆放全面的,让代表台前展示,经历操作的喜悦。
4、规律总结严紧的,让他口述总结,体现逻辑思维能力。
5、课堂练习完成快又准的,给予书面百分制评价。
6、学生自评和互评。
7、家长参与的作业评价。
展示教师
资源
利用教材
资源
挖掘学生
资源
多媒体资源
开发和利用课程资源
社会资源
开发课外
资源
利用课内资源
学校资源
各大教育网站
七、资源开发
设计意图:课标要求:“数学教师要高度重视课程资源的开发和利用,增强学生在生活中用数学知识的意识” 。
谢谢
义务课程标准实验教科书六年级数学下册
抽屉原理
学校: 教师:
第五单元
说课流程
抽屉原理
教材分析
学情学法
教学模式
教学设计
板书设计
评价建议
资源开发
六年级
上、下册
四年级
上、下册
五年级
上、下册
植树问题、
时间的统筹、
对策论 。
数字编码 、
找次品 。
鸡兔同笼 、
抽屉原理。
每册一个不同的知识,
用来解决不同的生活实际问题。
本套教材数学广角
的编排特点
一、教材分析
练习十二习题
求至少数
求物体数
例2物体数是抽屉数的多倍多1
例1物体数是抽屉数的1倍多1
例3建抽屉模型
逆向求物体数
1题花色做抽屉
2题5镖5个抽屉
3题颜色当抽屉
六下第五单元
数学广角
4题颜色当抽屉
教材内容
负 数
圆柱与圆锥
比 例
统 计
数学广角
整理和复习
六下数学
一、教材分析
课程目标
1. 在探索过程中经历画图、实物操作,体验数学兴趣 。
2.构建模型,将具体问题数学化,解决生活中实际问题。
3.培养学生逻辑思维能力,和推理能力培养数学兴趣。
1、通过直观例子,借助实际操作,向学生介绍“抽屉原理”。
2、对简单的实际问题加以“模型化”,会用抽屉原理加以解决。
3、抽屉原理是千变万化的,在数论、集合论、组合论中都得到广泛的应用。
单元目标
一、教材分析
依据课程目标和单元目标,确定
理解“抽屉原理”的一般形式。
2.经历“抽屉原理”的探究过程,体会比较、推理的学习方法 。
3.会用“抽屉原理”解决简单的实际问题。
4.感受数学的魅力,提高学习兴趣,培养学生的探究精神。
一、教材分析
教学重点、难点
教学重点
教学难点
本课目标
1、年龄特点:六年级学生既好动又内敛,教师一方面要适当引导,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要创造条件和机会,让学生发表见解,发挥学生学习的主体性。
2、思维特点:知识掌握上,六年级的学生对于总结规律的方法接触比较少,尤其对于“数学证明”。因此教师要耐心细致的引导,重在让学生经历知识发生、发展的过程,而不是生搬硬套,只求结论,要让学生不但知其然,更要知其所以然。
二、学情学法
3、学法上主要采用了自主合作、探究交流的学习方式。体现数学知识的形成过程,让学生在自己的经验中通过观察,实验,猜测,交流等数学活动形成良好的数学思维习惯,提高解决问题的能力,感受数学学习的乐趣。
二、学情学法
导入新课,明确目标
合作探究、理解抽屉原理
重点突破,
总结规律
构建模型,解决问题
《课标》要求:“关注学生个体差异和不同学习需求,激发主动意识和进取精神,倡导自主合作探究的学习方式。”
三、教学模式
达标测试
课堂模式
学案导学
小组合作
高效课堂
课堂小结
检查预习
(一)检查预习。 (预设时间3分钟)
(二)导入新课,明确目标。 (预设时间1分钟)
(三)小组合作,探究新知 (预设时间15分钟)
(四)重点突破,总结规律。(预设时间6分钟)
(五)构建模型,解决问题。(预设时间4分钟)
(六)课堂小结。 (预设时间2分钟)
(七)达标测试。 (预设时间8分钟)
抽 届 原 理
四、教学设计
1、检查预习
昨天布置的游戏:1元硬币向上抛出3次,(设定国徽一面为正面,1元面为背面。)统计正面向上的有几次,背面向上的有几次。
出现结果:
3次正0次背,2次正1次背,1次正2次背,0次正3次背。
正面 3 2 1 0
背面 0 1 2 3
结论:抛3次,同一面向上至少有2次。
设计意图:让学生在玩中学数学,在玩中感悟数学。
抽屉原理
2、导入新课、明确目标
理解“抽屉原理”的一般形式。
2.经历“抽屉原理”的探究过程,体会比较、推理的学习方法 。
3.会用“抽屉原理”解决简单的实际问题。
4.感受数学的魅力,提高学习兴趣,培养学生的探究精神。
2导入新课,明确目标
教学重点、难点
教学重点
教学难点
本课目标
仔细观察哦!
小组汇报
仔细观察哦!
小组汇报
仔细观察哦!
小组汇报
仔细观察哦!
小组汇报
共有四种法
小组汇报
猜测:将4根小棒放到3个杯里呢?如何来验证你的结论呢?小组内讨论。
图示法 (刚才课件演示)
列表法 (刚才抛硬币)
组数法:
4=4+0+0, 4=3+1+0, 4=2+2+0, 4=2+1+1.
除法: 4÷3=1(根)…1(根) 1+1=2(根)
师:你为什么用4÷3呢?能解释一下吗?
(学生台前演示) 先将其中的3根小棒分别放到3个杯中,还剩一根,这一根不论放到哪个杯中,那个杯中都至少有两根小棒。用平均分的方法。
小组汇报
解 疑:
老师有个疑问:为什么要平均分呢? (只有平均分,才能保证每个杯中的小棒数是最少的。) 我们用算式表示就是: 4÷3=1(根)……1(根)表示每个杯中先平均放1根,剩下的1根不论放到哪个杯中,总有一个杯中至少有2根小棒。
那将7根小棒放到6个杯中呢?
想一想
7÷6=1(根)……1(根) 1+1=2(根)
●将100根小棒放到99个杯中呢?
100÷99=1(根)……1(根) 1+1=2(根)
你发现了什么规律?同桌说一说。
只要棒数比杯数多1,总有一个杯中至少有2根小棒。
总有一个杯中至少放几根?
重点突破,总结规律
师:刚才研究的问题有个特点:小棒数比杯数多1,有没有想过棒比杯多2、多3、多4的情况?是不是也会有这样的结论呢? 试一试:将5根小棒放到3个杯中;将7根小棒放到4个杯里呢?
(总有一个杯里至少有2根小棒) 不管怎么放,总有一个杯里至少有2根小棒。
设计意图:余数不是1,可用多种方法试验。
重点突破,总结规律
只要小棒比杯子数多,那就总有1个杯子里至少有2根小棒,你同意吗?
例如:9根小棒放到4个杯子里呢?
有1个杯子里至少有3根小棒。
9÷4=2(根)……1(根) 2+1=3(根)
重点突破,总结规律
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
小组交流,你发现了什么规律?
观察今天的板书:
用小棒的数量除以杯子的数量,总有一个杯子里至少有的小棒数就是商加1。
重点突破,总结规律
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
小组交流,你发现了什么规律?
观察今天的板书:
用物体数除以抽屉数,如果能整除总有一个抽屉里至少有商个物体;如果不能整除(有余数)则总有一个抽屉里至少有商+1个物体。
重点突破,总结规律
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
小组交流,你发现了什么规律?
观察今天的板书:
物体数÷抽屉数=商……余数 至少数=商+1(非余数)
物体数÷抽屉数=商 (整除) 至少数=商
重点突破,总结规律
现在你能用这个原理解决问题吗?
构建模型,解决问题
1、
(课本 70页“做一做”)
构建模型,解决问题
2、一幅扑克,拿走大、小王后还有52张牌,任意抽出其中的5张,总会有至少两张牌的花色相同,为什么? (练习12第1题)
构建模型,解决问题
课堂小结:
分清哪是物体,哪是抽屉,这是解决抽屉问题的关键。
物体数÷抽屉数==商……余数
至少数==商+1(非余数)(有余数时)
达标测试:
A、填空:
(1)5本书分给4个小朋友,至少有( )本书要在同一个小朋友手里。
(2)6只小松鼠摘了10个松果,采得最多的那只小松鼠至少有( )松果。
(3)将15个苹果放到4个盘子中,总会有一个盘子至少有( )个苹果。
达标测试:
B、选择:
(1)王东玩掷骰子游戏,掷出7次,至少有( )次相同。
a、6 b、2 c、7 d、1
(2)7只兔子要装进6个笼子,至少有( )只兔子要装进同一个笼里。
a、6 b、2 c、7 d、1
达标测试:
C、判断:
(1)明明把13张邮票送给5个小朋友,至少有7张邮票要在同一个小朋友手里。 ( )
(2)14个朋友做了30朵红花,至少有两个小朋友要做完4朵红花。 ( )
达标测试:
D、解决问题:
我们班共65人,至少几个人的属相相同?为什么?
五、板书设计
数学广角——抽屉原理
4÷3=1(根)……1(根) 1+1=2(根)
7÷6=1(根)……1(根) 1+1=2(根)
7÷4=1(根)……3(根) 1+1=2(根)
9÷4=2(根)……1(根) 2+1=3(根)
物体数÷抽屉数=商……余数 至少数=商+1
物体数÷抽屉数=商 (整除) 至少数=商
六、评价建议
知识与能力
过程与方法
情感态度价值观
全面考察学生的数学素养。
评价建议
形成性、终结性评价要及时,重视形成性评价。知识堂堂清,人人清
整体性和
综合性
评价方式多样
定性与定量
评价主体的多元与互动
重视定性
客观描述
鼓励表扬
重视定性评价。
教师评价
学生互评
学生自评
六、评价建议
评价及时,伴随课堂每一步
1、预习完成好的作业在教室展览。
2、小组合作探究方法正确的,让该小组汇报体验成功感。
3、实际操作摆放全面的,让代表台前展示,经历操作的喜悦。
4、规律总结严紧的,让他口述总结,体现逻辑思维能力。
5、课堂练习完成快又准的,给予书面百分制评价。
6、学生自评和互评。
7、家长参与的作业评价。
展示教师
资源
利用教材
资源
挖掘学生
资源
多媒体资源
开发和利用课程资源
社会资源
开发课外
资源
利用课内资源
学校资源
各大教育网站
七、资源开发
设计意图:课标要求:“数学教师要高度重视课程资源的开发和利用,增强学生在生活中用数学知识的意识” 。
谢谢
