人教版八年级数学下册18.2.3《正方形》随堂训练 (word版含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2.3《正方形》随堂训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 09:26:36 | ||
图片预览


文档简介
18.2.3《正方形》随堂训练
2021-2022学年人教版八年级数学下册
一、单选题
1.正方形的对角线长为2,则其面积为( )
A.1 B.2 C.3 D.4
2.正方形是轴对称图形,它的对称轴有( )
A.1条 B.2条 C.4条 D.8条
3.已知正方形的对角线相交于点,且,则的长度和的度数分别是( )
A. B. C. D.
4.已知在四边形中,,下列可以判定四边形是正方形的是( )
A. B. C. D.
5.如图,在正方形 中, 是 上的一点,且 ,则 的度数是()
A. B. C. D.
6.如图,将一边长为12的正方形纸片的顶点A折叠至边上的点E,使,若折痕为,则的长为( )
A.13 B.14 C.15 D.16
7.过正方形的中心作两条互相垂直的直线,则以这两条直线与正方形各边交点为顶点的四边形是( )
A.筝形 B.矩形 C.菱形 D.正方形
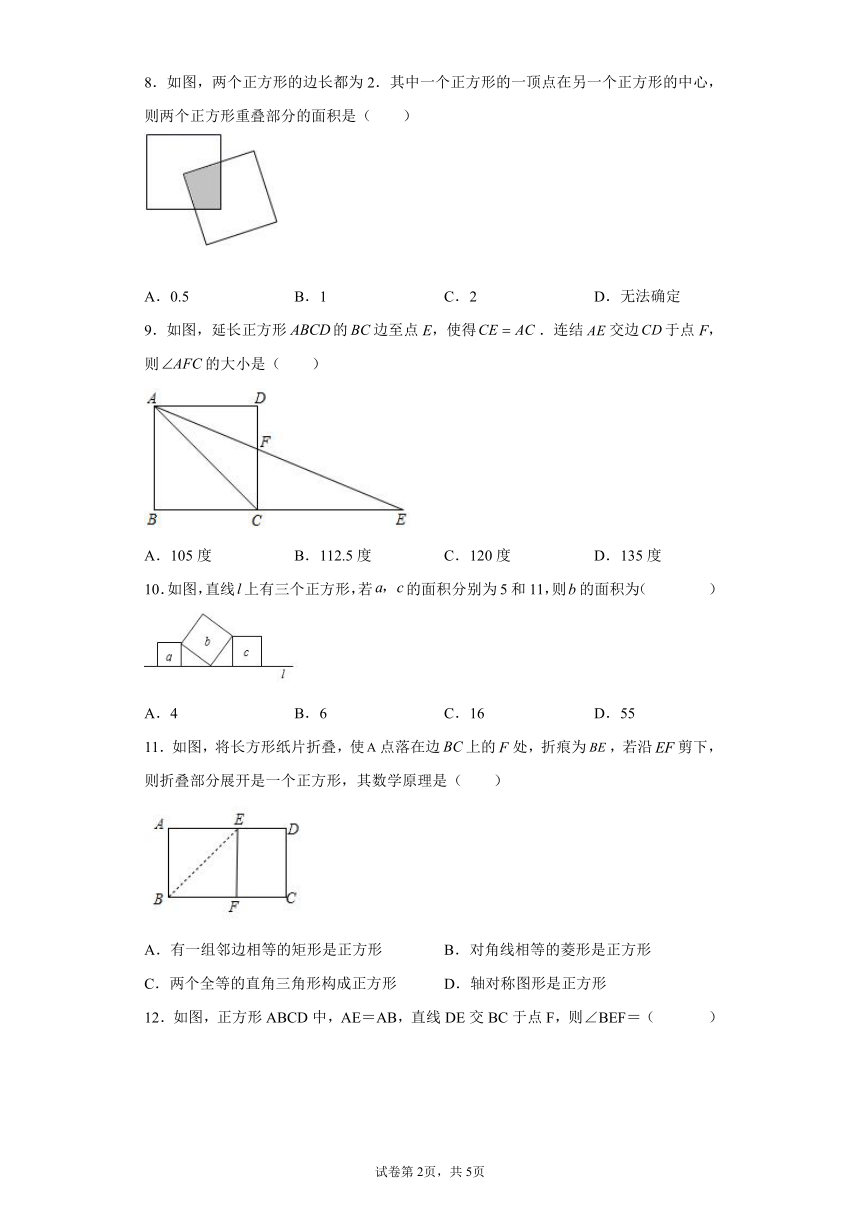
8.如图,两个正方形的边长都为2.其中一个正方形的一顶点在另一个正方形的中心,则两个正方形重叠部分的面积是( )
A.0.5 B.1 C.2 D.无法确定
9.如图,延长正方形的边至点E,使得.连结交边于点F,则的大小是( )
A.105度 B.112.5度 C.120度 D.135度
10.如图,直线上有三个正方形,若的面积分别为5和11,则的面积为( )
A.4 B.6 C.16 D.55
11.如图,将长方形纸片折叠,使点落在边上的处,折痕为,若沿剪下,则折叠部分展开是一个正方形,其数学原理是( )
A.有一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
12.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.45° B.30° C.60° D.55°
二、填空题
13.有一个角是_______的菱形是正方形,对角线_________的菱形是正方形.
14.正方形的四个角________四条边_________,对角线________且互相_______,每条对角线_________一组对角.
15.如图所示,P是正方形ABCD 内一点,将△ABP绕点B按顺时针方向旋转能与△CBP'重合,若PB=3,则PP'=__________
16.边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为_____.
17.在四边形中,,,试补充一个条件__________,使四边形是正方形.
18.如图,正方形的边长为1,E为对角线上一点,,作交于F,则____________.
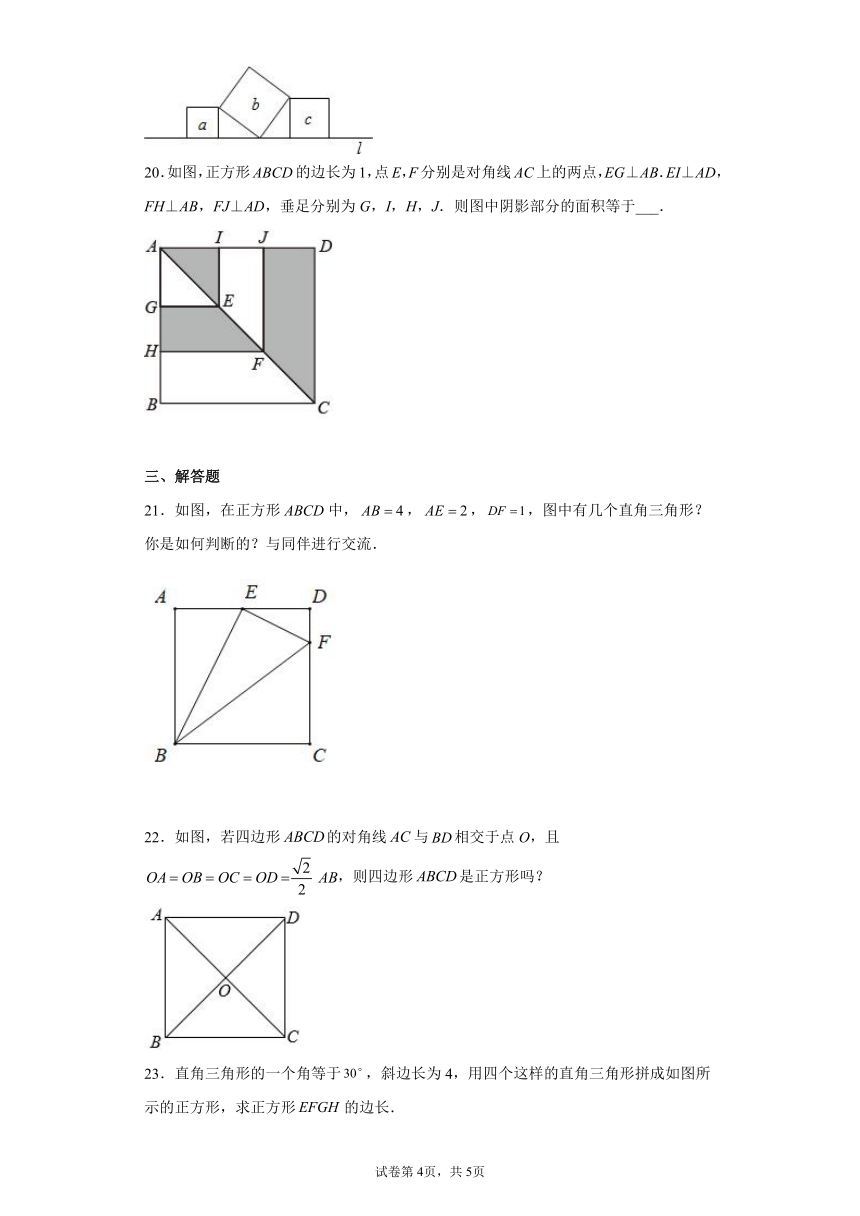
19.如图,直线l上摆有三个正方形a,b,c,若a、c的面积分别为8和10,则b的面积是__________.
20.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于___.
三、解答题
21.如图,在正方形ABCD中,,,,图中有几个直角三角形?你是如何判断的?与同伴进行交流.
22.如图,若四边形的对角线与相交于点O,且,则四边形是正方形吗?
23.直角三角形的一个角等于,斜边长为4,用四个这样的直角三角形拼成如图所示的正方形,求正方形的边长.
24.如图(1),是一张正方形纸片,E,F分别为的中点,沿过点D的折痕将A角翻折,使得点A落在上(如图(2)的点),折痕交于点G,那么等于多少度?你能证明你的结论吗?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
2.C
3.D
4.D
5.B
6.A
7.D
8.B
9.B
10.C
11.A
12.A
13.直角 相等
14.都是直角 都相等 相等 垂直平分 平分
15.3
16.2a2
17.(答案不唯一)
18.
19.18
20.
21.
图中,,分别有一个角为正方形的内角,是直角;
是正方形,
,
,
,,
也是直角三角形
故图中共有个直角三角形.
22.
解:四边形ABCD是正方形,
理由是:∵OA=OB=OC=OD,
∴AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
∵,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形.
23.
解:直角三角形的一个角是,斜边长为4.
.
.
正方形是四个这样的直角三角形拼成的.
.
.
故答案为:.
24
解:如图,连接,
四边形是正方形,
,,,
、分别为、的中点,
,
,
∵,,,
四边形是矩形,
,
,
又∵点是的中点,
∴EF垂直平分CD,
∴,
∵折叠,
∴,,
又∵,
∴,
为等边三角形,
,
,
.
答案第1页,共2页
答案第1页,共2页
2021-2022学年人教版八年级数学下册
一、单选题
1.正方形的对角线长为2,则其面积为( )
A.1 B.2 C.3 D.4
2.正方形是轴对称图形,它的对称轴有( )
A.1条 B.2条 C.4条 D.8条
3.已知正方形的对角线相交于点,且,则的长度和的度数分别是( )
A. B. C. D.
4.已知在四边形中,,下列可以判定四边形是正方形的是( )
A. B. C. D.
5.如图,在正方形 中, 是 上的一点,且 ,则 的度数是()
A. B. C. D.
6.如图,将一边长为12的正方形纸片的顶点A折叠至边上的点E,使,若折痕为,则的长为( )
A.13 B.14 C.15 D.16
7.过正方形的中心作两条互相垂直的直线,则以这两条直线与正方形各边交点为顶点的四边形是( )
A.筝形 B.矩形 C.菱形 D.正方形
8.如图,两个正方形的边长都为2.其中一个正方形的一顶点在另一个正方形的中心,则两个正方形重叠部分的面积是( )
A.0.5 B.1 C.2 D.无法确定
9.如图,延长正方形的边至点E,使得.连结交边于点F,则的大小是( )
A.105度 B.112.5度 C.120度 D.135度
10.如图,直线上有三个正方形,若的面积分别为5和11,则的面积为( )
A.4 B.6 C.16 D.55
11.如图,将长方形纸片折叠,使点落在边上的处,折痕为,若沿剪下,则折叠部分展开是一个正方形,其数学原理是( )
A.有一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
12.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.45° B.30° C.60° D.55°
二、填空题
13.有一个角是_______的菱形是正方形,对角线_________的菱形是正方形.
14.正方形的四个角________四条边_________,对角线________且互相_______,每条对角线_________一组对角.
15.如图所示,P是正方形ABCD 内一点,将△ABP绕点B按顺时针方向旋转能与△CBP'重合,若PB=3,则PP'=__________
16.边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为_____.
17.在四边形中,,,试补充一个条件__________,使四边形是正方形.
18.如图,正方形的边长为1,E为对角线上一点,,作交于F,则____________.
19.如图,直线l上摆有三个正方形a,b,c,若a、c的面积分别为8和10,则b的面积是__________.
20.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于___.
三、解答题
21.如图,在正方形ABCD中,,,,图中有几个直角三角形?你是如何判断的?与同伴进行交流.
22.如图,若四边形的对角线与相交于点O,且,则四边形是正方形吗?
23.直角三角形的一个角等于,斜边长为4,用四个这样的直角三角形拼成如图所示的正方形,求正方形的边长.
24.如图(1),是一张正方形纸片,E,F分别为的中点,沿过点D的折痕将A角翻折,使得点A落在上(如图(2)的点),折痕交于点G,那么等于多少度?你能证明你的结论吗?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
2.C
3.D
4.D
5.B
6.A
7.D
8.B
9.B
10.C
11.A
12.A
13.直角 相等
14.都是直角 都相等 相等 垂直平分 平分
15.3
16.2a2
17.(答案不唯一)
18.
19.18
20.
21.
图中,,分别有一个角为正方形的内角,是直角;
是正方形,
,
,
,,
也是直角三角形
故图中共有个直角三角形.
22.
解:四边形ABCD是正方形,
理由是:∵OA=OB=OC=OD,
∴AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
∵,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形.
23.
解:直角三角形的一个角是,斜边长为4.
.
.
正方形是四个这样的直角三角形拼成的.
.
.
故答案为:.
24
解:如图,连接,
四边形是正方形,
,,,
、分别为、的中点,
,
,
∵,,,
四边形是矩形,
,
,
又∵点是的中点,
∴EF垂直平分CD,
∴,
∵折叠,
∴,,
又∵,
∴,
为等边三角形,
,
,
.
答案第1页,共2页
答案第1页,共2页
