人教版八年级数学下册18.2.2《菱形》随堂训练 (word版含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2.2《菱形》随堂训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 239.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 09:30:13 | ||
图片预览

文档简介
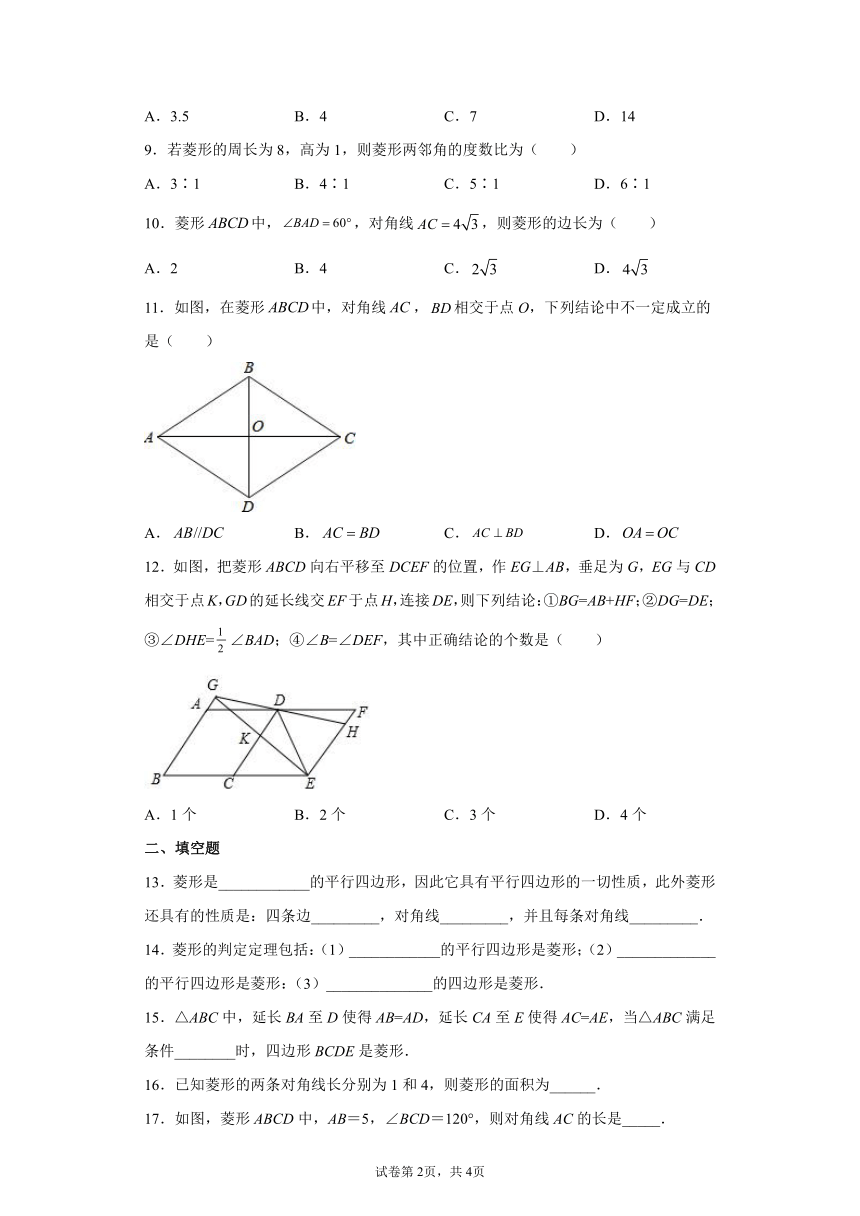
18.2.2《菱形》随堂训练
2021-2022学年人教版八年级数学下册
一、单选题
1.下列各项中,菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.邻边相等 D.对角线相等
2.对角线互相垂直平分的四边形是( )
A.任意四边形 B.筝形 C.矩形 D.菱形
3.在四边形中,对角线,互相平分,若添加一个条件使得四边形是菱形,则这个条件可以是( )
A. B. C. D.
4.菱形的两条对角线分别为和,则它的高为( )
A. B. C. D.
5.菱形中,,若周长为8,则此菱形的高为( )
A.0.5 B.1 C.2 D.4
6.菱形中,对角线交于点O,给出下列结论:①,②,③,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
7.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
A.12 B.16 C.20 D.24
8.如图,菱形中,对角线相交于点O,E为边中点,菱形的周长为28,则的长等于( )
A.3.5 B.4 C.7 D.14
9.若菱形的周长为8,高为1,则菱形两邻角的度数比为( )
A.3∶1 B.4∶1 C.5∶1 D.6∶1
10.菱形中,,对角线,则菱形的边长为( )
A.2 B.4 C. D.
11.如图,在菱形中,对角线,相交于点O,下列结论中不一定成立的是( )
A. B. C. D.
12.如图,把菱形ABCD向右平移至DCEF的位置,作EG⊥AB,垂足为G,EG与CD相交于点K,GD的延长线交EF于点H,连接DE,则下列结论:①BG=AB+HF;②DG=DE;③∠DHE=∠BAD;④∠B=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.菱形是____________的平行四边形,因此它具有平行四边形的一切性质,此外菱形还具有的性质是:四条边_________,对角线_________,并且每条对角线_________.
14.菱形的判定定理包括:(1)____________的平行四边形是菱形;(2)_____________的平行四边形是菱形:(3)______________的四边形是菱形.
15.△ABC中,延长BA至D使得AB=AD,延长CA至E使得AC=AE,当△ABC满足条件________时,四边形BCDE是菱形.
16.已知菱形的两条对角线长分别为1和4,则菱形的面积为______.
17.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是_____.
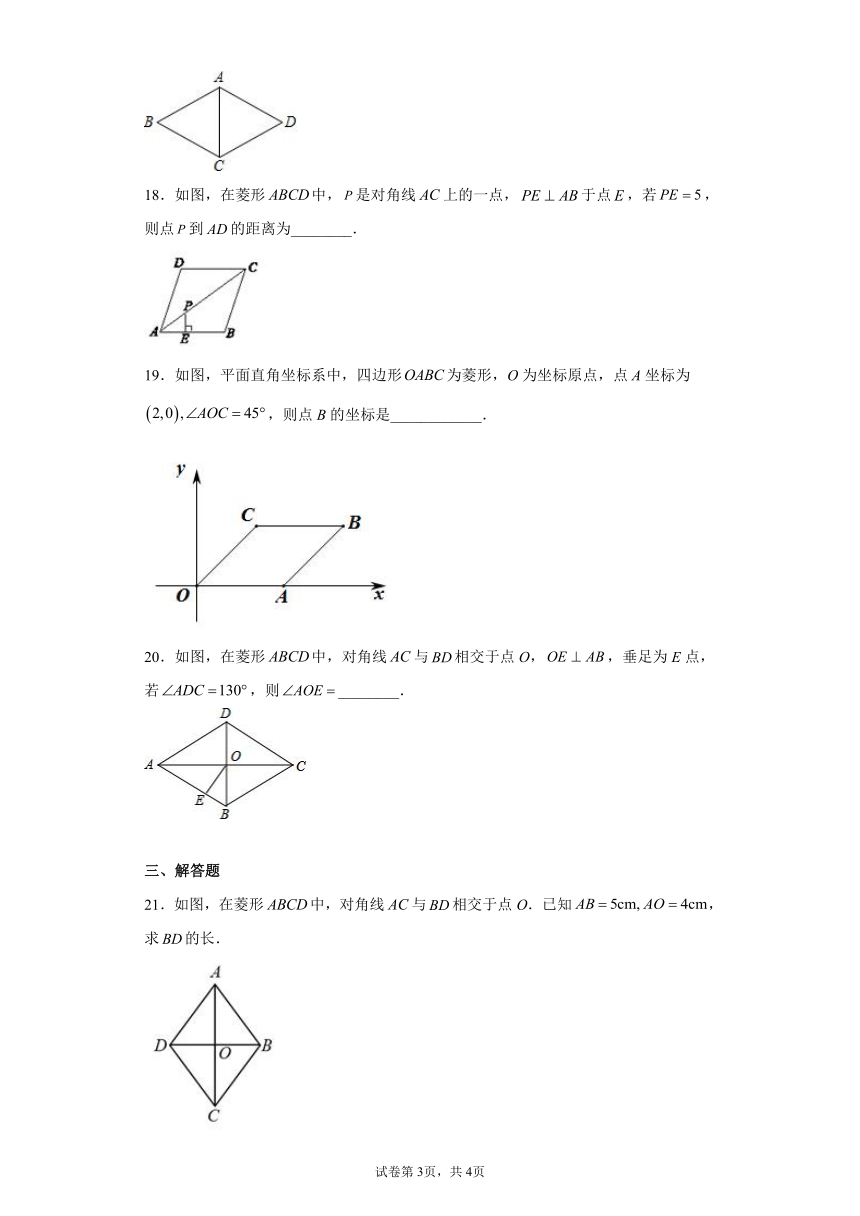
18.如图,在菱形中,是对角线上的一点,于点,若,则点到的距离为________.
19.如图,平面直角坐标系中,四边形为菱形,O为坐标原点,点A坐标为,则点B的坐标是____________.
20.如图,在菱形中,对角线与相交于点O,,垂足为E点,若,则________.
三、解答题
21.如图,在菱形中,对角线与相交于点O.已知,求的长.
22.已知:如图,在菱形中,,对角线与相交于点O.
求证:(1);
(2).
23.如图,四边形是边长为的菱形,其中对角线长.求:
(1)对角线的长度;
(2)菱形的面积.
24.已知:如图,在菱形中,对角线与相交于点O,点E,F,G,H分别是,,,的中点.求证:四边形是菱形.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.D
3.B
4.D
5.B
6.C
7.D
8.A
9.C
10.B
11.B
12.C
13.有一组邻边相等 都相等 互相垂直 平分一组对角
14.有一组邻边相等 对角线互相垂直 四条边都相等
15.∠BAC=90°
16.2
17.5.
18.5
19.
20.65°
21.
解: 菱形中,对角线,相交于点,
,,
,,
,
∴的长为6cm.
22.
证明:(1)∵四边形是菱形,
∴(菱形的对边相等)
又∵,
∴.
(2)∵,
∴是等腰三角形.
又∵四边形是菱形,
∴(菱形的对角线互相平分).
在等腰三角形中,
∵,
∴,
即.
23.
解:(1)∵四边形是菱形,与相交于点E,
∴(菱形的对角线互相垂直),
(菱形的对角线互相平分).
∴.
∴(菱形的对角线互相平分);
(2)
.
24.
证明:、为、的中点,
为的中位线,
,
同理可得:,,,
又四边形为菱形,
,
,
四边形为菱形.
答案第1页,共2页
答案第1页,共2页
2021-2022学年人教版八年级数学下册
一、单选题
1.下列各项中,菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.邻边相等 D.对角线相等
2.对角线互相垂直平分的四边形是( )
A.任意四边形 B.筝形 C.矩形 D.菱形
3.在四边形中,对角线,互相平分,若添加一个条件使得四边形是菱形,则这个条件可以是( )
A. B. C. D.
4.菱形的两条对角线分别为和,则它的高为( )
A. B. C. D.
5.菱形中,,若周长为8,则此菱形的高为( )
A.0.5 B.1 C.2 D.4
6.菱形中,对角线交于点O,给出下列结论:①,②,③,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
7.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
A.12 B.16 C.20 D.24
8.如图,菱形中,对角线相交于点O,E为边中点,菱形的周长为28,则的长等于( )
A.3.5 B.4 C.7 D.14
9.若菱形的周长为8,高为1,则菱形两邻角的度数比为( )
A.3∶1 B.4∶1 C.5∶1 D.6∶1
10.菱形中,,对角线,则菱形的边长为( )
A.2 B.4 C. D.
11.如图,在菱形中,对角线,相交于点O,下列结论中不一定成立的是( )
A. B. C. D.
12.如图,把菱形ABCD向右平移至DCEF的位置,作EG⊥AB,垂足为G,EG与CD相交于点K,GD的延长线交EF于点H,连接DE,则下列结论:①BG=AB+HF;②DG=DE;③∠DHE=∠BAD;④∠B=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.菱形是____________的平行四边形,因此它具有平行四边形的一切性质,此外菱形还具有的性质是:四条边_________,对角线_________,并且每条对角线_________.
14.菱形的判定定理包括:(1)____________的平行四边形是菱形;(2)_____________的平行四边形是菱形:(3)______________的四边形是菱形.
15.△ABC中,延长BA至D使得AB=AD,延长CA至E使得AC=AE,当△ABC满足条件________时,四边形BCDE是菱形.
16.已知菱形的两条对角线长分别为1和4,则菱形的面积为______.
17.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是_____.
18.如图,在菱形中,是对角线上的一点,于点,若,则点到的距离为________.
19.如图,平面直角坐标系中,四边形为菱形,O为坐标原点,点A坐标为,则点B的坐标是____________.
20.如图,在菱形中,对角线与相交于点O,,垂足为E点,若,则________.
三、解答题
21.如图,在菱形中,对角线与相交于点O.已知,求的长.
22.已知:如图,在菱形中,,对角线与相交于点O.
求证:(1);
(2).
23.如图,四边形是边长为的菱形,其中对角线长.求:
(1)对角线的长度;
(2)菱形的面积.
24.已知:如图,在菱形中,对角线与相交于点O,点E,F,G,H分别是,,,的中点.求证:四边形是菱形.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.D
3.B
4.D
5.B
6.C
7.D
8.A
9.C
10.B
11.B
12.C
13.有一组邻边相等 都相等 互相垂直 平分一组对角
14.有一组邻边相等 对角线互相垂直 四条边都相等
15.∠BAC=90°
16.2
17.5.
18.5
19.
20.65°
21.
解: 菱形中,对角线,相交于点,
,,
,,
,
∴的长为6cm.
22.
证明:(1)∵四边形是菱形,
∴(菱形的对边相等)
又∵,
∴.
(2)∵,
∴是等腰三角形.
又∵四边形是菱形,
∴(菱形的对角线互相平分).
在等腰三角形中,
∵,
∴,
即.
23.
解:(1)∵四边形是菱形,与相交于点E,
∴(菱形的对角线互相垂直),
(菱形的对角线互相平分).
∴.
∴(菱形的对角线互相平分);
(2)
.
24.
证明:、为、的中点,
为的中位线,
,
同理可得:,,,
又四边形为菱形,
,
,
四边形为菱形.
答案第1页,共2页
答案第1页,共2页
