人教版八年级数学下册18.2.1《矩形》随堂训练 (word版含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2.1《矩形》随堂训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 09:33:35 | ||
图片预览

文档简介
18.2.1《矩形》随堂训练
2021-2022学年人教版八年级数学下册
一、单选题
1.如图,若将矩形木框变形为平行四边形的形状,并使其面积为原矩形面积的一半,则这个平行四边形的一个最小内角的等于( )
A. B. C. D.
2.在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量四边形其中的三个角是否都为直角
3.若直角三角形两条直角边的长分别为18和24,则斜边上的中线的长是( )
A.15 B.30 C. D.
4.在矩形中,相邻两边的长分别为,则两条对角线所夹的锐角是( )
A.40° B.30° C.45° D.60°
5.如图所示,点是矩形对角线的中点,交于点,若,则的周长为( )
A.10 B. C. D.14
6.如图,四边形ABCD是平行四边形,要使它成为矩形,那么需要添加的条件是( )
A. B. C. D.
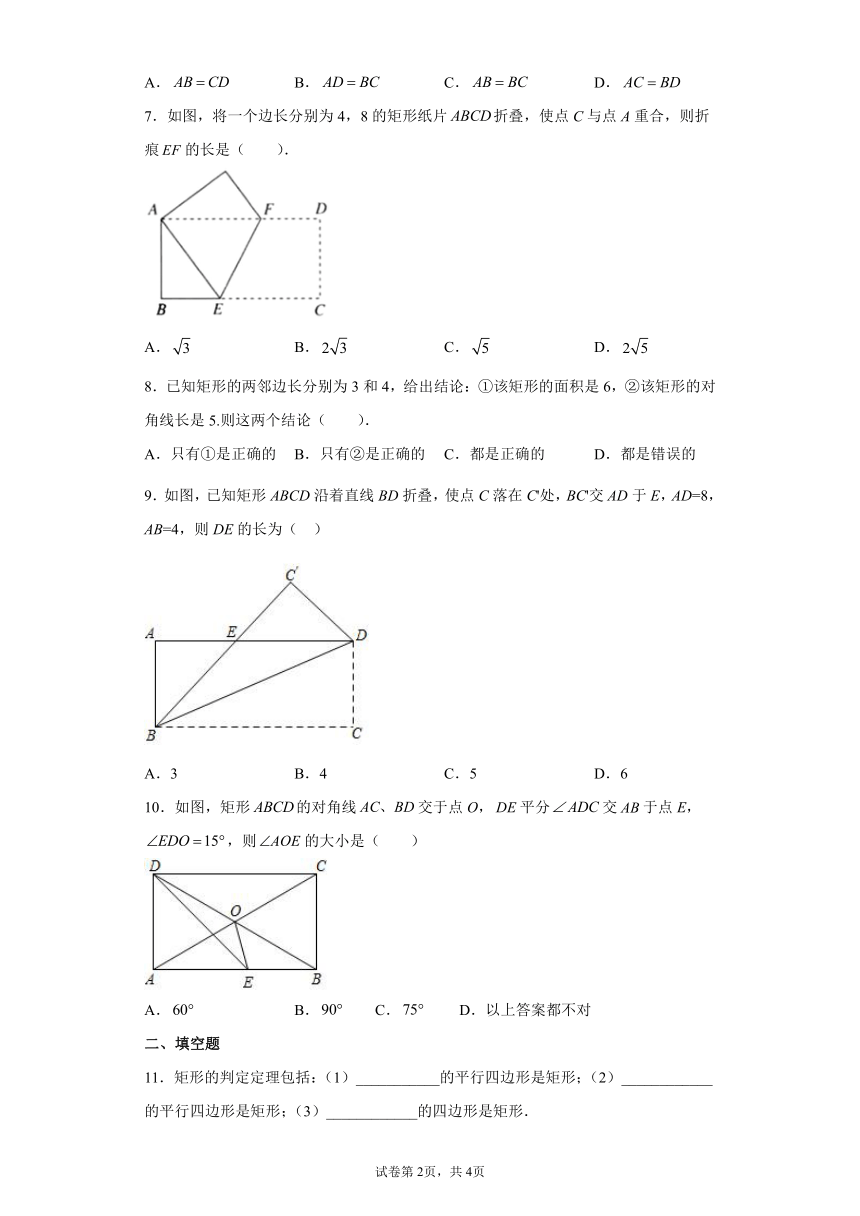
7.如图,将一个边长分别为4,8的矩形纸片折叠,使点C与点A重合,则折痕的长是( ).
A. B. C. D.
8.已知矩形的两邻边长分别为3和4,给出结论:①该矩形的面积是6,②该矩形的对角线长是5.则这两个结论( ).
A.只有①是正确的 B.只有②是正确的 C.都是正确的 D.都是错误的
9.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A.3 B.4 C.5 D.6
10.如图,矩形的对角线交于点O,平分交于点E,,则的大小是( )
A. B. C. D.以上答案都不对
二、填空题
11.矩形的判定定理包括:(1)___________的平行四边形是矩形;(2)____________的平行四边形是矩形;(3)____________的四边形是矩形.
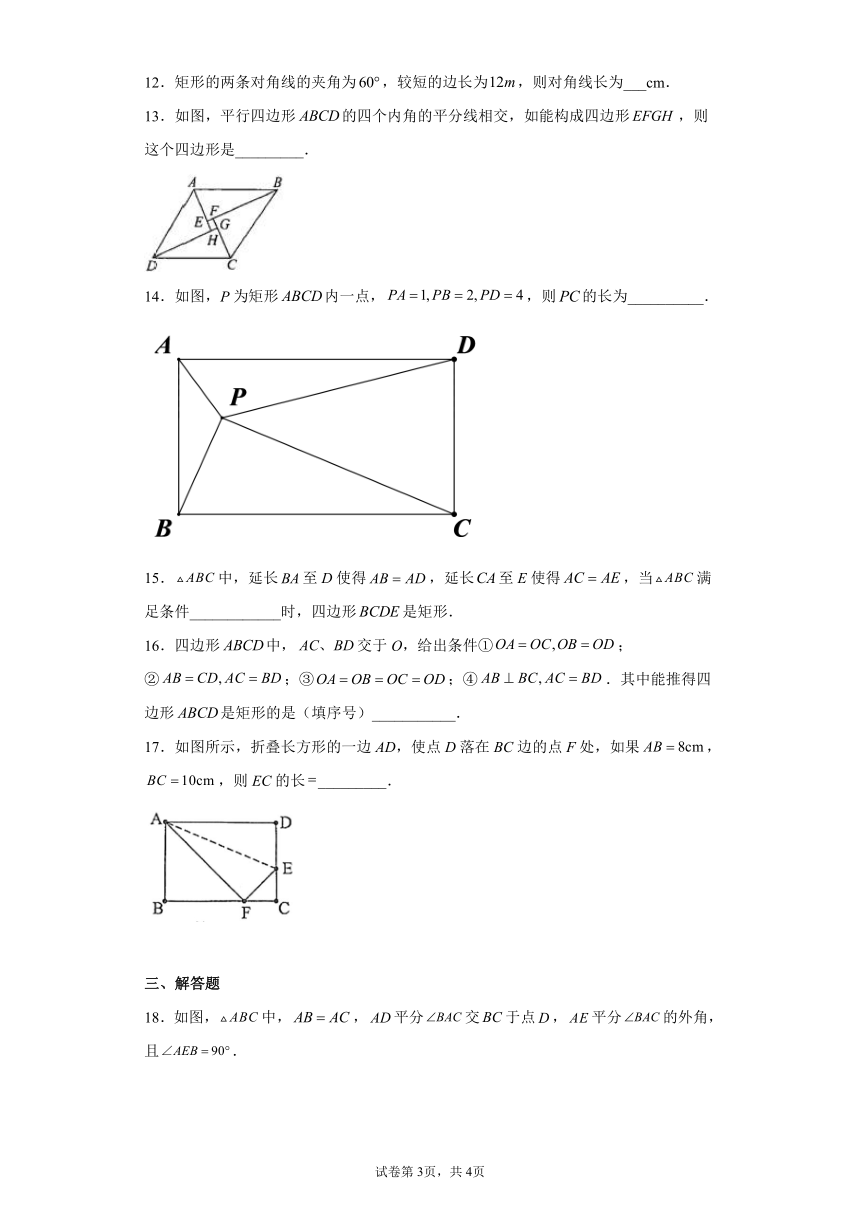
12.矩形的两条对角线的夹角为,较短的边长为,则对角线长为___cm.
13.如图,平行四边形的四个内角的平分线相交,如能构成四边形,则这个四边形是_________.
14.如图,P为矩形内一点,,则的长为__________.
15.中,延长至D使得,延长至E使得,当满足条件____________时,四边形是矩形.
16.四边形中,交于O,给出条件①;②;③;④.其中能推得四边形是矩形的是(填序号)___________.
17.如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果,,则EC的长_________.
三、解答题
18.如图,中,,平分交于点,平分的外角,且.
求证:四边形是矩形.
19.如图,在长方形中,,,求的面积和周长(结果精确到).
20.已知:如图,在矩形中,对角线与相交于点O,点M,P,N,Q分别在上,且.求证:四边形是矩形.
21.如图,在矩形中,对角线与相交于点O,过点A作的垂线,垂足为E.已知,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.D
3.A
4.D
5.C
6.D
7.D
8.B
9.C
10.C
11.有一个角是直角 对角线相等 有三个角是直角
12.
13.矩形
14.
15.
16.③
17.
18.
如图:
∵是的平分线,
∴,
∵是的平分线,
∴,
∵,
∴,
即,
∵,,
∴,
即,
∵,
∴四边形是矩形.
19.
解:∵在矩形ABCD中,BC=AD=1,∠C=∠D=90°,且∠DAE=∠CBE=45°,
∴△AED与△BCE为等腰直角三角形,
∴DE=AD=1,CE=BC=1,AE=,BE=,
∴AB=DE+CE=1+1=2,
∴△ABE的周长=AB+AE+BE=2++=2+2≈,
∴△ABE的面积=AB AD=×2×1=1.
20.
解:∵四边形ABCD是矩形,
∴∠ABC=90°;AC=BD,AO=AC,BO=BD;
∴AO=BO;而AM=BP,
∴AM:AO=BP:BO,
∴MP∥AB;
同理可证:QN∥CD;
∵AB∥CD,
∴MP∥QN;
同理可证:MQ∥PN,
∴四边形MPNQ是平行四边形;
∵MP∥AB,PN∥BC,∠ABC=90°,
∴∠MPN=90°,
∴四边形MPNQ是矩形.
21.
解:四边形是矩形,
,
,
,
∵,
,
,
四边形是矩形,
,,,
,
,
,
∴的度数为45°.
答案第1页,共2页
答案第1页,共2页
2021-2022学年人教版八年级数学下册
一、单选题
1.如图,若将矩形木框变形为平行四边形的形状,并使其面积为原矩形面积的一半,则这个平行四边形的一个最小内角的等于( )
A. B. C. D.
2.在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量四边形其中的三个角是否都为直角
3.若直角三角形两条直角边的长分别为18和24,则斜边上的中线的长是( )
A.15 B.30 C. D.
4.在矩形中,相邻两边的长分别为,则两条对角线所夹的锐角是( )
A.40° B.30° C.45° D.60°
5.如图所示,点是矩形对角线的中点,交于点,若,则的周长为( )
A.10 B. C. D.14
6.如图,四边形ABCD是平行四边形,要使它成为矩形,那么需要添加的条件是( )
A. B. C. D.
7.如图,将一个边长分别为4,8的矩形纸片折叠,使点C与点A重合,则折痕的长是( ).
A. B. C. D.
8.已知矩形的两邻边长分别为3和4,给出结论:①该矩形的面积是6,②该矩形的对角线长是5.则这两个结论( ).
A.只有①是正确的 B.只有②是正确的 C.都是正确的 D.都是错误的
9.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A.3 B.4 C.5 D.6
10.如图,矩形的对角线交于点O,平分交于点E,,则的大小是( )
A. B. C. D.以上答案都不对
二、填空题
11.矩形的判定定理包括:(1)___________的平行四边形是矩形;(2)____________的平行四边形是矩形;(3)____________的四边形是矩形.
12.矩形的两条对角线的夹角为,较短的边长为,则对角线长为___cm.
13.如图,平行四边形的四个内角的平分线相交,如能构成四边形,则这个四边形是_________.
14.如图,P为矩形内一点,,则的长为__________.
15.中,延长至D使得,延长至E使得,当满足条件____________时,四边形是矩形.
16.四边形中,交于O,给出条件①;②;③;④.其中能推得四边形是矩形的是(填序号)___________.
17.如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果,,则EC的长_________.
三、解答题
18.如图,中,,平分交于点,平分的外角,且.
求证:四边形是矩形.
19.如图,在长方形中,,,求的面积和周长(结果精确到).
20.已知:如图,在矩形中,对角线与相交于点O,点M,P,N,Q分别在上,且.求证:四边形是矩形.
21.如图,在矩形中,对角线与相交于点O,过点A作的垂线,垂足为E.已知,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.D
3.A
4.D
5.C
6.D
7.D
8.B
9.C
10.C
11.有一个角是直角 对角线相等 有三个角是直角
12.
13.矩形
14.
15.
16.③
17.
18.
如图:
∵是的平分线,
∴,
∵是的平分线,
∴,
∵,
∴,
即,
∵,,
∴,
即,
∵,
∴四边形是矩形.
19.
解:∵在矩形ABCD中,BC=AD=1,∠C=∠D=90°,且∠DAE=∠CBE=45°,
∴△AED与△BCE为等腰直角三角形,
∴DE=AD=1,CE=BC=1,AE=,BE=,
∴AB=DE+CE=1+1=2,
∴△ABE的周长=AB+AE+BE=2++=2+2≈,
∴△ABE的面积=AB AD=×2×1=1.
20.
解:∵四边形ABCD是矩形,
∴∠ABC=90°;AC=BD,AO=AC,BO=BD;
∴AO=BO;而AM=BP,
∴AM:AO=BP:BO,
∴MP∥AB;
同理可证:QN∥CD;
∵AB∥CD,
∴MP∥QN;
同理可证:MQ∥PN,
∴四边形MPNQ是平行四边形;
∵MP∥AB,PN∥BC,∠ABC=90°,
∴∠MPN=90°,
∴四边形MPNQ是矩形.
21.
解:四边形是矩形,
,
,
,
∵,
,
,
四边形是矩形,
,,,
,
,
,
∴的度数为45°.
答案第1页,共2页
答案第1页,共2页
