青岛版八年级下册9.5解直角三角形的应用
文档属性
| 名称 | 青岛版八年级下册9.5解直角三角形的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 142.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-23 22:36:26 | ||
图片预览





文档简介
课件12张PPT。解直角三角形应用举例三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系sinA=解直角三角形的依据1、3、在解直角三角形及应用时经常接触到的一些概念(2)仰角和俯角铅直线水平线视线视线仰角俯角(3)方向角如图:点A在O的北偏东30°
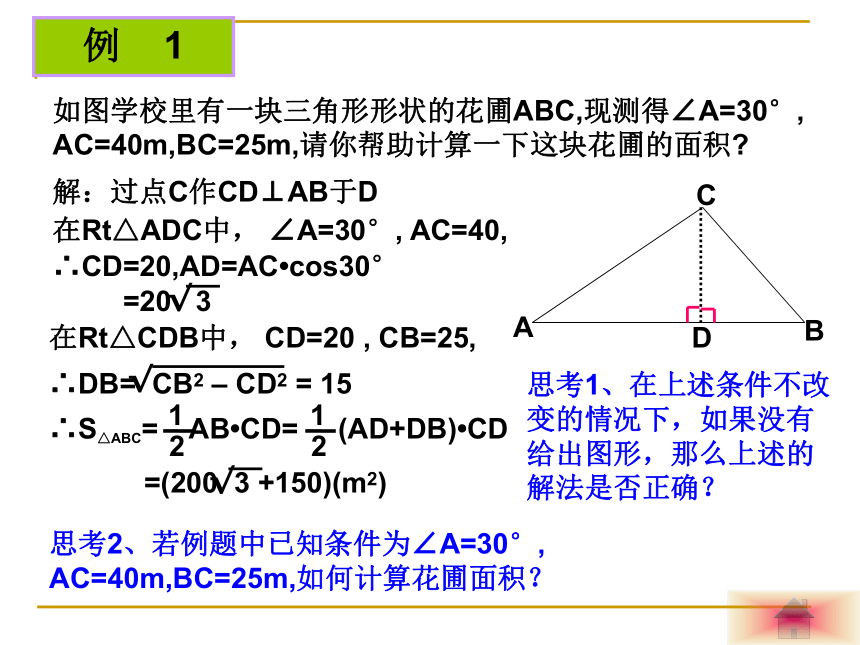
点B在点O的南偏西45°(西南方向)例 1如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20,AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,思考1、在上述条件不改变的情况下,如果没有给出图形,那么上述的解法是否正确?思考2、若例题中已知条件为∠A=30°, AC=40m,BC=25m,如何计算花圃面积?例 2 校数学兴趣小组同学打算去测量始丰溪岸一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?请帮助他们选择测量工具,并设计方案,写出必需的测量数据(用字母表示),并画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)CD=a ,BD=b方案1? ?例 2 校数学兴趣小组同学打算去测量始丰溪岸一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?请帮助他们选择测量工具,并设计方案,写出必需的测量数据(用字母表示),并画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)BD=a , ∠ACE=?(4)AB = a tg?+ 1.5方案2? ?例 3 校数学兴趣小组同学打算去测量始丰溪岸一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?若测量的铁塔位于始丰溪的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=1.5 ,DF=a方案1? ?例 3 校数学兴趣小组同学打算去测量始某铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?若测量的铁塔位于始一河流的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=b ,DF=a方案2? ?(4)1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、注意可解直角三角形与非可解直角三角形的基本解题思路;3、 现实对象 数学模型 实际问题的解 数学问题的解 数学抽象 逻辑推理 翻译回去 有无解? 作业:见 作业本 基础训练再 见
点B在点O的南偏西45°(西南方向)例 1如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20,AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,思考1、在上述条件不改变的情况下,如果没有给出图形,那么上述的解法是否正确?思考2、若例题中已知条件为∠A=30°, AC=40m,BC=25m,如何计算花圃面积?例 2 校数学兴趣小组同学打算去测量始丰溪岸一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?请帮助他们选择测量工具,并设计方案,写出必需的测量数据(用字母表示),并画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)CD=a ,BD=b方案1? ?例 2 校数学兴趣小组同学打算去测量始丰溪岸一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?请帮助他们选择测量工具,并设计方案,写出必需的测量数据(用字母表示),并画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)BD=a , ∠ACE=?(4)AB = a tg?+ 1.5方案2? ?例 3 校数学兴趣小组同学打算去测量始丰溪岸一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?若测量的铁塔位于始丰溪的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=1.5 ,DF=a方案1? ?例 3 校数学兴趣小组同学打算去测量始某铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?若测量的铁塔位于始一河流的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=b ,DF=a方案2? ?(4)1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、注意可解直角三角形与非可解直角三角形的基本解题思路;3、 现实对象 数学模型 实际问题的解 数学问题的解 数学抽象 逻辑推理 翻译回去 有无解? 作业:见 作业本 基础训练再 见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
