青岛版八年级下册9.5解直角三角形的应用

课件14张PPT。解直角三角形的应用a2+b2=c2A+B=90o解:设AB与正北方向线交于点C,则OC⊥AB。
在RTΔABC 中，
OA=500m，∠ AOC= 30o，
∴AC=OAsin ∠ AOC=500sin 30o
=500× =250（m）
OC=OAcos ∠ AOC=500 × =250 （m）
在RT ΔCOB， ∠BOC=45o，
∴BC=OC= 250 （m）
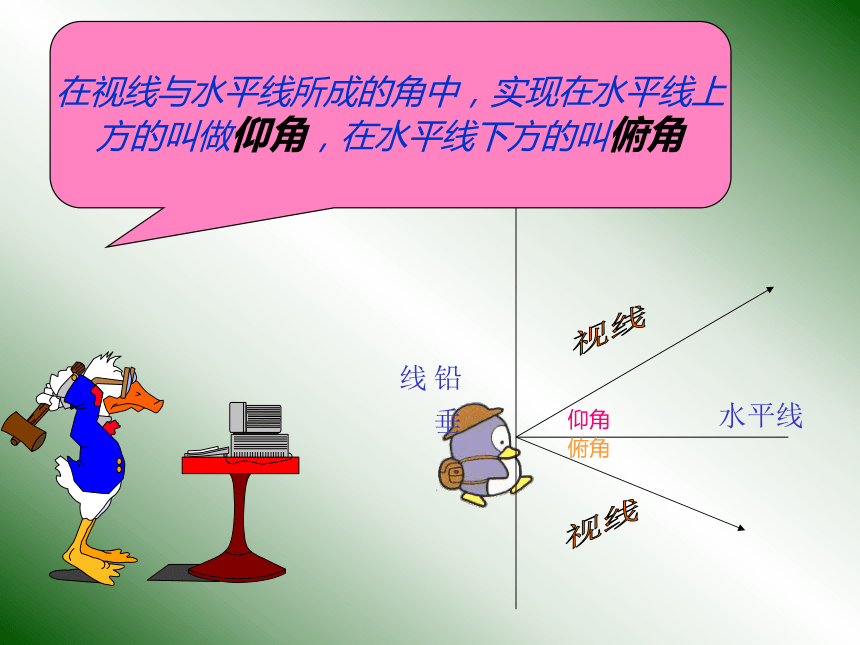
∴AB=AC+BC=250+250 （m） 在视线与水平线所成的角中，实现在水平线上
方的叫做仰角，在水平线下方的叫俯角仰角俯角例2小壁虎想到塔顶看风景,在它爬之前想知道塔有多高,已知在它爬之前它看了一下塔这时它的仰角是30°,当它向前爬行了12m时有看了一下塔,这时它的仰角是45 °.同学们你们能帮它算出塔有多高解：在RT ΔADB中，
BD=ABctg ∠ADB=Abctg45o
在RT ΔACB中，
BC=ABctg ∠ACB=ABctg30o
∵BC-BD=CD，CD=12m
∴ABctg30o－ABctg45o=12
∴AB= （m）CD怎么用含x的式子表示分析：过C作CD⊥AB于D
S ΔABC = AB ×CD (2) ∵ y=－ x2+2x=－ (x －3)2+3(0∴当x=3时,得到y最大值=3解:作CD⊥AB于D,则CD=ACsinA,
∴S ΔABC = AB ×CD ＝ AB ×ACsinA
∵ AB+AC=6cm, AC=xcm ∴AB=(6－x)cm
∵sinA= ∴y= (6－x)x×
即y=－ x2+2x,自变量x的取值范围是0tgB=2,c=2,不查表求sinB,a和
ΔABC的面积 练习思考题如图,一塔的周围有池塘,无法到达底部,但能望见底部,现在给你们卷尺和测角仪(能测量仰角,俯角和视线的夹角),利用这些现有的工具,设计一种测量铁塔高度的方案.简要说明.画出相应的图形,并简要说明计算过程