2021-2022学年湖南省张家界市永定区八年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年湖南省张家界市永定区八年级(上)期末数学试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 1017.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 12:53:40 | ||
图片预览




文档简介
2021-2022学年湖南省张家界市永定区八年级(上)期末数学试卷
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
一、选择题(本大题共8小题,共24.0分)
下列各式中,是分式的是
A. B. C. D.
已知线段,,则下列长度的线段中,能与,组成三角形的是
A. B. C. D.
成人每天维生素的摄入量约为克,将数据用科学记数法表示为
A. B. C. D.
如图,若,则添加下列一个条件后,仍无法判定≌的是
A.
B.
C.
D.
如果式子有意义,那么的取值范围在数轴上表示出来,正确的是
A. B.
C. D.
下列命题是真命题的是
A. 等腰三角形的角平分线、中线、高线互相重合
B. 一个三角形被截成两个三角形,每个三角形的内角和是度
C. 有两个角是的三角形是等边三角形
D. 在中,,则为直角三角形
关于的方程有增根,则的值是
A. B. C. D.
某商店为了促销一种定价为元的商品,采取下列方式优惠销售:若一次性购买不超过件,按原价付款;若一次性购买件以上,超过部分按原价八折付款.如果小明有元钱,那么他最多可以购买该商品
A. 件 B. 件 C. 件 D. 件
二、填空题(本大题共6小题,共18.0分)
的平方根是_____.
如图,已知≌,,,则______
一个正数的平方根分别是和,则______.
把命题“等边对等角”改写成“如果,那么”的形式是:______ .
若,则______.
在中,于点,,若,,则图中阴影部分的面积为______.
三、解答题(本大题共8小题,共58.0分)
计算:.
求不等式组的整数解.
化简式子,并在,,,,中选取一个合适的数作为的值代入求值.
已知.
求与的值;
求的算术平方根.
星期六,小明与妈妈到离家的张家界市博物馆参观.小明从家骑自行车先走,后妈妈骑摩托车从家出发,沿相同路线前往博物馆,结果他们同时到达.已知妈妈骑摩托车的平均速度是小明骑自行车平均速度的倍,求妈妈骑摩托车的平均速度.
已知:如图,中,,,,的垂直平分线交于,交于,连接.
求:的度数;
的周长.
材料:因为无理数是无限不循环小数,所以无理数的小数部分我们不可能全部写出来.比如:,等,而常用的“”或者“”的表示方法都不够百分百准确.
材料:的整数部分是,小数部分是,小数部分可以看成是得来的.
材料:任何一个无理数,都夹在两个相邻的整数之间,如,是因为.
根据上述材料,回答下列问题:
的整数部分是______,小数部分是______.
也是夹在相邻两个整数之间的,可以表示为,求的值.
已知,其中是整数,且,求的倒数.
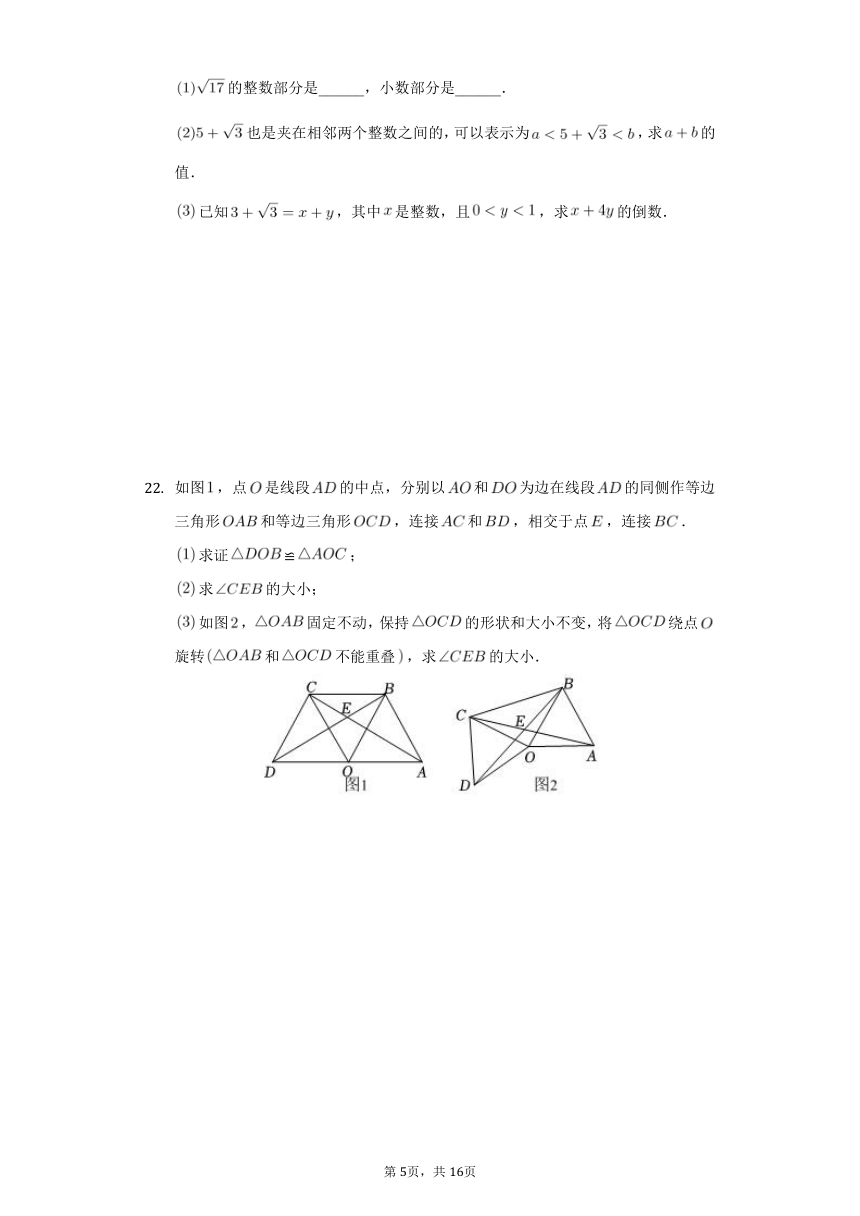
如图,点是线段的中点,分别以和为边在线段的同侧作等边三角形和等边三角形,连接和,相交于点,连接.
求证≌;
求的大小;
如图,固定不动,保持的形状和大小不变,将绕点旋转和不能重叠,求的大小.
答案和解析
1.【答案】
【解析】解:是分式,其余各选项都是整式,
故选:.
根据分式的定义即可得出答案.
本题考查了分式的定义,掌握一般地,如果,表示两个整式,并且中含有字母,那么式子叫做分式是解题的关键,注意是数字.
2.【答案】
【解析】解:,,
第三边
能与,能组成三角形的是,
故选:.
利用三角形三边关系判断即可,两边之和第三边两边之差.
考查了三角形三边关系,利用三边关系判断时,常用两个较小边的和与较大的边比较大小.两个较小边的和较大的边,则能组成三角形,否则,不可以.
3.【答案】
【解析】解:.
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
4.【答案】
【解析】解:
A、根据能推出≌,正确,本选项不符合题意;
B、根据能推出≌,正确,本选项不符合题意;
C、两边和一角对应相等的两三角形不一定全等,必须是夹角,故错误,本选项符合题意;
D、根据能推出≌,正确,本选项不符合题意;
故选:.
根据即可判断;根据即可判断;根据两三角形不一定全等即可判断;根据即可判断.
本题考查了对全等三角形的判定的应用,注意:全等三角形的一般判定方法只有,,,,共种,主要培养学生的辨析能力.
5.【答案】
【解析】解:由题意得,,
解得,,
故选:.
根据式子有意义和二次根式的概念,得到,解不等式求出解集,根据数轴上表示不等式解集的要求选出正确选项即可.
本题考查度数二次根式的概念、一元一次不等式的解法以及解集在数轴上的表示方法,正确列出不等式是解题的关键,注意在表示解集时“”,“”要用实心圆点表示;“”,“”要用空心圆点表示.
6.【答案】
【解析】解:、因为等腰三角形顶角的角平分线、底边上的中线和底边上的高线重合,故选项A错误,不符合题意;
B、因为三角形的内角和为,故选项B错误,不符合题意;
C、因为有两个角是的三角形是等边三角形,故选项C正确,符合题意;
D、,,
,
,
,
不是直角三角形,故选项D错误,不符合题意;
故选:.
A、由等腰三角形“三线合一”判定;
B、由三角形的内角和判定;
C、由等边三角形的定义判定;
D、由三角形的内角和列出方程判定的形状.
本题考查了等腰三角形的性质、三角形的内角和定理、等边三角形的定义,解题的关键是熟知等腰三角形三线合一的性质和三角形的内角和定理.
7.【答案】
【解析】解:方程两边都乘,得
,
方程有增根,
最简公分母,即增根是,
把代入整式方程,得.
故选:.
增根是分式方程化为整式方程后产生的使分式方程的分母为的根.有增根,最简公分母,所以增根是,把增根代入化为整式方程的方程即可求出未知字母的值.
本题考查了分式方程的增根,解决增根问题的步骤:
确定增根的值;化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.
8.【答案】
【解析】解:设可以购买为整数件这样的商品.
,
解得,
则最多可以购买该商品的件数是,
故选:.
购买件需要元,元超过元,则购买件数超过件,设可以购买件这样的商品,根据:件的总钱数超过件部分的总钱数,列出不等式求解即可得.
此题考查了一元一次不等式的应用,关键是读懂题意,找出题目中的数量关系,列出不等式,注意只能为整数.
9.【答案】
【解析】解:,
的平方根是.
故答案为:.
根据平方根的定义,求数的平方根,也就是求一个数,使得,则就是的平方根,由此即可解决问题.
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;的平方根是;负数没有平方根.
10.【答案】
【解析】解:≌,
,
,
,
故答案为:.
利用全等三角形的性质可得,再利用三角形内角与外角的关系可得答案.
此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
11.【答案】
【解析】解:根据题意知,
解得:,
故答案为:.
根据正数的两个平方根互为相反数列出关于的方程,解之可得.
本题主要考查的是平方根的定义和性质,熟练掌握平方根的定义和性质是解题的关键.
12.【答案】如果三角形的两条边相等,那么这两条边所对的角相等
【解析】解:“等边对等角”改写为“如果三角形的两边相等,那么这两条边所对的角相等”.
故答案为:如果三角形的两边相等,那么这两条边所对的角相等.
根据命题的定义改写即可.
本题考查了命题的定义,熟悉课本中的性质定理准确确定出题设与结论是解题的关键.
13.【答案】
【解析】解:设,
,,,
,
故答案为:.
利用设法进行计算即可.
本题考查了比例的性质,熟练掌握设法是解题的关键.
14.【答案】
【解析】解:根据题意,阴影部分的面积为三角形面积的一半,
,
阴影部分面积.
故答案为:
根据题意,观察可得:关于轴对称,且图中阴影部分的面积为面积的一半,先求出的面积,阴影部分的面积就可以得到.
考查了轴对称的性质,根据轴对称得到阴影部分面积是解题的关键.
15.【答案】解:原式
.
【解析】直接利用零指数幂的性质以及负整数指数幂的性质和有理数的乘方运算法则分别化简,进而计算得出答案.
此题主要考查了零指数幂的性质以及负整数指数幂的性质和有理数的乘方运算,正确化简各数是解题关键.
16.【答案】解:,
解不等式,得,
解不等式,得,
所以不等式组的解集为,
所以不等式组的整数解是,.
【解析】先求出每个不等式的解集,再求出不等式组的解集,最后求出不等式组的整数解即可.
本题考查了解一元一次不等式组和一元一次不等式组的整数解,能求出不等式组的解集是解此题的关键.
17.【答案】解:
,
当,,,时,原分式无意义,
当时,原式.
【解析】根据分式的加法和除法可以化简题目中的式子,然后从,,,,中选取一个使得原分式有意义的值代入化简后的式子即可解答本题.
本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
18.【答案】解:,而,,
,
解得:;
.
的平方根为,
的算术平方根为.
【解析】直接利用算术平方根以及绝对值的性质分析得出答案;
结合中所求,结合算术平方根的定义分析得出答案.
此题主要考查了算术平方根以及绝对值,正确得出,的值是解题关键.
19.【答案】解:设小明自行车的平均速度为,则妈妈骑摩托车的速度为,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
则,
答:妈妈骑摩托车的平均速度是.
【解析】设小明自行车的平均速度为,则妈妈骑摩托车的速度为,由题意:小明与妈妈到离家的张家界市博物馆参观.小明从家骑自行车先走,后妈妈骑摩托车从家出发,沿相同路线前往博物馆,结果他们同时到达.列出分式方程,解方程即可.
本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
20.【答案】解:,,
,
又为的垂直平分线,
,
,
;
已知,,
又,
,
的周长为.
【解析】首先求出,利用线段垂直平分线的性质求出,易求的度数.
已知,的长,根据线段垂直平分线的性质易求的周长.
本题考查的知识点为线段垂直平分线的性质以及等腰三角形的性质;进行角度以及线段的有效转移是正确解答本题的关键.
21.【答案】
【解析】解:,即,
的整数部分为,小数部分为,
故答案为:,;
,即,
,
又,、为相邻的整数,
,,
;
由题意可知,是的整数部分,是的小数部分,
,
,
即,
,,
,
的倒数是.
估算无理数的大小,即可确定它的整数部分、小数部分,进而得出答案;
估算无理数的大小,进而得出的大小,确定、的值,再代入计算即可;
根据题意,估算无理数的大小,确定它的整数部分和小数部分,得出、的值,代入计算即可.
本题考查估算无理数的大小,掌握算术平方根的定义是正确解答的前提,确定无理数的整数部分和小数部分是解决问题的关键.
22.【答案】证明:如图,
和都是等边三角形,
,,
,
在和中
≌;
解:如图,
和都是等边三角形,
且点是线段的中点,
,,
.
又,
.
同理.
,
,
;
解:如图,
和都是等边三角形,
,,.
,,
,.
,,
.
,,
,
.
又,,
,
,
.
【解析】如图,根据等边三角形的性质得到,,则利用根据“”判断≌;
利用≌得到,然后根据三角形内角和可得到;
如图,与的方法一样可证明≌;则,然后根据三角形内角和可求出,进而解答即可.
本题考查了几何变换综合题:熟练掌握旋转的性质、等边三角形的性质和全等三角形的判定与性质;利用类比的方法解决小题.
第2页,共2页
第1页,共1页
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
一、选择题(本大题共8小题,共24.0分)
下列各式中,是分式的是
A. B. C. D.
已知线段,,则下列长度的线段中,能与,组成三角形的是
A. B. C. D.
成人每天维生素的摄入量约为克,将数据用科学记数法表示为
A. B. C. D.
如图,若,则添加下列一个条件后,仍无法判定≌的是
A.
B.
C.
D.
如果式子有意义,那么的取值范围在数轴上表示出来,正确的是
A. B.
C. D.
下列命题是真命题的是
A. 等腰三角形的角平分线、中线、高线互相重合
B. 一个三角形被截成两个三角形,每个三角形的内角和是度
C. 有两个角是的三角形是等边三角形
D. 在中,,则为直角三角形
关于的方程有增根,则的值是
A. B. C. D.
某商店为了促销一种定价为元的商品,采取下列方式优惠销售:若一次性购买不超过件,按原价付款;若一次性购买件以上,超过部分按原价八折付款.如果小明有元钱,那么他最多可以购买该商品
A. 件 B. 件 C. 件 D. 件
二、填空题(本大题共6小题,共18.0分)
的平方根是_____.
如图,已知≌,,,则______
一个正数的平方根分别是和,则______.
把命题“等边对等角”改写成“如果,那么”的形式是:______ .
若,则______.
在中,于点,,若,,则图中阴影部分的面积为______.
三、解答题(本大题共8小题,共58.0分)
计算:.
求不等式组的整数解.
化简式子,并在,,,,中选取一个合适的数作为的值代入求值.
已知.
求与的值;
求的算术平方根.
星期六,小明与妈妈到离家的张家界市博物馆参观.小明从家骑自行车先走,后妈妈骑摩托车从家出发,沿相同路线前往博物馆,结果他们同时到达.已知妈妈骑摩托车的平均速度是小明骑自行车平均速度的倍,求妈妈骑摩托车的平均速度.
已知:如图,中,,,,的垂直平分线交于,交于,连接.
求:的度数;
的周长.
材料:因为无理数是无限不循环小数,所以无理数的小数部分我们不可能全部写出来.比如:,等,而常用的“”或者“”的表示方法都不够百分百准确.
材料:的整数部分是,小数部分是,小数部分可以看成是得来的.
材料:任何一个无理数,都夹在两个相邻的整数之间,如,是因为.
根据上述材料,回答下列问题:
的整数部分是______,小数部分是______.
也是夹在相邻两个整数之间的,可以表示为,求的值.
已知,其中是整数,且,求的倒数.
如图,点是线段的中点,分别以和为边在线段的同侧作等边三角形和等边三角形,连接和,相交于点,连接.
求证≌;
求的大小;
如图,固定不动,保持的形状和大小不变,将绕点旋转和不能重叠,求的大小.
答案和解析
1.【答案】
【解析】解:是分式,其余各选项都是整式,
故选:.
根据分式的定义即可得出答案.
本题考查了分式的定义,掌握一般地,如果,表示两个整式,并且中含有字母,那么式子叫做分式是解题的关键,注意是数字.
2.【答案】
【解析】解:,,
第三边
能与,能组成三角形的是,
故选:.
利用三角形三边关系判断即可,两边之和第三边两边之差.
考查了三角形三边关系,利用三边关系判断时,常用两个较小边的和与较大的边比较大小.两个较小边的和较大的边,则能组成三角形,否则,不可以.
3.【答案】
【解析】解:.
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
4.【答案】
【解析】解:
A、根据能推出≌,正确,本选项不符合题意;
B、根据能推出≌,正确,本选项不符合题意;
C、两边和一角对应相等的两三角形不一定全等,必须是夹角,故错误,本选项符合题意;
D、根据能推出≌,正确,本选项不符合题意;
故选:.
根据即可判断;根据即可判断;根据两三角形不一定全等即可判断;根据即可判断.
本题考查了对全等三角形的判定的应用,注意:全等三角形的一般判定方法只有,,,,共种,主要培养学生的辨析能力.
5.【答案】
【解析】解:由题意得,,
解得,,
故选:.
根据式子有意义和二次根式的概念,得到,解不等式求出解集,根据数轴上表示不等式解集的要求选出正确选项即可.
本题考查度数二次根式的概念、一元一次不等式的解法以及解集在数轴上的表示方法,正确列出不等式是解题的关键,注意在表示解集时“”,“”要用实心圆点表示;“”,“”要用空心圆点表示.
6.【答案】
【解析】解:、因为等腰三角形顶角的角平分线、底边上的中线和底边上的高线重合,故选项A错误,不符合题意;
B、因为三角形的内角和为,故选项B错误,不符合题意;
C、因为有两个角是的三角形是等边三角形,故选项C正确,符合题意;
D、,,
,
,
,
不是直角三角形,故选项D错误,不符合题意;
故选:.
A、由等腰三角形“三线合一”判定;
B、由三角形的内角和判定;
C、由等边三角形的定义判定;
D、由三角形的内角和列出方程判定的形状.
本题考查了等腰三角形的性质、三角形的内角和定理、等边三角形的定义,解题的关键是熟知等腰三角形三线合一的性质和三角形的内角和定理.
7.【答案】
【解析】解:方程两边都乘,得
,
方程有增根,
最简公分母,即增根是,
把代入整式方程,得.
故选:.
增根是分式方程化为整式方程后产生的使分式方程的分母为的根.有增根,最简公分母,所以增根是,把增根代入化为整式方程的方程即可求出未知字母的值.
本题考查了分式方程的增根,解决增根问题的步骤:
确定增根的值;化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.
8.【答案】
【解析】解:设可以购买为整数件这样的商品.
,
解得,
则最多可以购买该商品的件数是,
故选:.
购买件需要元,元超过元,则购买件数超过件,设可以购买件这样的商品,根据:件的总钱数超过件部分的总钱数,列出不等式求解即可得.
此题考查了一元一次不等式的应用,关键是读懂题意,找出题目中的数量关系,列出不等式,注意只能为整数.
9.【答案】
【解析】解:,
的平方根是.
故答案为:.
根据平方根的定义,求数的平方根,也就是求一个数,使得,则就是的平方根,由此即可解决问题.
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;的平方根是;负数没有平方根.
10.【答案】
【解析】解:≌,
,
,
,
故答案为:.
利用全等三角形的性质可得,再利用三角形内角与外角的关系可得答案.
此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
11.【答案】
【解析】解:根据题意知,
解得:,
故答案为:.
根据正数的两个平方根互为相反数列出关于的方程,解之可得.
本题主要考查的是平方根的定义和性质,熟练掌握平方根的定义和性质是解题的关键.
12.【答案】如果三角形的两条边相等,那么这两条边所对的角相等
【解析】解:“等边对等角”改写为“如果三角形的两边相等,那么这两条边所对的角相等”.
故答案为:如果三角形的两边相等,那么这两条边所对的角相等.
根据命题的定义改写即可.
本题考查了命题的定义,熟悉课本中的性质定理准确确定出题设与结论是解题的关键.
13.【答案】
【解析】解:设,
,,,
,
故答案为:.
利用设法进行计算即可.
本题考查了比例的性质,熟练掌握设法是解题的关键.
14.【答案】
【解析】解:根据题意,阴影部分的面积为三角形面积的一半,
,
阴影部分面积.
故答案为:
根据题意,观察可得:关于轴对称,且图中阴影部分的面积为面积的一半,先求出的面积,阴影部分的面积就可以得到.
考查了轴对称的性质,根据轴对称得到阴影部分面积是解题的关键.
15.【答案】解:原式
.
【解析】直接利用零指数幂的性质以及负整数指数幂的性质和有理数的乘方运算法则分别化简,进而计算得出答案.
此题主要考查了零指数幂的性质以及负整数指数幂的性质和有理数的乘方运算,正确化简各数是解题关键.
16.【答案】解:,
解不等式,得,
解不等式,得,
所以不等式组的解集为,
所以不等式组的整数解是,.
【解析】先求出每个不等式的解集,再求出不等式组的解集,最后求出不等式组的整数解即可.
本题考查了解一元一次不等式组和一元一次不等式组的整数解,能求出不等式组的解集是解此题的关键.
17.【答案】解:
,
当,,,时,原分式无意义,
当时,原式.
【解析】根据分式的加法和除法可以化简题目中的式子,然后从,,,,中选取一个使得原分式有意义的值代入化简后的式子即可解答本题.
本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
18.【答案】解:,而,,
,
解得:;
.
的平方根为,
的算术平方根为.
【解析】直接利用算术平方根以及绝对值的性质分析得出答案;
结合中所求,结合算术平方根的定义分析得出答案.
此题主要考查了算术平方根以及绝对值,正确得出,的值是解题关键.
19.【答案】解:设小明自行车的平均速度为,则妈妈骑摩托车的速度为,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
则,
答:妈妈骑摩托车的平均速度是.
【解析】设小明自行车的平均速度为,则妈妈骑摩托车的速度为,由题意:小明与妈妈到离家的张家界市博物馆参观.小明从家骑自行车先走,后妈妈骑摩托车从家出发,沿相同路线前往博物馆,结果他们同时到达.列出分式方程,解方程即可.
本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
20.【答案】解:,,
,
又为的垂直平分线,
,
,
;
已知,,
又,
,
的周长为.
【解析】首先求出,利用线段垂直平分线的性质求出,易求的度数.
已知,的长,根据线段垂直平分线的性质易求的周长.
本题考查的知识点为线段垂直平分线的性质以及等腰三角形的性质;进行角度以及线段的有效转移是正确解答本题的关键.
21.【答案】
【解析】解:,即,
的整数部分为,小数部分为,
故答案为:,;
,即,
,
又,、为相邻的整数,
,,
;
由题意可知,是的整数部分,是的小数部分,
,
,
即,
,,
,
的倒数是.
估算无理数的大小,即可确定它的整数部分、小数部分,进而得出答案;
估算无理数的大小,进而得出的大小,确定、的值,再代入计算即可;
根据题意,估算无理数的大小,确定它的整数部分和小数部分,得出、的值,代入计算即可.
本题考查估算无理数的大小,掌握算术平方根的定义是正确解答的前提,确定无理数的整数部分和小数部分是解决问题的关键.
22.【答案】证明:如图,
和都是等边三角形,
,,
,
在和中
≌;
解:如图,
和都是等边三角形,
且点是线段的中点,
,,
.
又,
.
同理.
,
,
;
解:如图,
和都是等边三角形,
,,.
,,
,.
,,
.
,,
,
.
又,,
,
,
.
【解析】如图,根据等边三角形的性质得到,,则利用根据“”判断≌;
利用≌得到,然后根据三角形内角和可得到;
如图,与的方法一样可证明≌;则,然后根据三角形内角和可求出,进而解答即可.
本题考查了几何变换综合题:熟练掌握旋转的性质、等边三角形的性质和全等三角形的判定与性质;利用类比的方法解决小题.
第2页,共2页
第1页,共1页
同课章节目录
