2021——2022学年度人教版八年级数学下册 17.1 勾股定理课后练习(Word版含答案)
文档属性
| 名称 | 2021——2022学年度人教版八年级数学下册 17.1 勾股定理课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 409.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 19:47:37 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学下册 第十七章 勾股定理 17.1 勾股定理课后练习
一、选择题
1.下列各组数是勾股数的是( )
A.1,2,3 B.3,4,5 C.4,5,6 D.6,7,8
2.在平面直角坐标系中,为坐标原点,点,点,,且满足.若的面积为,则的值不可能为( )
A.18 B.46 C.82 D.55
3.中,有一点在上移动.若,,的最小值为( )
A.10 B.9.8 C.8.8 D.4.8
4.如图,四边形是边长为9的正方形纸片,将其沿折叠,使点落在边上的点处,点的对应点为点,,则的长为( )
A.1.8 B.2 C.2.3 D.
5.在中,,,,三个内角的平分线交于点,则点到的距离为( )
A.1cm B.2cm C.cm D.cm
6.如图,由四个全等的直角三角形拼成的图形,设CE=a,HG=b,则斜边BD的长是( )
A.a+b B.a﹣b C. D.
7.如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方形盒子的外表面从点爬行到点,它需要爬行的最短路程为( )
A. B. C. D.
8.如图,在数轴上,点O对应数字O,点A对应数字2,过点A作AB垂直于数轴,且AB=4,连接OB,绕点O顺时针旋转OB,使点B落在数轴上的点C处,则点C所表示的数介于( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
9.如图,在长方体盒子上有一只蚂蚁从顶点出发,要爬行到顶点去找食物,已知长方体的长、宽、高分别为4、1、2,则蚂蚁走的最短路径长为( )
A. B.5 C. D.7
10.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10 B.7 C.6 D.12
二、填空题
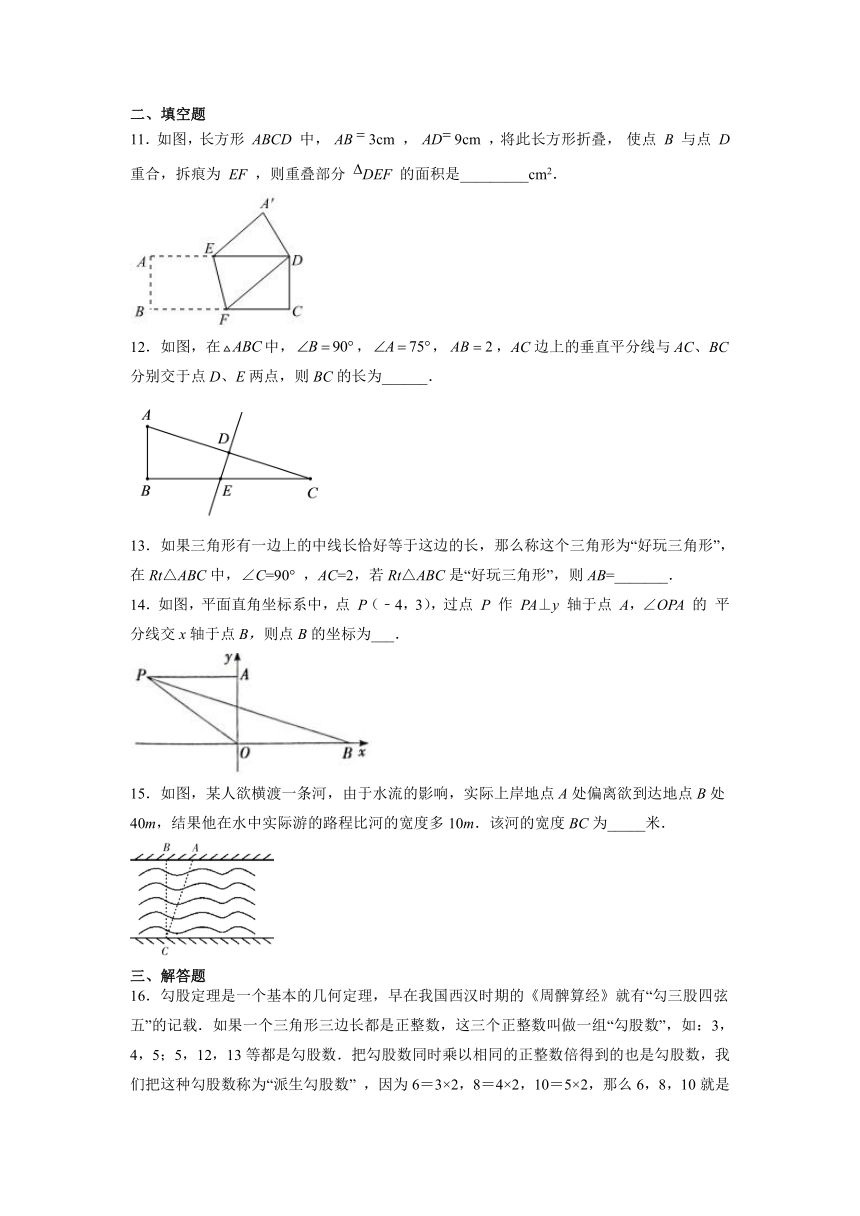
11.如图,长方形 ABCD 中, AB 3cm , AD 9cm ,将此长方形折叠, 使点 B 与点 D 重合,拆痕为 EF ,则重叠部分 DEF 的面积是_________cm2.
12.如图,在中,,,,AC边上的垂直平分线与AC、BC分别交于点D、E两点,则BC的长为______.
13.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90° ,AC=2,若Rt△ABC是“好玩三角形”,则AB=_______.
14.如图,平面直角坐标系中,点 P(﹣4,3),过点 P 作 PA⊥y 轴于点 A,∠OPA 的 平分线交x轴于点B,则点B的坐标为___.
15.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点A处偏离欲到达地点B处40m,结果他在水中实际游的路程比河的宽度多10m.该河的宽度BC为_____米.
三、解答题
16.勾股定理是一个基本的几何定理,早在我国西汉时期的《周髀算经》就有“勾三股四弦五”的记载.如果一个三角形三边长都是正整数,这三个正整数叫做一组“勾股数”,如:3,4,5;5,12,13等都是勾股数.把勾股数同时乘以相同的正整数倍得到的也是勾股数,我们把这种勾股数称为“派生勾股数” ,因为6=3×2,8=4×2,10=5×2,那么6,8,10就是“派生勾股数”,如果一组勾股数斜边比一条直角边大3,我们把这种勾股数称为“新新勾股数”.
(1)请判断9,12,16和10,24,26是否为“派生勾股数”;
(2)请求出斜边小于200的所有“新新勾股数”.
17.如图,平面直角坐标系中,已知点,点,连接则可量出.若对于平面内一点C,当是以为腰的等腰三角形时,称点C是线段的“等长点”.
(1)在点,点,点中,线段的“等长点”是点 ;
(2)若点是线段的“等长点”,且,求m和n的值.
18.数学中,常对同一个量(图形的面积、点的个数等)用两种不同的方法计算,从而建立相等关系,我们把这种思想叫“算两次”.“算两次”也称作富比尼原理,是一种重要的数学思想,由它可以推导出很多重要的公式.
(1)如图1,是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形.
①用“算两次”的方法计算图2中阴影部分的面积:第一次列式为 ,第二次列式为 ,因为两次所列算式表示的是同一个图形的面积,所以可以得出等式 ;
②在①中,如果,,请直接用①题中的等式,求阴影部分的面积;
(2)如图3,两个边长分别为,,的直角三角形和一个两条直角边都是的直角三角形拼成一个梯形,用“算两次”的方法,探究,,之间的数量关系.
19.将一个正方形纸片如图1所示摆放在平面直角坐标系中,使正方形纸片的四个顶点恰好都落在坐标轴上,其中落在轴正半轴上的顶点坐标为,经探究可以发现,若把正方形纸片沿轴和轴剪开,可拼成如图2所示的两个小正方形.
(1)当时,正方形的边长是__________.
(2)当时,是否能用正方形纸片,沿着边的方向裁出一个面积为的长方形,使它的长与宽的比是?如果能,求出长方形的长和宽;如果不能,请说明理由.
20.已知:在平面直角坐标系中,点O为坐标原点,和关于y轴对称,且,
(1)如图1,求的度数;
(2)如图2,点P为线段延长线上一点,交x轴于点D,设,点P的横坐标为d,求d与t之间的数量关系;
(3)如图3,在(2)的条件下,点E为x轴上一点,连接交y轴于点F,且,,在的延长线上取一点Q,使,求点Q的横坐标.
21.如图,射线于点、点、在、上,为线段的中点,且于点.
(1)若,直接写出的值;
(2)若,的周长为24,求的面积;
(3)若,点在射线上移动,问此过程中,的值是否为定值?若是,请求出这个定值;若不是,请求出它的取值范围.
22.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
23.如图,一个长方体形盒子的长、宽、高分别为4cm,4cm,6cm
(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,请你帮蚂蚁设计一条最短的路线,蚂蚁要爬行的最短路线是多少?
(2)若将一根木棒放进盒子里并能盖上盖子,则能放入该盒子里的木棒的最大长度是多少cm (结果可保留根号)
【参考答案】
1.B 2.D 3.A 4.B 5.B 6.C 7.A 8.C 9.B 10.B
11.7.5
12.
13.或
14.(5,0)
15.75
16.(1)9,12,16不是“派生勾股数”; 10,24,26是“派生勾股数”;(2)15、36、39;15、36、39;21、72、75;27、120、123;22、180、183
17.(1)C1和C2;(2),或,.
18.(1)①,,;或,,;②9;(2)
19.(1);(2)不能.
20.(1)22.5°;(2)d=2t;(3)5
21.(1);(2);(3)是定值,值是
22.
23.(1)10cm;(2)cm
一、选择题
1.下列各组数是勾股数的是( )
A.1,2,3 B.3,4,5 C.4,5,6 D.6,7,8
2.在平面直角坐标系中,为坐标原点,点,点,,且满足.若的面积为,则的值不可能为( )
A.18 B.46 C.82 D.55
3.中,有一点在上移动.若,,的最小值为( )
A.10 B.9.8 C.8.8 D.4.8
4.如图,四边形是边长为9的正方形纸片,将其沿折叠,使点落在边上的点处,点的对应点为点,,则的长为( )
A.1.8 B.2 C.2.3 D.
5.在中,,,,三个内角的平分线交于点,则点到的距离为( )
A.1cm B.2cm C.cm D.cm
6.如图,由四个全等的直角三角形拼成的图形,设CE=a,HG=b,则斜边BD的长是( )
A.a+b B.a﹣b C. D.
7.如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方形盒子的外表面从点爬行到点,它需要爬行的最短路程为( )
A. B. C. D.
8.如图,在数轴上,点O对应数字O,点A对应数字2,过点A作AB垂直于数轴,且AB=4,连接OB,绕点O顺时针旋转OB,使点B落在数轴上的点C处,则点C所表示的数介于( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
9.如图,在长方体盒子上有一只蚂蚁从顶点出发,要爬行到顶点去找食物,已知长方体的长、宽、高分别为4、1、2,则蚂蚁走的最短路径长为( )
A. B.5 C. D.7
10.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10 B.7 C.6 D.12
二、填空题
11.如图,长方形 ABCD 中, AB 3cm , AD 9cm ,将此长方形折叠, 使点 B 与点 D 重合,拆痕为 EF ,则重叠部分 DEF 的面积是_________cm2.
12.如图,在中,,,,AC边上的垂直平分线与AC、BC分别交于点D、E两点,则BC的长为______.
13.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90° ,AC=2,若Rt△ABC是“好玩三角形”,则AB=_______.
14.如图,平面直角坐标系中,点 P(﹣4,3),过点 P 作 PA⊥y 轴于点 A,∠OPA 的 平分线交x轴于点B,则点B的坐标为___.
15.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点A处偏离欲到达地点B处40m,结果他在水中实际游的路程比河的宽度多10m.该河的宽度BC为_____米.
三、解答题
16.勾股定理是一个基本的几何定理,早在我国西汉时期的《周髀算经》就有“勾三股四弦五”的记载.如果一个三角形三边长都是正整数,这三个正整数叫做一组“勾股数”,如:3,4,5;5,12,13等都是勾股数.把勾股数同时乘以相同的正整数倍得到的也是勾股数,我们把这种勾股数称为“派生勾股数” ,因为6=3×2,8=4×2,10=5×2,那么6,8,10就是“派生勾股数”,如果一组勾股数斜边比一条直角边大3,我们把这种勾股数称为“新新勾股数”.
(1)请判断9,12,16和10,24,26是否为“派生勾股数”;
(2)请求出斜边小于200的所有“新新勾股数”.
17.如图,平面直角坐标系中,已知点,点,连接则可量出.若对于平面内一点C,当是以为腰的等腰三角形时,称点C是线段的“等长点”.
(1)在点,点,点中,线段的“等长点”是点 ;
(2)若点是线段的“等长点”,且,求m和n的值.
18.数学中,常对同一个量(图形的面积、点的个数等)用两种不同的方法计算,从而建立相等关系,我们把这种思想叫“算两次”.“算两次”也称作富比尼原理,是一种重要的数学思想,由它可以推导出很多重要的公式.
(1)如图1,是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形.
①用“算两次”的方法计算图2中阴影部分的面积:第一次列式为 ,第二次列式为 ,因为两次所列算式表示的是同一个图形的面积,所以可以得出等式 ;
②在①中,如果,,请直接用①题中的等式,求阴影部分的面积;
(2)如图3,两个边长分别为,,的直角三角形和一个两条直角边都是的直角三角形拼成一个梯形,用“算两次”的方法,探究,,之间的数量关系.
19.将一个正方形纸片如图1所示摆放在平面直角坐标系中,使正方形纸片的四个顶点恰好都落在坐标轴上,其中落在轴正半轴上的顶点坐标为,经探究可以发现,若把正方形纸片沿轴和轴剪开,可拼成如图2所示的两个小正方形.
(1)当时,正方形的边长是__________.
(2)当时,是否能用正方形纸片,沿着边的方向裁出一个面积为的长方形,使它的长与宽的比是?如果能,求出长方形的长和宽;如果不能,请说明理由.
20.已知:在平面直角坐标系中,点O为坐标原点,和关于y轴对称,且,
(1)如图1,求的度数;
(2)如图2,点P为线段延长线上一点,交x轴于点D,设,点P的横坐标为d,求d与t之间的数量关系;
(3)如图3,在(2)的条件下,点E为x轴上一点,连接交y轴于点F,且,,在的延长线上取一点Q,使,求点Q的横坐标.
21.如图,射线于点、点、在、上,为线段的中点,且于点.
(1)若,直接写出的值;
(2)若,的周长为24,求的面积;
(3)若,点在射线上移动,问此过程中,的值是否为定值?若是,请求出这个定值;若不是,请求出它的取值范围.
22.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
23.如图,一个长方体形盒子的长、宽、高分别为4cm,4cm,6cm
(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,请你帮蚂蚁设计一条最短的路线,蚂蚁要爬行的最短路线是多少?
(2)若将一根木棒放进盒子里并能盖上盖子,则能放入该盒子里的木棒的最大长度是多少cm (结果可保留根号)
【参考答案】
1.B 2.D 3.A 4.B 5.B 6.C 7.A 8.C 9.B 10.B
11.7.5
12.
13.或
14.(5,0)
15.75
16.(1)9,12,16不是“派生勾股数”; 10,24,26是“派生勾股数”;(2)15、36、39;15、36、39;21、72、75;27、120、123;22、180、183
17.(1)C1和C2;(2),或,.
18.(1)①,,;或,,;②9;(2)
19.(1);(2)不能.
20.(1)22.5°;(2)d=2t;(3)5
21.(1);(2);(3)是定值,值是
22.
23.(1)10cm;(2)cm
