2021-2022学年人教版七年级数学下册5.2.2平行线的判定基础练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.2平行线的判定基础练习 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 325.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 08:45:09 | ||
图片预览

文档简介
5.2.2平行线的判定提高练习
2021--2022学年人教版七年级数学下册
一、单选题
1.如图,工人师傅用角尺画出工件边缘的垂线和,得到,理由是( )
A.在同一平面内,垂直于同一条直线的两条直线平行
B.在同一平面内,过一点有且仅有一条直线垂直于已知直线
C.连接直线外一点与直线各点的所有直线中,垂线段最短
D.经过直线外一点,有且只有一条直线与这条直线平行
2.已知,,是三条直线,下列结论正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
3.用反证法证明命题“在同一平面内,若 ,则 a∥c”时,首先应假设( )
A.a∥b B.b∥c C.a 与 c 相交 D.a 与 b
4.如图,现给出下列条件:① ,② ,③ ,④,⑤ .其中能够得到ABCD的条件的个数( )
A.2个 B.3个 C.4个 D.5个
5.如图所示,下列条件中,不能推出AB∥CE成立的条件是( )
A.∠A=∠ACE B.∠B=∠ACE C.∠B=∠ECD D.∠B+∠BCE=180°
6.如图,下列条件能判断直线l1//l2的有( )
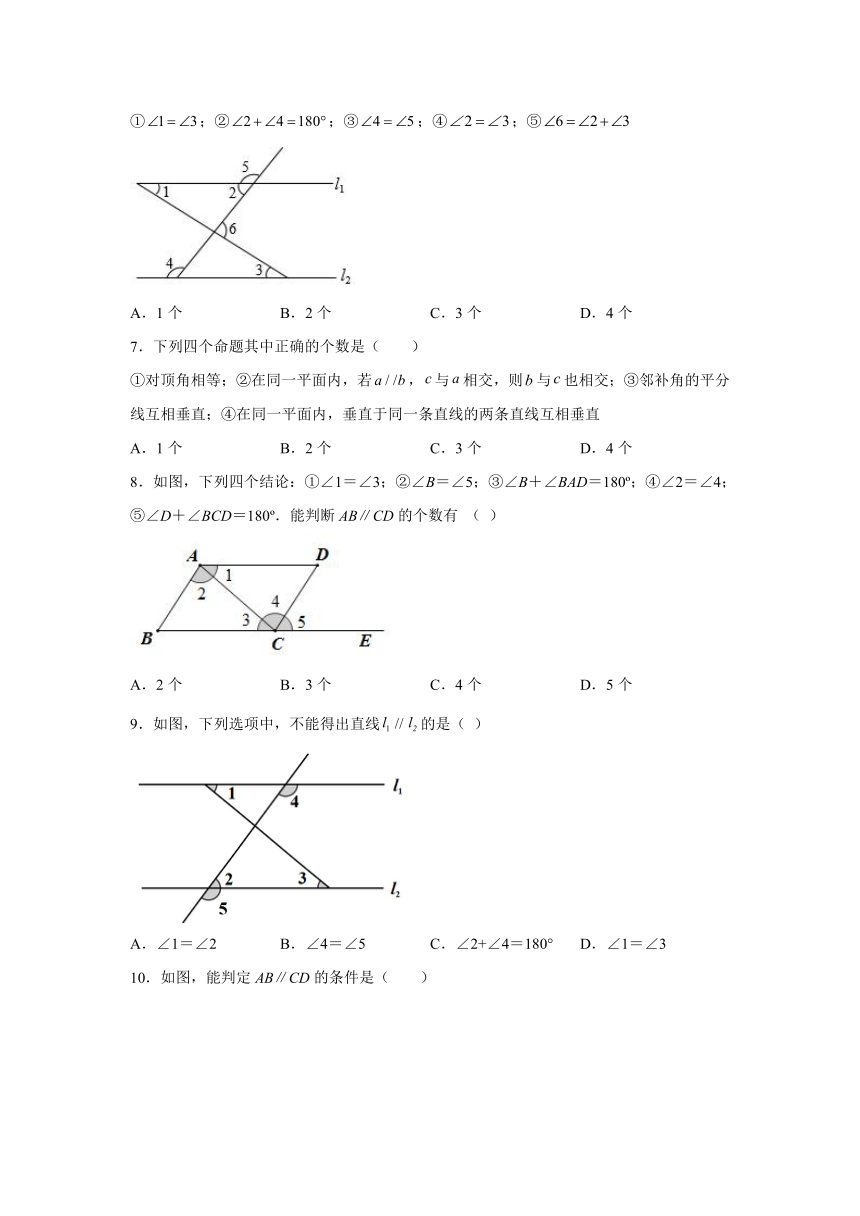
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
7.下列四个命题其中正确的个数是( )
①对顶角相等;②在同一平面内,若,与相交,则与也相交;③邻补角的平分线互相垂直;④在同一平面内,垂直于同一条直线的两条直线互相垂直
A.1个 B.2个 C.3个 D.4个
8.如图,下列四个结论:①∠1=∠3;②∠B=∠5;③∠B+∠BAD=180 ;④∠2=∠4;⑤∠D+∠BCD=180 .能判断AB∥CD的个数有 ( )
A.2个 B.3个 C.4个 D.5个
9.如图,下列选项中,不能得出直线的是( )
A.∠1=∠2 B.∠4=∠5 C.∠2+∠4=180° D.∠1=∠3
10.如图,能判定AB∥CD的条件是( )
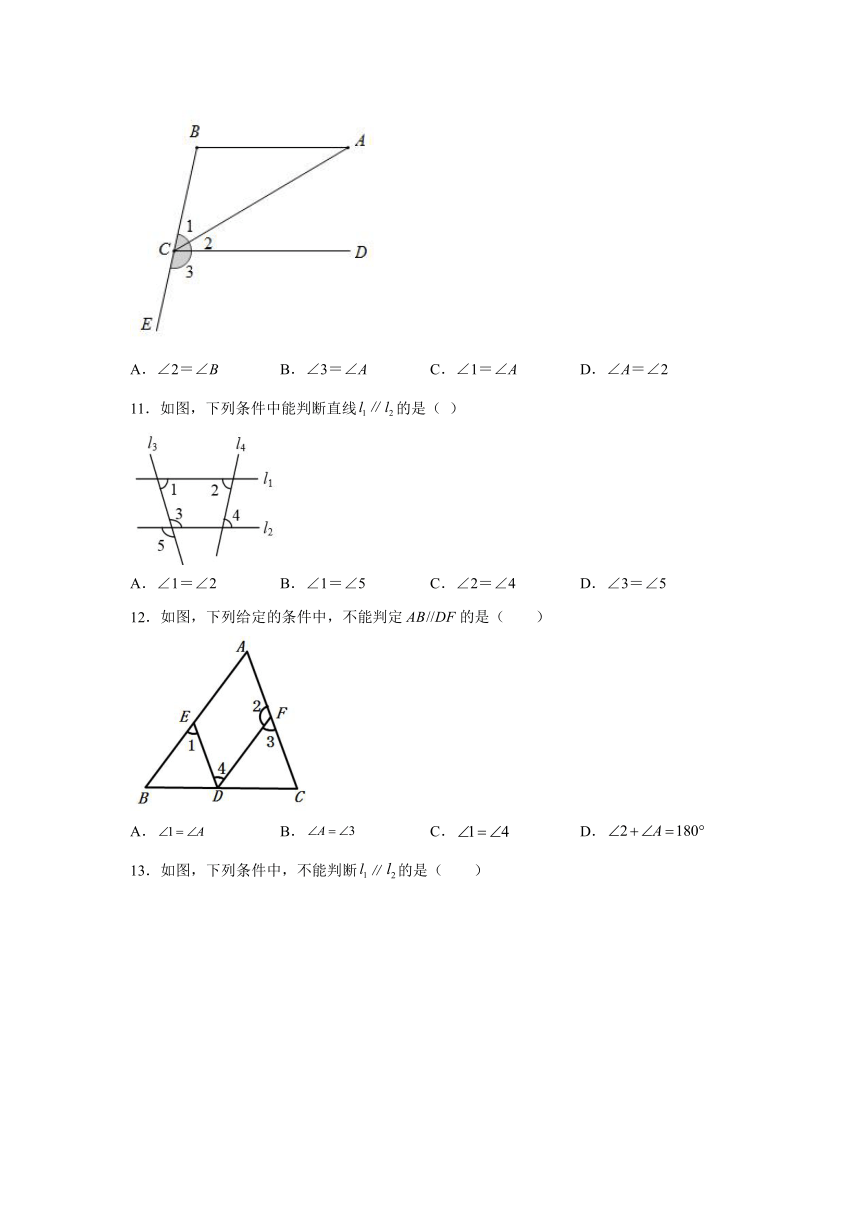
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
11.如图,下列条件中能判断直线的是( )
A.∠1=∠2 B.∠1=∠5 C.∠2=∠4 D.∠3=∠5
12.如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
13.如图,下列条件中,不能判断∥的是( )
A.∠1=∠3 B.∠2=∠4 C.∠4+∠5=180° D.∠3=∠4
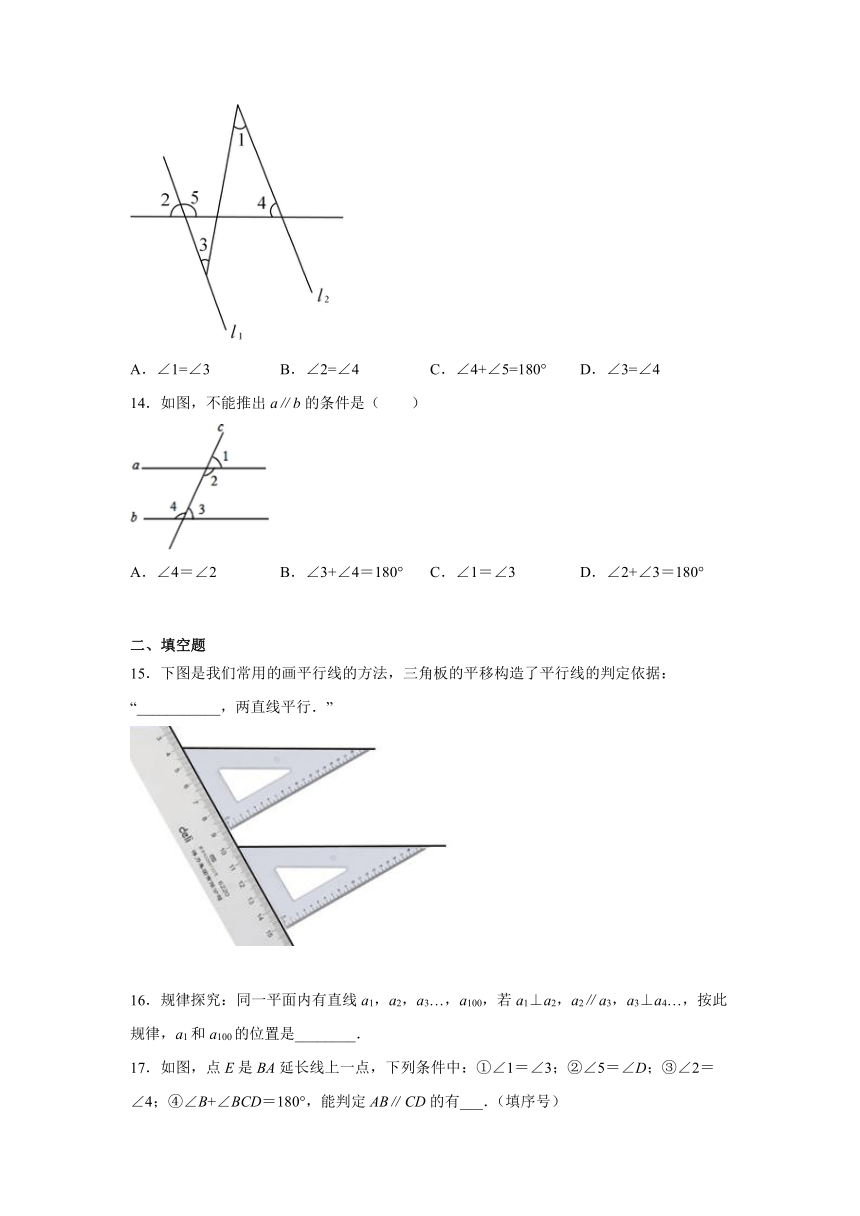
14.如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
二、填空题
15.下图是我们常用的画平行线的方法,三角板的平移构造了平行线的判定依据:“___________,两直线平行.”
16.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
17.如图,点E是BA延长线上一点,下列条件中:①∠1=∠3;②∠5=∠D;③∠2=∠4;④∠B+∠BCD=180°,能判定ABCD的有___.(填序号)
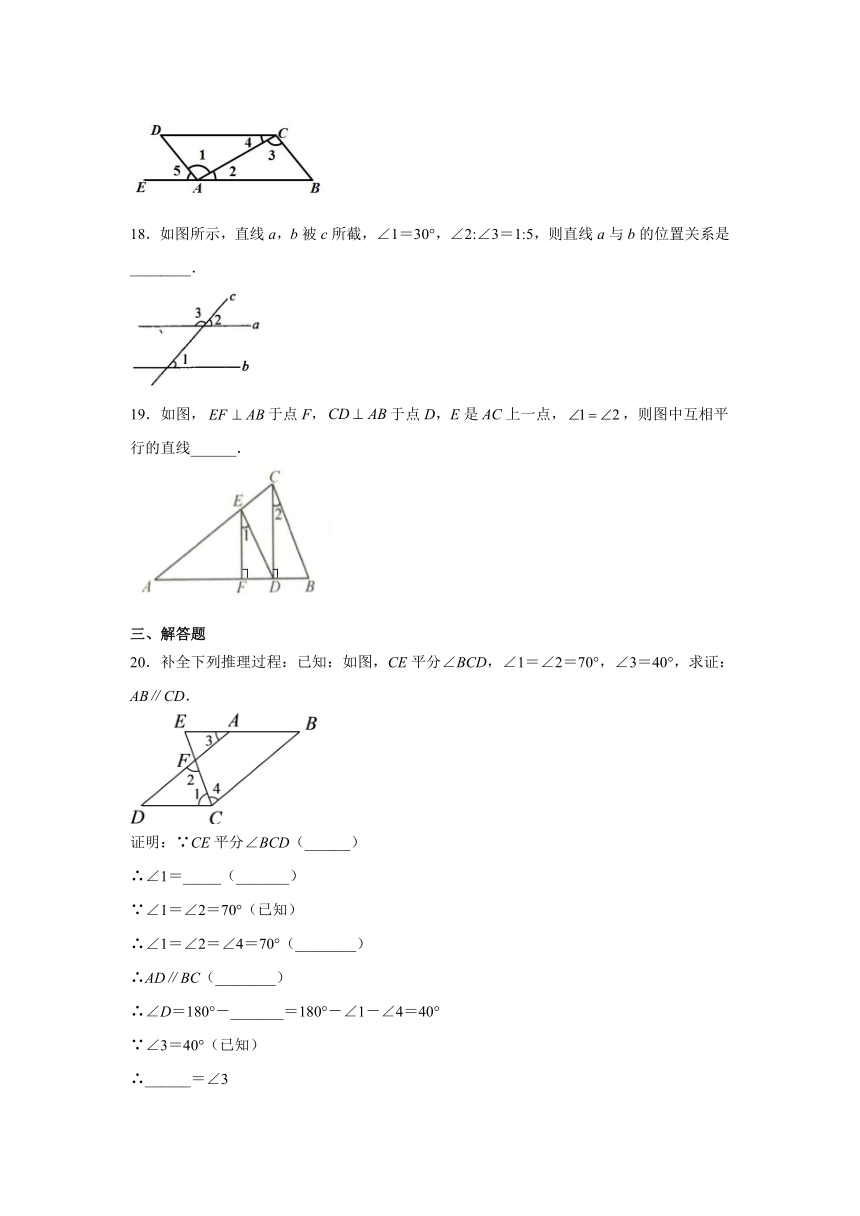
18.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
19.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线______.
三、解答题
20.补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
21.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知)
∠ABC=∠1 (① )
∴∠ABC=60°(等量代换)
又∵∠2=120°(已知)
∴(② )+∠2=180°(等式的性质)
∴AB∥CD (③ )
又∵∠2+∠BCD=(④ °)
∴∠BCD=60°(等式的性质)
∵∠D=60°(已知)
∴∠BCD=∠D (⑤ )
∴BC∥DE (⑥ )
22.已知:如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.
(1)如果∠2=∠3,那么____________.(____________,____________)
(2)如果∠2=∠5,那么____________.(____________,____________)
(3)如果∠2+∠1=180°,那么____________.(____________,____________)
(4)如果∠5=∠3,那么____________.(____________,____________)
23.完成下面的证明:
已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知)
∴∠ =90°( )
∵∠1=30°,∠B=60°(已知)
∴∠1+∠BAC+∠B= ( )
即∠ +∠B=180°
∴AD∥BC( )
参考答案
1--10AACBB DDAAD11--14 CADB
15.同位角相等
16.a1∥a100;
17.②③④
18.平行
19.,
20.证明:∵CE平分∠BCD( 已知 ),
∴∠1= ∠4 ( 角平分线定义 ),
∵∠1=∠2=70°已知,
∴∠1=∠2=∠4=70°(等量代换),
∴AD∥BC(内错角相等,两直线平行),
∴∠D=180°-∠BCD=180°-∠1-∠4=40°,
∵∠3=40°已知,
∴ ∠D =∠3,
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;∠4 ,角平分线定义 ;等量代换;内错角相等,两直线平行;∠BCD;∠D;内错角相等,两直线平行.
21解∵∠1=60°(已知)
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换),
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行),
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质),
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行),
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
22.(1)如果∠2=∠3,那么EF∥DC.(内错角相等,两直线平行);
(2)如果∠2=∠5,那么EF∥AB.(同位角相等,两直线平行);
(3)如果∠2+∠1=180°,那么AD∥BC.(同旁内角互补,两直线平行);
(4)如果∠5=∠3,那么AB∥CD.(内错角相等,两直线平行.
故答案为:(1)EFDG,内错角相等,两直线平行;(2)ABEF,同位角相等,两直线平行;(3)ADBC,同旁内角互补,两直线平行;(4)ABDG,内错角相等,两直线平行.
23.证明:∵(已知),
∴(垂直的定义),
∵,(已知),
∴(等量关系),
即,
∴(同旁内角互补,两直线平行).
2021--2022学年人教版七年级数学下册
一、单选题
1.如图,工人师傅用角尺画出工件边缘的垂线和,得到,理由是( )
A.在同一平面内,垂直于同一条直线的两条直线平行
B.在同一平面内,过一点有且仅有一条直线垂直于已知直线
C.连接直线外一点与直线各点的所有直线中,垂线段最短
D.经过直线外一点,有且只有一条直线与这条直线平行
2.已知,,是三条直线,下列结论正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
3.用反证法证明命题“在同一平面内,若 ,则 a∥c”时,首先应假设( )
A.a∥b B.b∥c C.a 与 c 相交 D.a 与 b
4.如图,现给出下列条件:① ,② ,③ ,④,⑤ .其中能够得到ABCD的条件的个数( )
A.2个 B.3个 C.4个 D.5个
5.如图所示,下列条件中,不能推出AB∥CE成立的条件是( )
A.∠A=∠ACE B.∠B=∠ACE C.∠B=∠ECD D.∠B+∠BCE=180°
6.如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
7.下列四个命题其中正确的个数是( )
①对顶角相等;②在同一平面内,若,与相交,则与也相交;③邻补角的平分线互相垂直;④在同一平面内,垂直于同一条直线的两条直线互相垂直
A.1个 B.2个 C.3个 D.4个
8.如图,下列四个结论:①∠1=∠3;②∠B=∠5;③∠B+∠BAD=180 ;④∠2=∠4;⑤∠D+∠BCD=180 .能判断AB∥CD的个数有 ( )
A.2个 B.3个 C.4个 D.5个
9.如图,下列选项中,不能得出直线的是( )
A.∠1=∠2 B.∠4=∠5 C.∠2+∠4=180° D.∠1=∠3
10.如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
11.如图,下列条件中能判断直线的是( )
A.∠1=∠2 B.∠1=∠5 C.∠2=∠4 D.∠3=∠5
12.如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
13.如图,下列条件中,不能判断∥的是( )
A.∠1=∠3 B.∠2=∠4 C.∠4+∠5=180° D.∠3=∠4
14.如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
二、填空题
15.下图是我们常用的画平行线的方法,三角板的平移构造了平行线的判定依据:“___________,两直线平行.”
16.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
17.如图,点E是BA延长线上一点,下列条件中:①∠1=∠3;②∠5=∠D;③∠2=∠4;④∠B+∠BCD=180°,能判定ABCD的有___.(填序号)
18.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
19.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线______.
三、解答题
20.补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
21.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知)
∠ABC=∠1 (① )
∴∠ABC=60°(等量代换)
又∵∠2=120°(已知)
∴(② )+∠2=180°(等式的性质)
∴AB∥CD (③ )
又∵∠2+∠BCD=(④ °)
∴∠BCD=60°(等式的性质)
∵∠D=60°(已知)
∴∠BCD=∠D (⑤ )
∴BC∥DE (⑥ )
22.已知:如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.
(1)如果∠2=∠3,那么____________.(____________,____________)
(2)如果∠2=∠5,那么____________.(____________,____________)
(3)如果∠2+∠1=180°,那么____________.(____________,____________)
(4)如果∠5=∠3,那么____________.(____________,____________)
23.完成下面的证明:
已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知)
∴∠ =90°( )
∵∠1=30°,∠B=60°(已知)
∴∠1+∠BAC+∠B= ( )
即∠ +∠B=180°
∴AD∥BC( )
参考答案
1--10AACBB DDAAD11--14 CADB
15.同位角相等
16.a1∥a100;
17.②③④
18.平行
19.,
20.证明:∵CE平分∠BCD( 已知 ),
∴∠1= ∠4 ( 角平分线定义 ),
∵∠1=∠2=70°已知,
∴∠1=∠2=∠4=70°(等量代换),
∴AD∥BC(内错角相等,两直线平行),
∴∠D=180°-∠BCD=180°-∠1-∠4=40°,
∵∠3=40°已知,
∴ ∠D =∠3,
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;∠4 ,角平分线定义 ;等量代换;内错角相等,两直线平行;∠BCD;∠D;内错角相等,两直线平行.
21解∵∠1=60°(已知)
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换),
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行),
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质),
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行),
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
22.(1)如果∠2=∠3,那么EF∥DC.(内错角相等,两直线平行);
(2)如果∠2=∠5,那么EF∥AB.(同位角相等,两直线平行);
(3)如果∠2+∠1=180°,那么AD∥BC.(同旁内角互补,两直线平行);
(4)如果∠5=∠3,那么AB∥CD.(内错角相等,两直线平行.
故答案为:(1)EFDG,内错角相等,两直线平行;(2)ABEF,同位角相等,两直线平行;(3)ADBC,同旁内角互补,两直线平行;(4)ABDG,内错角相等,两直线平行.
23.证明:∵(已知),
∴(垂直的定义),
∵,(已知),
∴(等量关系),
即,
∴(同旁内角互补,两直线平行).
