2021--2022学年人教版七年级数学下册5.3.2 命题、定理、证明提高练习 (word版含答案)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册5.3.2 命题、定理、证明提高练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 09:10:44 | ||
图片预览



文档简介
5.3.2命题、定理、证明提高练习
2021--2022学年人教版七年级数学下册
一、单选题
1.如图,与相交于点,则下列结论正确的是( )
A. B. C. D.
2.下列说法正确的是( )
A.命题是定理,但定理未必是命题 B.公理和定理都是真命题
C.定理和命题一样,有真有假 D.“取线段AB的中点C”是一个真命题
3.下列命题:①两条直线被第三条直线所截,同位角的平分线互相平行;②直线外一点到这条直线的垂线段,就是这一点到这条直线的距离;③有限小数是有理数,无限小数是无理数;④在平面内,过一点有且只有一条直线与已知直线垂直;⑤在平面内,过一点有且只有一条直线与已知直线平行. 是真命题的有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,,,为垂足,所以和重合,其理由是()
A.两点确定一条直线
B.过一点能做一条垂线
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
5.下列命题中是真命题的是
A.两条直线被第三条直线所截,同位角相等 B.两个锐角的和是锐角
C.点(3,2)到x轴的距离是2 D.若a>b,则>
6.如图,直线AB,CD相交于点O,已知∠AOC=80°,∠BOE:∠EOD=3:2,则∠AOE的度数是( )
A.100° B.116° C.120° D.132°
7.下列语句中,是命题的是( )
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①③④ D.②③④⑤
8.说明“若a是实数,则a2>0”是假命题,可以举的反例是( )
A.a=﹣1 B.a=1 C.a=0 D.a=2
9.“两条直线相交,有且只有一个交点”的题设是( ).
A.两条直线 B.交点
C.两条直线相交 D.只有一个交点
10.下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线a⊥b,b⊥c,则直线a与c不相交.
A.1个 B.2个 C.3个 D.4个
11.下列命题是假命题的有( )
①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.
A.1个 B.2个 C.3个 D.4个
12.下列说法中正确的是( )
A.两条射线组成的图形叫做角
B.小于平角的角可分为锐角和钝角两类
C.射线就是直线
D.两点之间的所有连线中,线段最短
13.下列说法:①两点确定一条直线;②连接两点的线段叫做两点的距离;③两点之间,线段最短;④由两条射线组成的图形叫做角;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
14.下列命题中,真命题的个数是( )
①同位角相等;②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c;③a,b,c是三条直线,若a∥b,b∥c,则a∥c;④过一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
二、填空题
15.命题“如果a2=b2,那么a=b.”的否命题是__________.
16.命题“两个全等三角形的面积相等”的逆命题是:______.该逆命题是一个____命题(填“真”或“假”).
17.两条直线被第三条直线所截构成的八个角中,共有___对同位角.
18.把命题“对顶角相等”改写为“如果……,那么……”的形式为___________ ,这是一个______命题(填“真”或“假”)
19.已知:如图,直线AB、CD被直线GH所截,,求证: AB // CD.
完成下面的证明:
证明:∵AB被直线GH所截,
∴
∵
∴
∴ // ( )(填推理的依据).
三、解答题
20.判断下列命题的真假,并给出证明
(1)两个锐角的和是钝角;
(2)若a>b,则a2>b2;
21.根据命题“两直线平行,内错角相等”,解决下列问题:
(1)写出逆命题;
(2)判断逆命题是真命题还是假命题;
(3)根据逆命题画出图形,写出已知、求证.
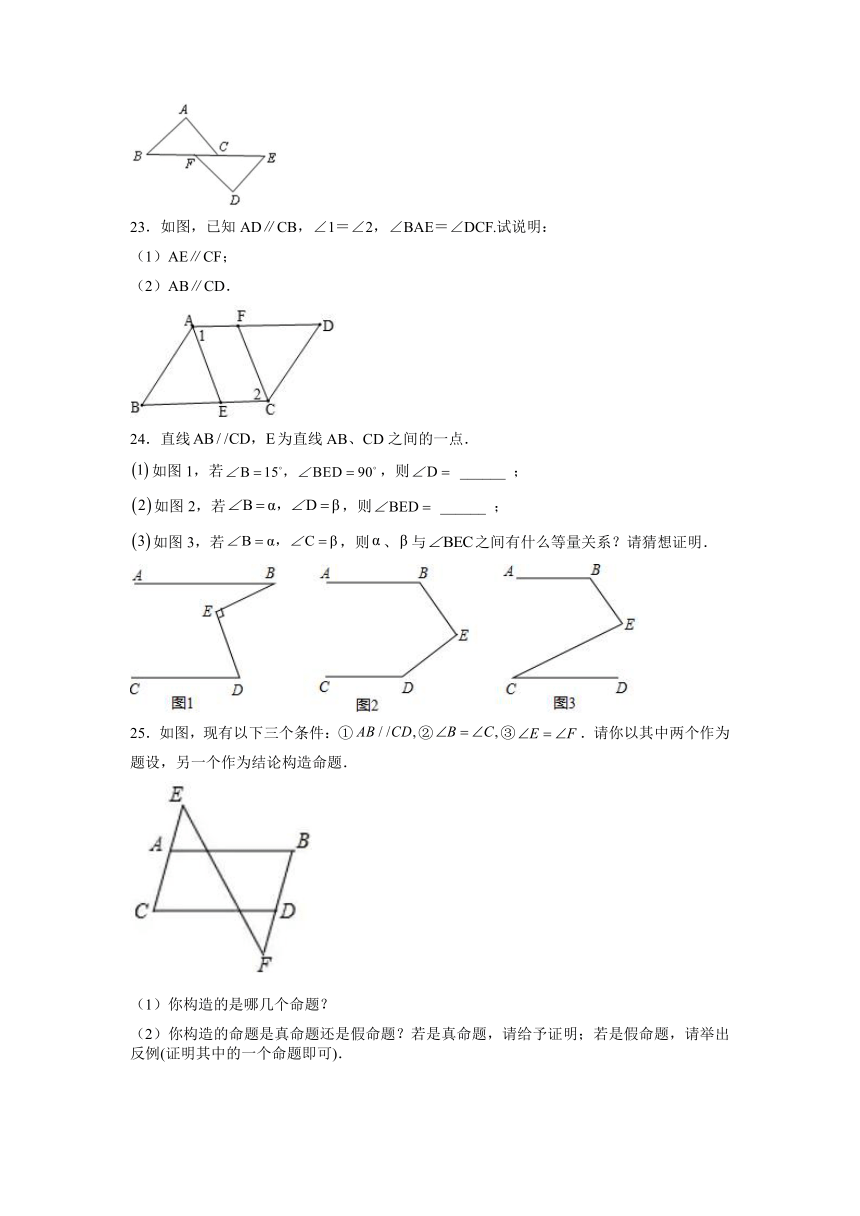
22.如图,点、、、在一条直线上,,,.
求证:.
23.如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF.试说明:
(1)AE∥CF;
(2)AB∥CD.
24.直线为直线AB、CD之间的一点.
如图1,若,则 ______ ;
如图2,若,则 ______ ;
如图3,若,则、与之间有什么等量关系?请猜想证明.
25.如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
参考答案
1--10ABADC DACCB 11--14CDBA
15.如果,那么
16.面积相等的两个三角形是全等三角形 假
17.4对.
18.如果两个角是对顶角,那么这两个角相等 真
19.证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠3=112°
∵∠2=68°,
∴∠2+∠3=180°,
∴AB∥CD,(同旁内角互补,两直线平行)
故答案为∠3,180°,AB,CD,同旁内角互补,两直线平行.
20.解:(1)两个锐角的和是钝角,是假命题,
例如,一个锐角是30°,另一个锐角是40°,
则这两个锐角的和是70°,70°不是钝角,
∴两个锐角的和是钝角,是假命题;
(2)若a>b,则a2>b2,是假命题,
例如:a=﹣1,b=﹣2,
a2=1,b2=4,
则a2<b2,
∴a>b,则a2>b2,是假命题.
21.解:(1)逆命题:内错角相等,两直线平行;
(2)是真命题;
(3)已知:如图,,
求证:.
22.解:点、、、共线,
∵,
∴.
∵,
∴.
∵,
∴.
在和中,
,,,
∴,
∴.
23.(1)∵AD∥CB (已知)
∴ ∠1=∠AEB (两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴ ∠AEB= ∠2(等量代换)
∴AE∥CF(同位角相等,两直线平行).
(2)∵三角形ABE的内角和是180
∴∠B+∠BAE+∠AEB=180
又∵∠AEB= ∠2(已证) ∠BAE=∠DCF(已知)
∴∠B+∠2+∠DCF=180 即∠B+∠BCD=180
∴AB∥CD(同旁内角互补,两直线平行).
24.(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β,
(3)猜想:∠BED=180°-α+β.
证明:过点E作EF∥AB,
则∠BEF=180°-∠B=180°-α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.
25.解:(1)有:如果那么;
如果那么;
如果,那么;
(2)如图:
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
∴如果那么为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
∴如果那么为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
∴如果,那么为真命题.
2021--2022学年人教版七年级数学下册
一、单选题
1.如图,与相交于点,则下列结论正确的是( )
A. B. C. D.
2.下列说法正确的是( )
A.命题是定理,但定理未必是命题 B.公理和定理都是真命题
C.定理和命题一样,有真有假 D.“取线段AB的中点C”是一个真命题
3.下列命题:①两条直线被第三条直线所截,同位角的平分线互相平行;②直线外一点到这条直线的垂线段,就是这一点到这条直线的距离;③有限小数是有理数,无限小数是无理数;④在平面内,过一点有且只有一条直线与已知直线垂直;⑤在平面内,过一点有且只有一条直线与已知直线平行. 是真命题的有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,,,为垂足,所以和重合,其理由是()
A.两点确定一条直线
B.过一点能做一条垂线
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
5.下列命题中是真命题的是
A.两条直线被第三条直线所截,同位角相等 B.两个锐角的和是锐角
C.点(3,2)到x轴的距离是2 D.若a>b,则>
6.如图,直线AB,CD相交于点O,已知∠AOC=80°,∠BOE:∠EOD=3:2,则∠AOE的度数是( )
A.100° B.116° C.120° D.132°
7.下列语句中,是命题的是( )
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①③④ D.②③④⑤
8.说明“若a是实数,则a2>0”是假命题,可以举的反例是( )
A.a=﹣1 B.a=1 C.a=0 D.a=2
9.“两条直线相交,有且只有一个交点”的题设是( ).
A.两条直线 B.交点
C.两条直线相交 D.只有一个交点
10.下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线a⊥b,b⊥c,则直线a与c不相交.
A.1个 B.2个 C.3个 D.4个
11.下列命题是假命题的有( )
①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.
A.1个 B.2个 C.3个 D.4个
12.下列说法中正确的是( )
A.两条射线组成的图形叫做角
B.小于平角的角可分为锐角和钝角两类
C.射线就是直线
D.两点之间的所有连线中,线段最短
13.下列说法:①两点确定一条直线;②连接两点的线段叫做两点的距离;③两点之间,线段最短;④由两条射线组成的图形叫做角;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
14.下列命题中,真命题的个数是( )
①同位角相等;②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c;③a,b,c是三条直线,若a∥b,b∥c,则a∥c;④过一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
二、填空题
15.命题“如果a2=b2,那么a=b.”的否命题是__________.
16.命题“两个全等三角形的面积相等”的逆命题是:______.该逆命题是一个____命题(填“真”或“假”).
17.两条直线被第三条直线所截构成的八个角中,共有___对同位角.
18.把命题“对顶角相等”改写为“如果……,那么……”的形式为___________ ,这是一个______命题(填“真”或“假”)
19.已知:如图,直线AB、CD被直线GH所截,,求证: AB // CD.
完成下面的证明:
证明:∵AB被直线GH所截,
∴
∵
∴
∴ // ( )(填推理的依据).
三、解答题
20.判断下列命题的真假,并给出证明
(1)两个锐角的和是钝角;
(2)若a>b,则a2>b2;
21.根据命题“两直线平行,内错角相等”,解决下列问题:
(1)写出逆命题;
(2)判断逆命题是真命题还是假命题;
(3)根据逆命题画出图形,写出已知、求证.
22.如图,点、、、在一条直线上,,,.
求证:.
23.如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF.试说明:
(1)AE∥CF;
(2)AB∥CD.
24.直线为直线AB、CD之间的一点.
如图1,若,则 ______ ;
如图2,若,则 ______ ;
如图3,若,则、与之间有什么等量关系?请猜想证明.
25.如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
参考答案
1--10ABADC DACCB 11--14CDBA
15.如果,那么
16.面积相等的两个三角形是全等三角形 假
17.4对.
18.如果两个角是对顶角,那么这两个角相等 真
19.证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠3=112°
∵∠2=68°,
∴∠2+∠3=180°,
∴AB∥CD,(同旁内角互补,两直线平行)
故答案为∠3,180°,AB,CD,同旁内角互补,两直线平行.
20.解:(1)两个锐角的和是钝角,是假命题,
例如,一个锐角是30°,另一个锐角是40°,
则这两个锐角的和是70°,70°不是钝角,
∴两个锐角的和是钝角,是假命题;
(2)若a>b,则a2>b2,是假命题,
例如:a=﹣1,b=﹣2,
a2=1,b2=4,
则a2<b2,
∴a>b,则a2>b2,是假命题.
21.解:(1)逆命题:内错角相等,两直线平行;
(2)是真命题;
(3)已知:如图,,
求证:.
22.解:点、、、共线,
∵,
∴.
∵,
∴.
∵,
∴.
在和中,
,,,
∴,
∴.
23.(1)∵AD∥CB (已知)
∴ ∠1=∠AEB (两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴ ∠AEB= ∠2(等量代换)
∴AE∥CF(同位角相等,两直线平行).
(2)∵三角形ABE的内角和是180
∴∠B+∠BAE+∠AEB=180
又∵∠AEB= ∠2(已证) ∠BAE=∠DCF(已知)
∴∠B+∠2+∠DCF=180 即∠B+∠BCD=180
∴AB∥CD(同旁内角互补,两直线平行).
24.(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β,
(3)猜想:∠BED=180°-α+β.
证明:过点E作EF∥AB,
则∠BEF=180°-∠B=180°-α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.
25.解:(1)有:如果那么;
如果那么;
如果,那么;
(2)如图:
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
∴如果那么为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
∴如果那么为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
∴如果,那么为真命题.
