2021-2022学年人教版八年级数学下册17.1勾股定理课后练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1勾股定理课后练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 09:18:17 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十七章勾股定理 17.1 勾股定理 课后练习
一、选择题
1.下列各组数中是勾股数的是( )
A.1,, B.,, C.,, D.,,
2.在平面直角坐标系中,已知点A(1,3)和点B(3,1),点C、D分别是x轴,y轴上的动点,则四边形ABCD的周长最小值为( )
A.5 B.6 C.2+2 D.8
3.如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC,BC为斜边作三个等腰直角△ABD,△ACE,△BCF,图中阴影部分的面积分别记为S1,S2,S3,S4,若已知Rt△ABC的面积,则下列代数式中,一定能求出确切值的代数式是( )
A.S4 B.S1+S4﹣S3 C.S2+S3+S4 D.S1+S2﹣S3
4. 中, 是垂足,与交于,则.
A. B. C. D.
5.在中,,,.下列关于的四种说法:①是无理数;②可以用数轴上的一个点来表示;③是8的算术平方根;④.其中,所有正确的说法的序号是( )
A.①②④ B.②③④ C.①②③ D.①③④
6.如图,四边形ABCD中,∠B=90°,CD=2,AE平分∠BAD,DE平分∠ADC,∠AED=120°,设AB=x,CE=y,则下列式子可以表示线段AD长的是( )
A.x+y+ B.x+y+2 C.x+y+2 D.x+y+
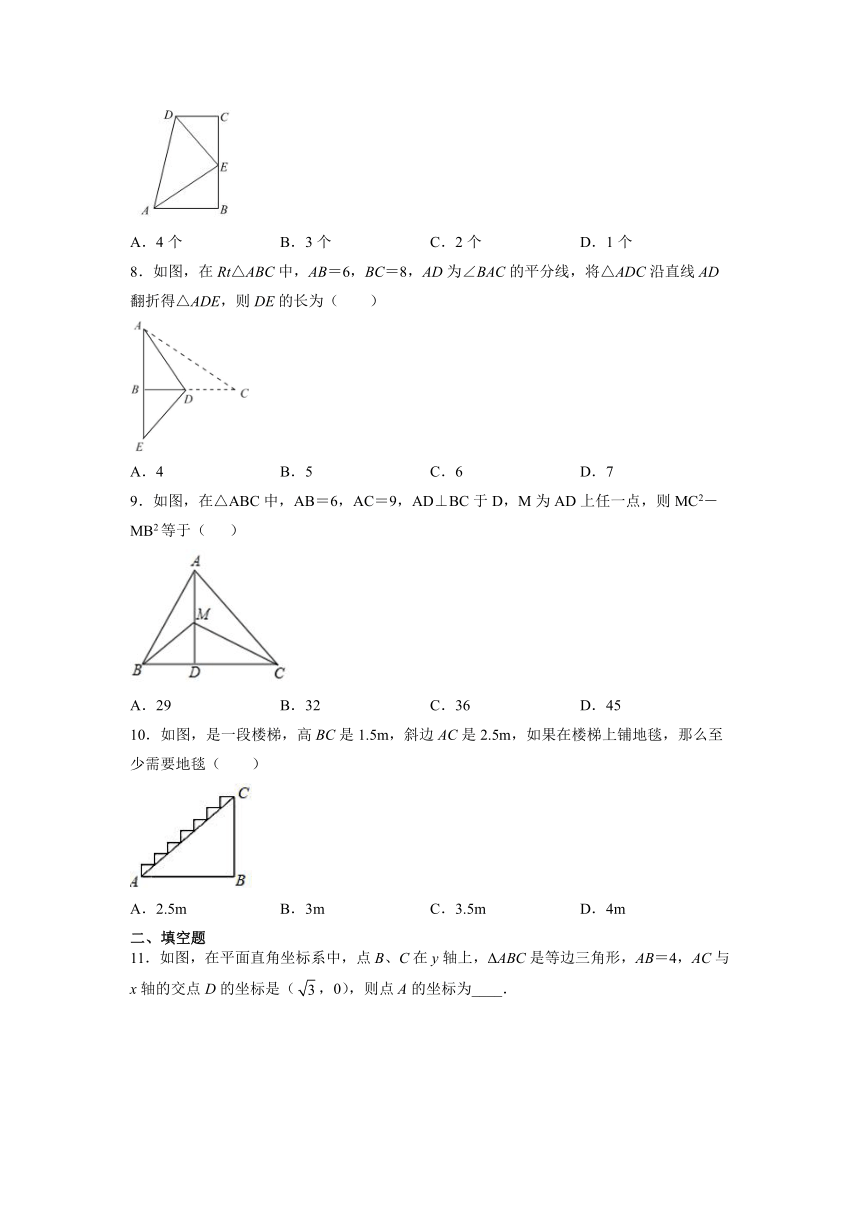
7.如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
(1)DE平分∠CDA;(2)△EBA≌△EDA;(3)△EBA≌△DCE;(4)AB+CD=AD;(5)AE2+DE2=AD2
A.4个 B.3个 C.2个 D.1个
8.如图,在Rt△ABC中,AB=6,BC=8,AD为∠BAC的平分线,将△ADC沿直线AD翻折得△ADE,则DE的长为( )
A.4 B.5 C.6 D.7
9.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
10.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m B.3m C.3.5m D.4m
二、填空题
11.如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是(,0),则点A的坐标为____.
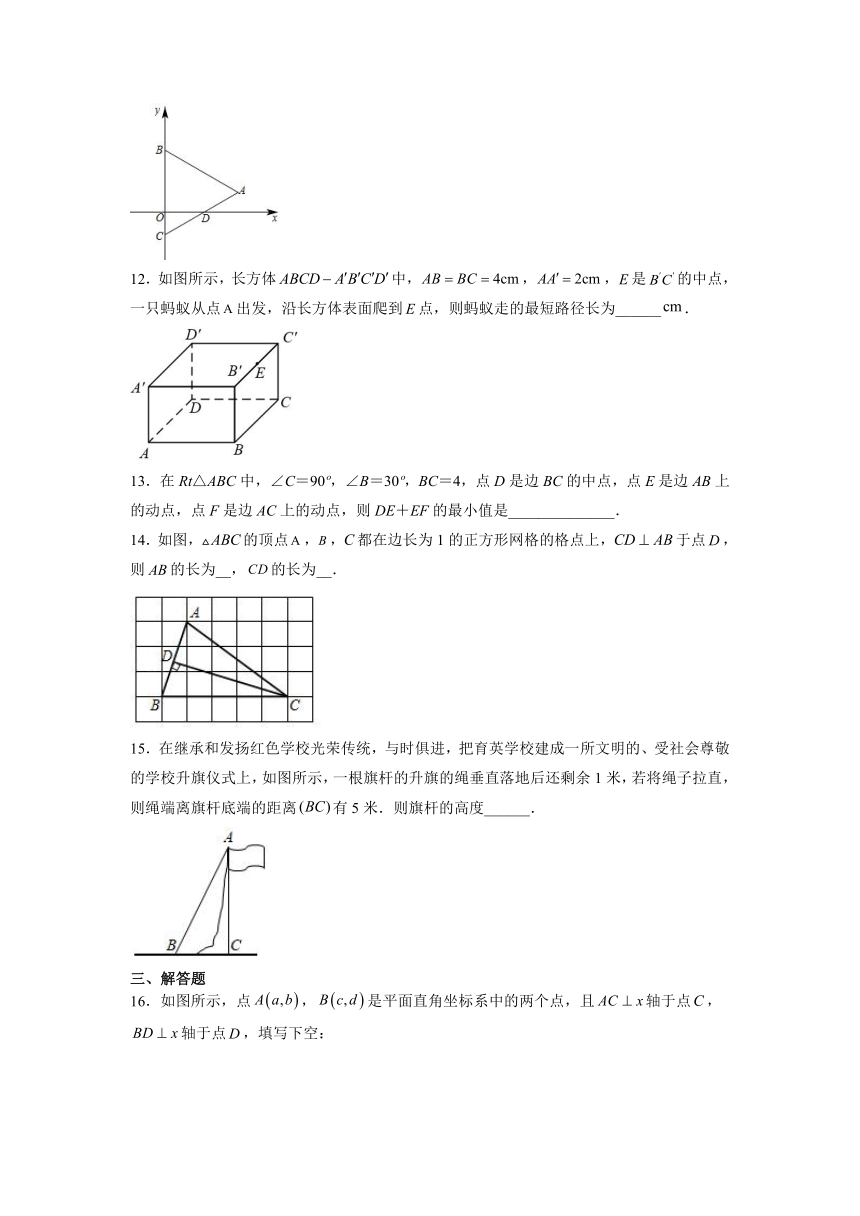
12.如图所示,长方体中,,,是的中点,一只蚂蚁从点出发,沿长方体表面爬到点,则蚂蚁走的最短路径长为______.
13.在Rt△ABC中,∠C=90 ,∠B=30 ,BC=4,点D是边BC的中点,点E是边AB上的动点,点F是边AC上的动点,则DE+EF的最小值是______________.
14.如图,的顶点,,都在边长为1的正方形网格的格点上,于点,则的长为__,的长为__.
15.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度______.
三、解答题
16.如图所示,点,是平面直角坐标系中的两个点,且轴于点,轴于点,填写下空:
(1)_______,______(用含,,,的式子表示请注意字母的正负号)
(2)请构造直角三角形,利用勾股定理计算、两点之间的距离的平方为__________________.(用含,,,的式子表示)
(3)若,,求、两点之间的距离.
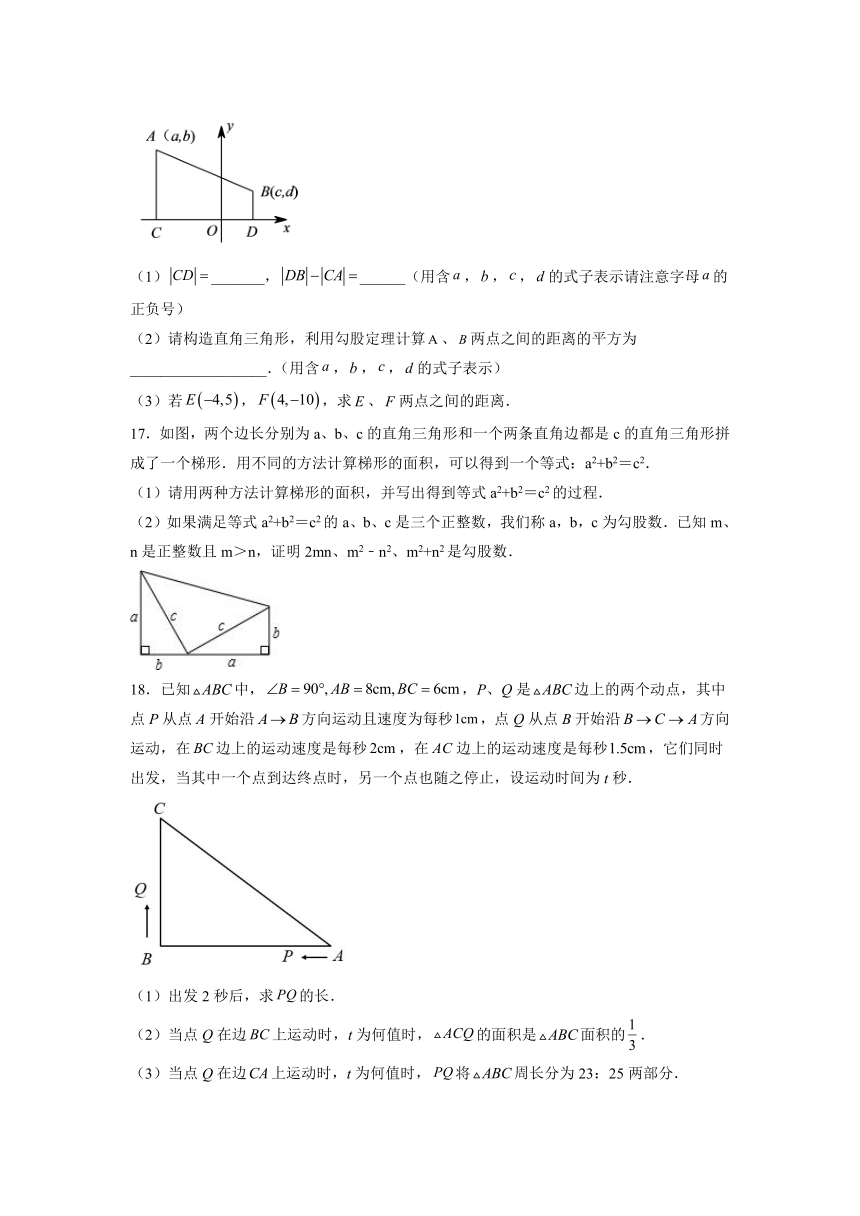
17.如图,两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成了一个梯形.用不同的方法计算梯形的面积,可以得到一个等式:a2+b2=c2.
(1)请用两种方法计算梯形的面积,并写出得到等式a2+b2=c2的过程.
(2)如果满足等式a2+b2=c2的a、b、c是三个正整数,我们称a,b,c为勾股数.已知m、n是正整数且m>n,证明2mn、m2﹣n2、m2+n2是勾股数.
18.已知中,,P、Q是边上的两个动点,其中点P从点A开始沿方向运动且速度为每秒,点Q从点B开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒.
(1)出发2秒后,求的长.
(2)当点Q在边上运动时,t为何值时,的面积是面积的.
(3)当点Q在边上运动时,t为何值时,将周长分为23:25两部分.
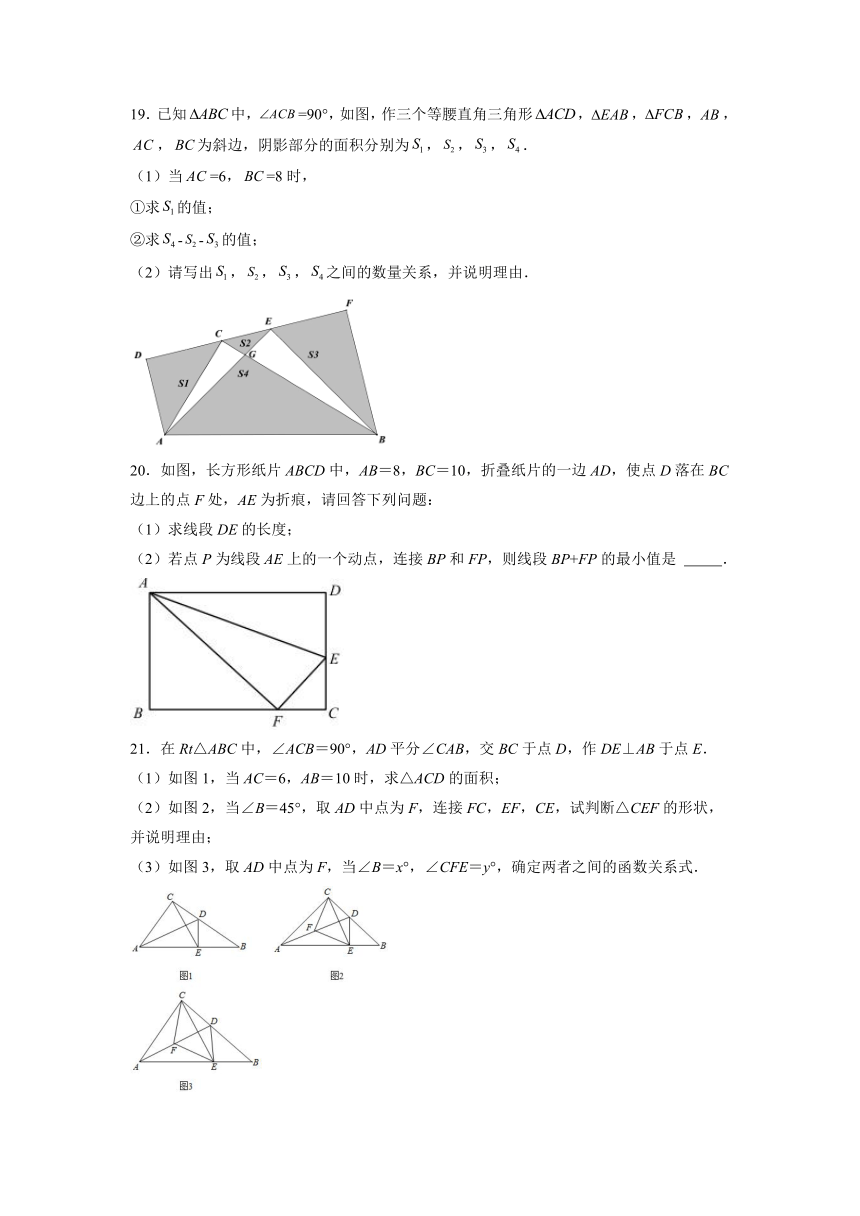
19.已知中,=90°,如图,作三个等腰直角三角形,,,,,为斜边,阴影部分的面积分别为,,,.
(1)当=6,=8时,
①求的值;
②求--的值;
(2)请写出,,,之间的数量关系,并说明理由.
20.如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题:
(1)求线段DE的长度;
(2)若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .
21.在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交BC于点D,作DE⊥AB于点E.
(1)如图1,当AC=6,AB=10时,求△ACD的面积;
(2)如图2,当∠B=45°,取AD中点为F,连接FC,EF,CE,试判断△CEF的形状,并说明理由;
(3)如图3,取AD中点为F,当∠B=x°,∠CFE=y°,确定两者之间的函数关系式.
22.如图,已知,数轴上点A表示的数为a.
(1)求出数轴上点A所表示的数a.
(2)比较点A所表示的数a与的大小.
(3)求的值.
23.如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
【参考答案】
1.B 2.B 3.A 4.A 5.C 6.B 7.B 8.B 9.D 10.C
11.
12.
13.3
14.
15.12米
16.(1),
∵,,
∴.
故答案为:c-a,d-b.
(2)如图,过点B作BE⊥AC于E.
则|BE|=|CD|=c-a,|AE|=|DB|-|CA|=d-b
在Rt△ABE中,由勾股定理得:.
故答案为:
(3)由(2)得:,
所以.
17.解:(1)根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2;
(2)证明:∵(2mn)2+(m2﹣n2)2=4m2n2+m4﹣2m2n2+n4=m4+2m2n2+n4=(m2+n2)2,
∵m、n是正整数且m>n,
∴2mn、m2﹣n2、m2+n2是勾股数.
18.(1)解:当出发2秒后,AP=2,BQ=4,
∴BP=AB-AP=8-2=6,
∵∠B=90°,
∴(cm)
(2)解:∵BQ=2t,BC=6,
∴CQ=6-2t,
∴,
得t=2;
(3)解:在中,,
∴10,
当点Q在AC上时,,
∵BC=6,BP=8-t,
∴PQ分△ABC的周长中BP+BC+CQ=,AP+AQ=,
当时,得t=4;
当时,得t=6;
检验可得t值均符合题意,
∴t为4或6时,将周长分为23:25两部分.
19.解:(1)①是等腰直角三角形,=6,
==,
;
②=90°,=6,=8,
=10,
和是等腰直角三角形,
,,
设
;
(2)设,
如图,等腰直角三角形的面积公式,
∵等腰直角三角形,,,
∴,
∵,
∴,即,
∴,
∴.
20.解:(1)长方形纸片ABCD中,折叠纸片,使点D落在BC边上的点F处,
则AF=AD=BC=10,
BF=,
FC=BC BF=10 6=4,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴DE=EF,
设DE=EF=x,
则EC=DC DE=8 x,
又∵△EFC为直角三角形,
∴FC2+EC2=FE2,
即42+(8 x)2=x2,
∴x=5,
∴DE=5;
(2)连接BP,PF,PD,BD,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴D、F关于AE对称,
∴PF=PD,
则BP+PF=BP+PD≥BD,
∴BP+PF最小为BD,
BD=,
∴BP+PF最小值为:.
故答案为:.
21.(1)∵∠ACB=90°,AC=6,AB=10,
∴BC===8,
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AD=AE=6,BE=4,
令CD=x,则DE=x,DB=8﹣x,
∵DE2+BE2=BD2,
∴x2+42=(8﹣x)2,
解得x=3,
∴DE=3,
∴S△ACD=AC CD=×6×3=9.
(2)解:△CEF为等腰直角三角形.
∵DE⊥AB,
∴∠AED=90°,
∵∠ACB=90°,F为AD的中点,
∴CF=AF=DF=EF=AD,
∴∠CAF=∠ACF,∠FAE=∠AEF,
∵∠B=45°,AD平分∠CAB,
∴∠CAF=∠EAF=22.5°,
∴∠CFD=∠ACF+∠CAF=2∠CAF=45°,
∠EFD=∠EAF+∠AEF=2∠EAF=45°,
∵∠CFE=∠CFD+∠EFD=2∠CAF+2∠CAF=90°,
∴△CEF为等腰直角三角形.
(3)由(2)知∠CFE=2∠CAF+2∠CAF=2∠CAB=2(90°﹣x),
∴y=2(90﹣x)=180﹣2x.
22.(1)由数轴可知:.
∴数轴上点A所表示的数a为:;
(2)∵,,,
∴,
∴,
即;
(3),,
则
.
23.如图,
由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC= (米),
所以飞机飞行的速度为 (千米/小时)
一、选择题
1.下列各组数中是勾股数的是( )
A.1,, B.,, C.,, D.,,
2.在平面直角坐标系中,已知点A(1,3)和点B(3,1),点C、D分别是x轴,y轴上的动点,则四边形ABCD的周长最小值为( )
A.5 B.6 C.2+2 D.8
3.如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC,BC为斜边作三个等腰直角△ABD,△ACE,△BCF,图中阴影部分的面积分别记为S1,S2,S3,S4,若已知Rt△ABC的面积,则下列代数式中,一定能求出确切值的代数式是( )
A.S4 B.S1+S4﹣S3 C.S2+S3+S4 D.S1+S2﹣S3
4. 中, 是垂足,与交于,则.
A. B. C. D.
5.在中,,,.下列关于的四种说法:①是无理数;②可以用数轴上的一个点来表示;③是8的算术平方根;④.其中,所有正确的说法的序号是( )
A.①②④ B.②③④ C.①②③ D.①③④
6.如图,四边形ABCD中,∠B=90°,CD=2,AE平分∠BAD,DE平分∠ADC,∠AED=120°,设AB=x,CE=y,则下列式子可以表示线段AD长的是( )
A.x+y+ B.x+y+2 C.x+y+2 D.x+y+
7.如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
(1)DE平分∠CDA;(2)△EBA≌△EDA;(3)△EBA≌△DCE;(4)AB+CD=AD;(5)AE2+DE2=AD2
A.4个 B.3个 C.2个 D.1个
8.如图,在Rt△ABC中,AB=6,BC=8,AD为∠BAC的平分线,将△ADC沿直线AD翻折得△ADE,则DE的长为( )
A.4 B.5 C.6 D.7
9.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
10.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m B.3m C.3.5m D.4m
二、填空题
11.如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是(,0),则点A的坐标为____.
12.如图所示,长方体中,,,是的中点,一只蚂蚁从点出发,沿长方体表面爬到点,则蚂蚁走的最短路径长为______.
13.在Rt△ABC中,∠C=90 ,∠B=30 ,BC=4,点D是边BC的中点,点E是边AB上的动点,点F是边AC上的动点,则DE+EF的最小值是______________.
14.如图,的顶点,,都在边长为1的正方形网格的格点上,于点,则的长为__,的长为__.
15.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度______.
三、解答题
16.如图所示,点,是平面直角坐标系中的两个点,且轴于点,轴于点,填写下空:
(1)_______,______(用含,,,的式子表示请注意字母的正负号)
(2)请构造直角三角形,利用勾股定理计算、两点之间的距离的平方为__________________.(用含,,,的式子表示)
(3)若,,求、两点之间的距离.
17.如图,两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成了一个梯形.用不同的方法计算梯形的面积,可以得到一个等式:a2+b2=c2.
(1)请用两种方法计算梯形的面积,并写出得到等式a2+b2=c2的过程.
(2)如果满足等式a2+b2=c2的a、b、c是三个正整数,我们称a,b,c为勾股数.已知m、n是正整数且m>n,证明2mn、m2﹣n2、m2+n2是勾股数.
18.已知中,,P、Q是边上的两个动点,其中点P从点A开始沿方向运动且速度为每秒,点Q从点B开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒.
(1)出发2秒后,求的长.
(2)当点Q在边上运动时,t为何值时,的面积是面积的.
(3)当点Q在边上运动时,t为何值时,将周长分为23:25两部分.
19.已知中,=90°,如图,作三个等腰直角三角形,,,,,为斜边,阴影部分的面积分别为,,,.
(1)当=6,=8时,
①求的值;
②求--的值;
(2)请写出,,,之间的数量关系,并说明理由.
20.如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题:
(1)求线段DE的长度;
(2)若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .
21.在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交BC于点D,作DE⊥AB于点E.
(1)如图1,当AC=6,AB=10时,求△ACD的面积;
(2)如图2,当∠B=45°,取AD中点为F,连接FC,EF,CE,试判断△CEF的形状,并说明理由;
(3)如图3,取AD中点为F,当∠B=x°,∠CFE=y°,确定两者之间的函数关系式.
22.如图,已知,数轴上点A表示的数为a.
(1)求出数轴上点A所表示的数a.
(2)比较点A所表示的数a与的大小.
(3)求的值.
23.如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
【参考答案】
1.B 2.B 3.A 4.A 5.C 6.B 7.B 8.B 9.D 10.C
11.
12.
13.3
14.
15.12米
16.(1),
∵,,
∴.
故答案为:c-a,d-b.
(2)如图,过点B作BE⊥AC于E.
则|BE|=|CD|=c-a,|AE|=|DB|-|CA|=d-b
在Rt△ABE中,由勾股定理得:.
故答案为:
(3)由(2)得:,
所以.
17.解:(1)根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2;
(2)证明:∵(2mn)2+(m2﹣n2)2=4m2n2+m4﹣2m2n2+n4=m4+2m2n2+n4=(m2+n2)2,
∵m、n是正整数且m>n,
∴2mn、m2﹣n2、m2+n2是勾股数.
18.(1)解:当出发2秒后,AP=2,BQ=4,
∴BP=AB-AP=8-2=6,
∵∠B=90°,
∴(cm)
(2)解:∵BQ=2t,BC=6,
∴CQ=6-2t,
∴,
得t=2;
(3)解:在中,,
∴10,
当点Q在AC上时,,
∵BC=6,BP=8-t,
∴PQ分△ABC的周长中BP+BC+CQ=,AP+AQ=,
当时,得t=4;
当时,得t=6;
检验可得t值均符合题意,
∴t为4或6时,将周长分为23:25两部分.
19.解:(1)①是等腰直角三角形,=6,
==,
;
②=90°,=6,=8,
=10,
和是等腰直角三角形,
,,
设
;
(2)设,
如图,等腰直角三角形的面积公式,
∵等腰直角三角形,,,
∴,
∵,
∴,即,
∴,
∴.
20.解:(1)长方形纸片ABCD中,折叠纸片,使点D落在BC边上的点F处,
则AF=AD=BC=10,
BF=,
FC=BC BF=10 6=4,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴DE=EF,
设DE=EF=x,
则EC=DC DE=8 x,
又∵△EFC为直角三角形,
∴FC2+EC2=FE2,
即42+(8 x)2=x2,
∴x=5,
∴DE=5;
(2)连接BP,PF,PD,BD,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴D、F关于AE对称,
∴PF=PD,
则BP+PF=BP+PD≥BD,
∴BP+PF最小为BD,
BD=,
∴BP+PF最小值为:.
故答案为:.
21.(1)∵∠ACB=90°,AC=6,AB=10,
∴BC===8,
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AD=AE=6,BE=4,
令CD=x,则DE=x,DB=8﹣x,
∵DE2+BE2=BD2,
∴x2+42=(8﹣x)2,
解得x=3,
∴DE=3,
∴S△ACD=AC CD=×6×3=9.
(2)解:△CEF为等腰直角三角形.
∵DE⊥AB,
∴∠AED=90°,
∵∠ACB=90°,F为AD的中点,
∴CF=AF=DF=EF=AD,
∴∠CAF=∠ACF,∠FAE=∠AEF,
∵∠B=45°,AD平分∠CAB,
∴∠CAF=∠EAF=22.5°,
∴∠CFD=∠ACF+∠CAF=2∠CAF=45°,
∠EFD=∠EAF+∠AEF=2∠EAF=45°,
∵∠CFE=∠CFD+∠EFD=2∠CAF+2∠CAF=90°,
∴△CEF为等腰直角三角形.
(3)由(2)知∠CFE=2∠CAF+2∠CAF=2∠CAB=2(90°﹣x),
∴y=2(90﹣x)=180﹣2x.
22.(1)由数轴可知:.
∴数轴上点A所表示的数a为:;
(2)∵,,,
∴,
∴,
即;
(3),,
则
.
23.如图,
由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC= (米),
所以飞机飞行的速度为 (千米/小时)
