2021-2022学年人教版八年级数学下册17.2 勾股定理的逆定理课后练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.2 勾股定理的逆定理课后练习 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 153.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 09:20:47 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学下册 第十七章 勾股定理
17.2 勾股定理的逆定理课后练习
一、选择题
1.满足下列条件的△ABC,不是直角三角形的是( )
A.∠A:∠B:∠C=5:12:13 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.b2=a2﹣c2
2.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为( )
A.北偏西 B.南偏西75°
C.南偏东或北偏西 D.南偏西或北偏东
3.如图,在△ABC中,AD⊥BC于点D,BD=9,AD=12,AC=20,则△ABC是( )
A.等腰三角形 B.任意三角形
C.直角三角形 D.无法确定
4.如图所示的网格是正方形网格,则∠PAB+∠PBA( )度(点A,B,P是网格线交点)
A.30 B.45 C.60 D.90
5.如图,每个小正方形的边长都相等,A,B,C是小正方形的顶点,则的度数为( )
A. B. C. D.
6.如图,在四边形ABCD中,,,,,则四边形ABCD的面积是( ).
A.6 B.8 C.10 D.12
7.如图,在四边形中,,,,,,则四边形的面积为( )
A.122 B.114 C.110 D.100
8.如图,四边形中,,,,,,则四边形的面积为( )
A.100 B.110 C.114 D.122
9.如图,在四边形中,, ,,,则四边形的面积是( )
A. B.
C. D.
10.如图1,园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24米2 B.36米2 C.48米2 D.72米2
二、填空题
11.已知在中,,,,则的面积为_______.
12.在△ABC中,AC=5,BC=12,AB=13,则AB边上的高为=___.
13.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
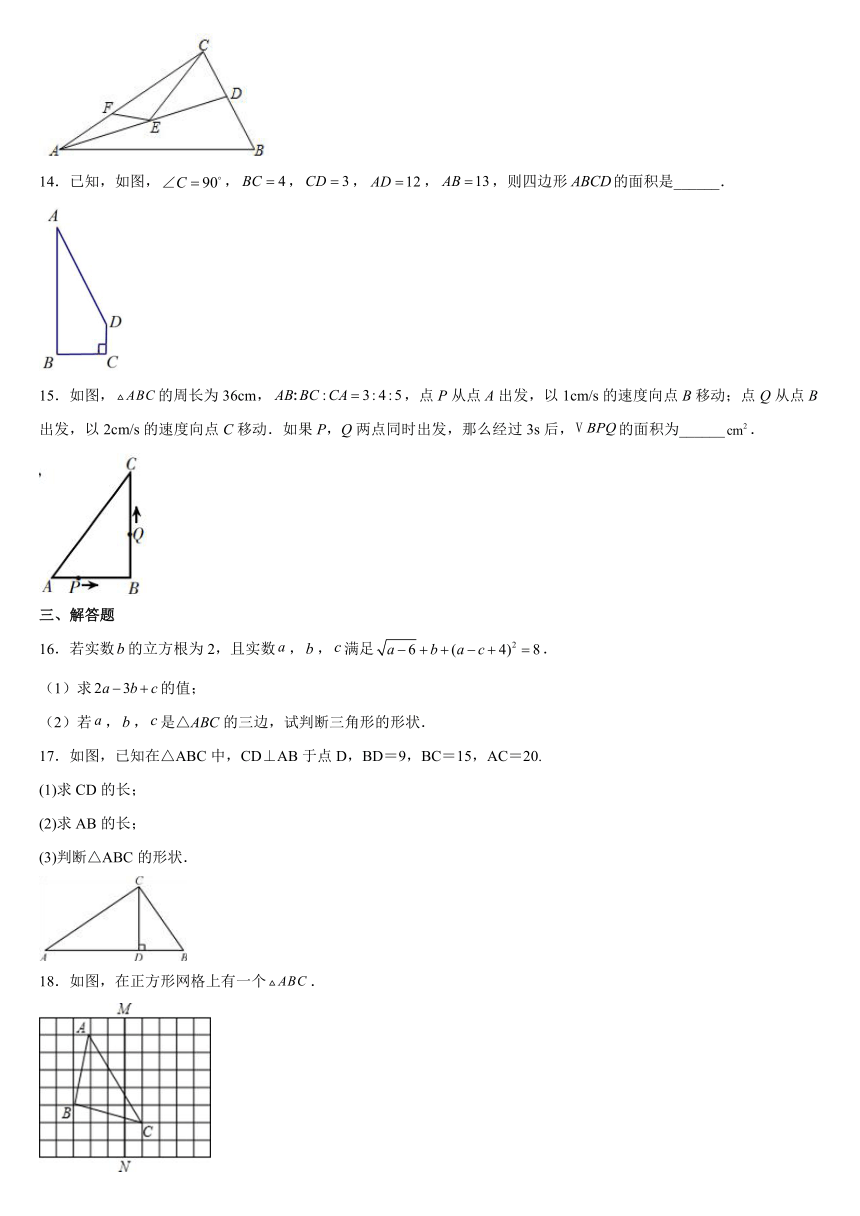
14.已知,如图,,,,,,则四边形的面积是______.
15.如图,的周长为36cm,,点P从点A出发,以1cm/s的速度向点B移动;点Q从点B出发,以2cm/s的速度向点C移动.如果P,Q两点同时出发,那么经过3s后,的面积为______.
三、解答题
16.若实数的立方根为2,且实数,,满足.
(1)求的值;
(2)若,,是△ABC的三边,试判断三角形的形状.
17.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
18.如图,在正方形网格上有一个.
(1)发现与的数量关系是 ,位置关系是 .
(2)画关于直线的对称图形(不写画法);
(3)若网格上的每个小正方形的边长为1,则的面积为 .
(4)在直线MN上找一点P,使PA+PB最短.
19.如图,四边形ABCD中,∠A=90°,AB=AD=,CD=3,BC=.
(1)求∠ADC的度数.
(2)求四边形ABCD的面积.
20.如图,小明家A和地铁口B两地恰好处在东西方向上,且相距3km,学校C在他家正北方向的4km处,公园D与地铁口和学校的距离分别5km和5km.
(1)求地铁口、公园和学校三地组成的∠BDC的大小;
(2)计算公园与小明家的距离.
21.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
22.阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若,则该三角形是直角三角形;②若,则该三角形是钝角三角形;③若,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.
(2)若一个三角形的三边长分别是5,12,x.且这个三角形是直角三角形,求的值.
(3)当,时,判断的形状,并求出对应的的取值范围.
23.阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若a2=b2+c2,则该三角形是直角三角形;②若a2b2+c2,则该三角形是钝角三角形;③若a2b2+c2,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,62=3642+52,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是 三角形.
(2)若一个三角形的三边长分别是5,12,x,且这个三角形是直角三角形,则x的值为 .
(3)若一个三角形的三边长为a=,b=,c=,其中a是最长边,请判断这个三角形的形状,并写出你的判断过程.
【参考答案】
1.A 2.C 3.C 4.B 5.A 6.B 7.B 8.C 9.A 10.B
11.84
12.
13.4.8
14.36
15.18
16.(1);(2)△ABC是直角三角形.
17.(1)CD长为12;(2)AB的长为25;(3)△ABC是直角三角形
18.(1);;(2)略;(3)8.5;(4)略
19.(1)135°;(2)4
20.(1)∠BDC=45°;(2)公园与小明家的距离为km.
21.解:(1)是; (2)新路CH比原路CA少0.05千米.
22.(1)锐角;(2)169或119;(3)略
23.(1)锐角;(2)13或;(3)钝角三角形
17.2 勾股定理的逆定理课后练习
一、选择题
1.满足下列条件的△ABC,不是直角三角形的是( )
A.∠A:∠B:∠C=5:12:13 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.b2=a2﹣c2
2.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为( )
A.北偏西 B.南偏西75°
C.南偏东或北偏西 D.南偏西或北偏东
3.如图,在△ABC中,AD⊥BC于点D,BD=9,AD=12,AC=20,则△ABC是( )
A.等腰三角形 B.任意三角形
C.直角三角形 D.无法确定
4.如图所示的网格是正方形网格,则∠PAB+∠PBA( )度(点A,B,P是网格线交点)
A.30 B.45 C.60 D.90
5.如图,每个小正方形的边长都相等,A,B,C是小正方形的顶点,则的度数为( )
A. B. C. D.
6.如图,在四边形ABCD中,,,,,则四边形ABCD的面积是( ).
A.6 B.8 C.10 D.12
7.如图,在四边形中,,,,,,则四边形的面积为( )
A.122 B.114 C.110 D.100
8.如图,四边形中,,,,,,则四边形的面积为( )
A.100 B.110 C.114 D.122
9.如图,在四边形中,, ,,,则四边形的面积是( )
A. B.
C. D.
10.如图1,园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24米2 B.36米2 C.48米2 D.72米2
二、填空题
11.已知在中,,,,则的面积为_______.
12.在△ABC中,AC=5,BC=12,AB=13,则AB边上的高为=___.
13.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
14.已知,如图,,,,,,则四边形的面积是______.
15.如图,的周长为36cm,,点P从点A出发,以1cm/s的速度向点B移动;点Q从点B出发,以2cm/s的速度向点C移动.如果P,Q两点同时出发,那么经过3s后,的面积为______.
三、解答题
16.若实数的立方根为2,且实数,,满足.
(1)求的值;
(2)若,,是△ABC的三边,试判断三角形的形状.
17.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
18.如图,在正方形网格上有一个.
(1)发现与的数量关系是 ,位置关系是 .
(2)画关于直线的对称图形(不写画法);
(3)若网格上的每个小正方形的边长为1,则的面积为 .
(4)在直线MN上找一点P,使PA+PB最短.
19.如图,四边形ABCD中,∠A=90°,AB=AD=,CD=3,BC=.
(1)求∠ADC的度数.
(2)求四边形ABCD的面积.
20.如图,小明家A和地铁口B两地恰好处在东西方向上,且相距3km,学校C在他家正北方向的4km处,公园D与地铁口和学校的距离分别5km和5km.
(1)求地铁口、公园和学校三地组成的∠BDC的大小;
(2)计算公园与小明家的距离.
21.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
22.阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若,则该三角形是直角三角形;②若,则该三角形是钝角三角形;③若,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.
(2)若一个三角形的三边长分别是5,12,x.且这个三角形是直角三角形,求的值.
(3)当,时,判断的形状,并求出对应的的取值范围.
23.阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若a2=b2+c2,则该三角形是直角三角形;②若a2b2+c2,则该三角形是钝角三角形;③若a2b2+c2,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,62=3642+52,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是 三角形.
(2)若一个三角形的三边长分别是5,12,x,且这个三角形是直角三角形,则x的值为 .
(3)若一个三角形的三边长为a=,b=,c=,其中a是最长边,请判断这个三角形的形状,并写出你的判断过程.
【参考答案】
1.A 2.C 3.C 4.B 5.A 6.B 7.B 8.C 9.A 10.B
11.84
12.
13.4.8
14.36
15.18
16.(1);(2)△ABC是直角三角形.
17.(1)CD长为12;(2)AB的长为25;(3)△ABC是直角三角形
18.(1);;(2)略;(3)8.5;(4)略
19.(1)135°;(2)4
20.(1)∠BDC=45°;(2)公园与小明家的距离为km.
21.解:(1)是; (2)新路CH比原路CA少0.05千米.
22.(1)锐角;(2)169或119;(3)略
23.(1)锐角;(2)13或;(3)钝角三角形
