2021-2022学年人教版八年级数学下册19.2.2 一次函数 随堂训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册19.2.2 一次函数 随堂训练 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 00:00:00 | ||
图片预览


文档简介
19.2.2《一次函数》随堂训练
2021-2022学年人教版八年级数学下册
一、单选题
1.下列一次函数中,y随x增大而增大的有( )
①;②;③;④;⑤.
A.①②③ B.①②⑤ C.①③⑤ D.①④⑤
2.函数的图象过点( ).
A. B. C. D.
3.直线与x轴的交点是,则k的值是( )
A.3 B.2 C. D.
4.一次函数(,为常数)的图象如图所示,则的取值范围是( )
A., B.,
C., D.,
5.下列图象中,以方程﹣2x+y﹣2=0的解为坐标的点组成的图象是( )
A. B. C. D.
6.要从直线得到直线,就要把直线( )
A.向上平移个单位 B.向下平移个单位
C.向左平移个单位 D.向右平移个单位
7.一次函数的图象与两坐标轴交于点A、B,则的面积等于( ).
A.18 B.12 C.9 D.6
8.一次函数的图象不经过( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知直线与直线平行,且直线l经过第二,三、四象限,则b的取值范围为( )
A. B. C. D.
10.某一次函数的图象经过点(,2),且函数的值随自变量x的增大而减小,则下列函数符合条件的是( )
A.y=4x+6 B.y=-x C.y=-x+1 D.y=-3x+5
二、填空题
11.直线与x轴交点坐标为_______,与y轴交点坐标为_______,图象经过_______象限,y随x的增大而_______.
12.直线经过点和点,若,则_____.
13.若一次函数的图象与y轴的交点在x轴的下方,则m的取值范围是_______.
14.直线平行于直线,且过点,则其解析式为________.
15.如图,直线是一次函数的图象,填空:
(1)当时,______;
(2)当时,______.
16.已知一次函数y=2x-a与y=3x+b的图象交于轴上原点外的一点,则=________.
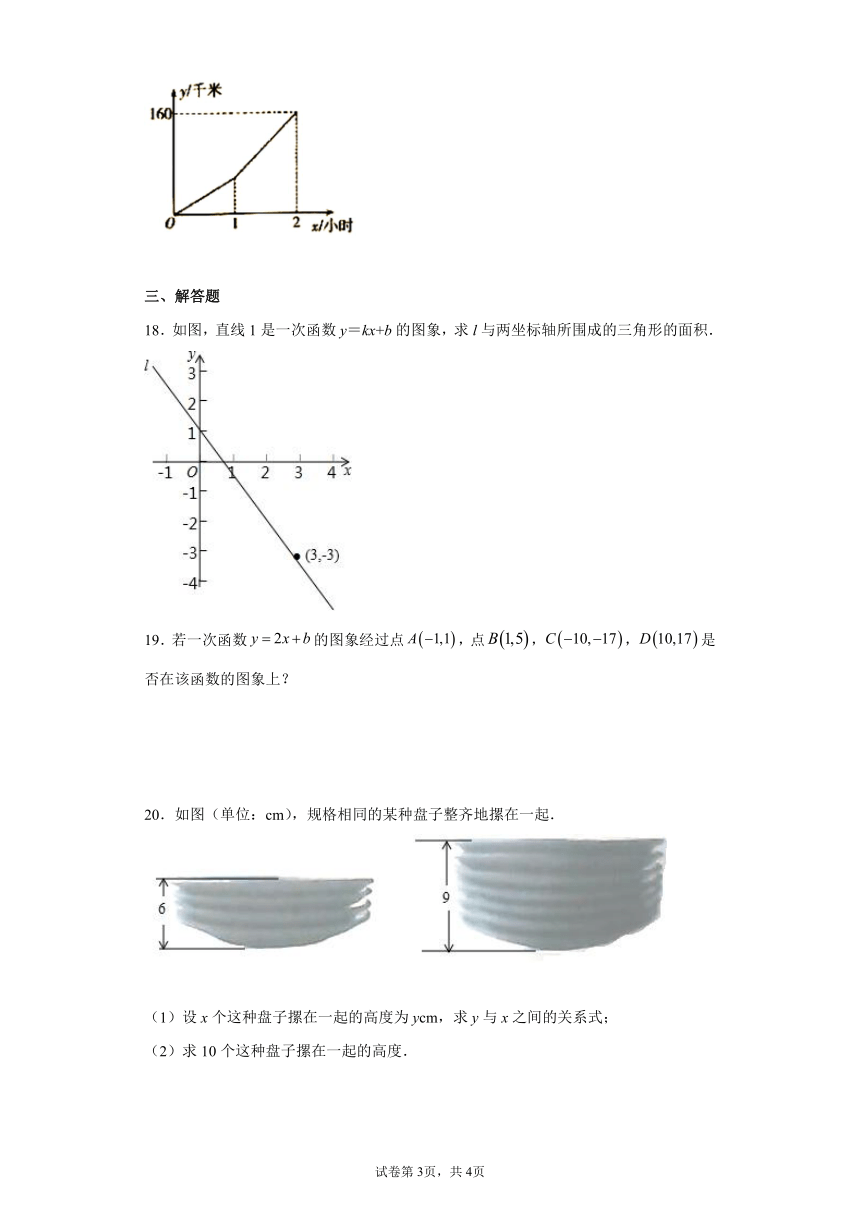
17.一辆汽车在行驶过程中,路程(千米)与时间(小时)之间的函数关系如图所示.当时,关于的函数解析式为,那么当时,关于的函数解析式为________.
三、解答题
18.如图,直线1是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.
19.若一次函数的图象经过点,点,,是否在该函数的图象上?
20.如图(单位:cm),规格相同的某种盘子整齐地摞在一起.
(1)设x个这种盘子摞在一起的高度为ycm,求y与x之间的关系式;
(2)求10个这种盘子摞在一起的高度.
21.已知一次函数的图象经过,两点.
(1)求这个一次函数的解析式;
(2)设图象与x轴、y轴交点分别是A、B,求点A、B的坐标;
(3)求此函数图象与x轴、y轴所围成的三角形的面积.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
2.C
3.D
4.C
5.B
6.A
7.C
8.C
9.C
10.C
11.(,0) (0,-3) 一、三、四 增大
12.>
13.且
14.
15.
16.-2
17.
18.
∵由题意x=0,y=1;x=3,y=-3,
∴
解得:
∴
∴直线与坐标轴的交点分别为(0,1),(,0),
∴函数与两坐标轴围成三角形的面积= =.
19.
解:点代入一次函数可得,解得,
所以一次函数解析式为:,
当代入解得,当代入解得,当代入解得,
所以点与点在该函数图象上,点不在该函数图象上.
20.
(1)解:设解析式为y=kx+b
由题意得:
解得:
∴解析式为
(2) 把x=10代入
得=12(cm)
21.
解:(1)设一次函数的解析式为,
由题意得:,
解得,
∴一次函数的解析式为:;
(2)令x=0,则y=1,
∴B(0,1),
令y=0,则,解得,
∴A(,0);
(3)∵A(,0),B(0,1),
∴,,
∴.答案第1页,共2页
答案第1页,共2页
2021-2022学年人教版八年级数学下册
一、单选题
1.下列一次函数中,y随x增大而增大的有( )
①;②;③;④;⑤.
A.①②③ B.①②⑤ C.①③⑤ D.①④⑤
2.函数的图象过点( ).
A. B. C. D.
3.直线与x轴的交点是,则k的值是( )
A.3 B.2 C. D.
4.一次函数(,为常数)的图象如图所示,则的取值范围是( )
A., B.,
C., D.,
5.下列图象中,以方程﹣2x+y﹣2=0的解为坐标的点组成的图象是( )
A. B. C. D.
6.要从直线得到直线,就要把直线( )
A.向上平移个单位 B.向下平移个单位
C.向左平移个单位 D.向右平移个单位
7.一次函数的图象与两坐标轴交于点A、B,则的面积等于( ).
A.18 B.12 C.9 D.6
8.一次函数的图象不经过( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知直线与直线平行,且直线l经过第二,三、四象限,则b的取值范围为( )
A. B. C. D.
10.某一次函数的图象经过点(,2),且函数的值随自变量x的增大而减小,则下列函数符合条件的是( )
A.y=4x+6 B.y=-x C.y=-x+1 D.y=-3x+5
二、填空题
11.直线与x轴交点坐标为_______,与y轴交点坐标为_______,图象经过_______象限,y随x的增大而_______.
12.直线经过点和点,若,则_____.
13.若一次函数的图象与y轴的交点在x轴的下方,则m的取值范围是_______.
14.直线平行于直线,且过点,则其解析式为________.
15.如图,直线是一次函数的图象,填空:
(1)当时,______;
(2)当时,______.
16.已知一次函数y=2x-a与y=3x+b的图象交于轴上原点外的一点,则=________.
17.一辆汽车在行驶过程中,路程(千米)与时间(小时)之间的函数关系如图所示.当时,关于的函数解析式为,那么当时,关于的函数解析式为________.
三、解答题
18.如图,直线1是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.
19.若一次函数的图象经过点,点,,是否在该函数的图象上?
20.如图(单位:cm),规格相同的某种盘子整齐地摞在一起.
(1)设x个这种盘子摞在一起的高度为ycm,求y与x之间的关系式;
(2)求10个这种盘子摞在一起的高度.
21.已知一次函数的图象经过,两点.
(1)求这个一次函数的解析式;
(2)设图象与x轴、y轴交点分别是A、B,求点A、B的坐标;
(3)求此函数图象与x轴、y轴所围成的三角形的面积.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
2.C
3.D
4.C
5.B
6.A
7.C
8.C
9.C
10.C
11.(,0) (0,-3) 一、三、四 增大
12.>
13.且
14.
15.
16.-2
17.
18.
∵由题意x=0,y=1;x=3,y=-3,
∴
解得:
∴
∴直线与坐标轴的交点分别为(0,1),(,0),
∴函数与两坐标轴围成三角形的面积= =.
19.
解:点代入一次函数可得,解得,
所以一次函数解析式为:,
当代入解得,当代入解得,当代入解得,
所以点与点在该函数图象上,点不在该函数图象上.
20.
(1)解:设解析式为y=kx+b
由题意得:
解得:
∴解析式为
(2) 把x=10代入
得=12(cm)
21.
解:(1)设一次函数的解析式为,
由题意得:,
解得,
∴一次函数的解析式为:;
(2)令x=0,则y=1,
∴B(0,1),
令y=0,则,解得,
∴A(,0);
(3)∵A(,0),B(0,1),
∴,,
∴.答案第1页,共2页
答案第1页,共2页
