2021——2022学年度人教版七年级数学下册5.2平行线及其判定 课后练习(Word版含答案)
文档属性
| 名称 | 2021——2022学年度人教版七年级数学下册5.2平行线及其判定 课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 252.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 19:59:38 | ||
图片预览


文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线5.2平行线及其判定 课后练习
一、选择题
1.已知直线,在同一平面内,给定一点,过点作直线的平行线,可作平行线的条数有( )
A.0条 B.1条 C.0条或1条 D.无数条
2.下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
3.如图,下列判断正确的是:( )
A.若∠1=∠2,则AD∥BC B.若∠1=∠2,则AB∥CD
C.若∠A=∠3,则AD∥BC D.若∠3+∠DAB=180° ,则AB∥CD
4.下列说法①两直线被第三条直线所截,同旁内角互补;②垂直于同一条直线的两条直线互相平行;③对顶角相等;④若∠A的两边和∠B的两边分别平行,且∠A比∠B的2倍少27°,则∠A的度数为69°,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
6.如图,下列条件中,能判断AB//CD的是( )
A.∠BAC=∠ACD B.∠1=∠2 C.∠3=∠4 D.∠BAD=∠BCD
7.如图所示,已知直线BF、CD相交于点O,,下面判定两条直线平行正确的是( )
A.当时,AB//CD B.当时,BC//DE C.当时,CD//EF D.当时,BF//DE
8.如图,点在的延长线上,则下列条件中,不能判定的是( )
A. B.
C. D.
9.如图所示,直线、被直线所截,下列条件不能使的是( )
A. B. C. D.
10.如图,给出下列四个条件:① ∠BAC=∠DCA;② ∠DAC=∠BCA;③ ∠ABD=∠CDB;④ ∠ADB=∠CBD,其中能使 AD∥BC的条件是( )
A.①② B.③④ C.②④ D.①③④
二、填空题
11.四条直线a、b、c、d互不重合,如果a∥b、b∥c、c∥d,那么直线a、d的位置关系为__________.
12.平面内三条直线a、b、c,若a⊥b,b⊥c,则a _______ c(填位置关系).
13.如图,直线a、b都与直线c相交,给出下列条件:① =;② +=;③=;④+=,其中能判断a∥b的条件是:______.(把你认为正确的序号全部填在空格内)
14.如图,在Rt△ABC中,∠B=90°,∠ACB=59°,EF//GH,若∠1=58°,则∠2=_____°.
15.已知,如图,要使得AB∥CD,你认为应该添加的一个条件是________
三、解答题
16.如图,已知∠1=∠2,∠MAE=45°,∠FEG=15°,∠NCE=75°。EG平分∠AEC.
求证:AB∥EF∥CD。
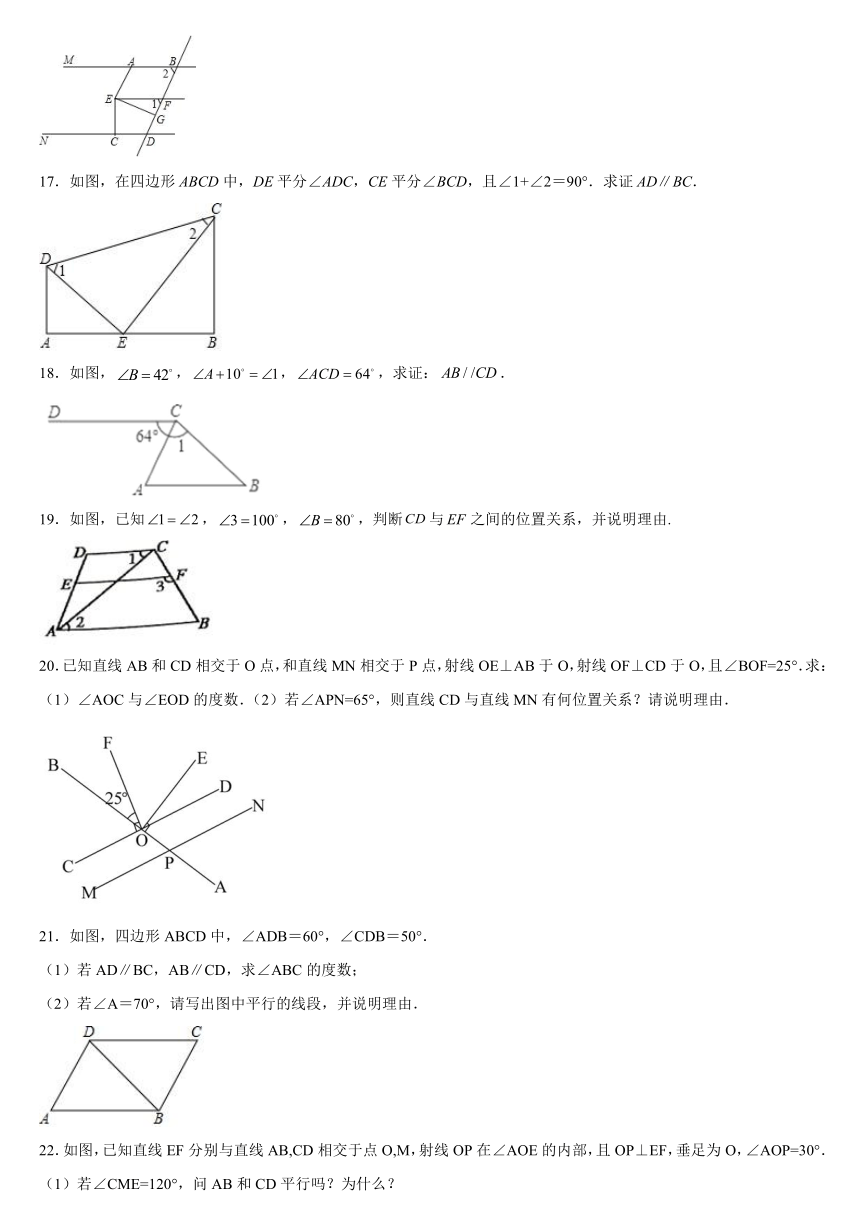
17.如图,在四边形ABCD中,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°.求证AD∥BC.
18.如图,,,,求证:.
19.如图,已知,,,判断与之间的位置关系,并说明理由.
20.已知直线AB和CD相交于O点,和直线MN相交于P点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°.求:(1)∠AOC与∠EOD的度数.(2)若∠APN=65°,则直线CD与直线MN有何位置关系?请说明理由.
21.如图,四边形ABCD中,∠ADB=60°,∠CDB=50°.
(1)若AD∥BC,AB∥CD,求∠ABC的度数;
(2)若∠A=70°,请写出图中平行的线段,并说明理由.
22.如图,已知直线EF分别与直线AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为O,∠AOP=30°.
(1)若∠CME=120°,问AB和CD平行吗?为什么?
(2)若直线AB∥CD,求∠EMD的度数.
23.已知,如图AO和BD相交于点O,E是CD上一点,F是OD上一点,EF∥OC,∠1=∠A
(1)试判断AB和CD的位置关系,并说明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度数.
【参考答案】
1.C 2.A 3.B 4.A 5.B 6.A 7.D 8.C 9.A 10.C
11.a∥d
12.平行
13.①④
14.27
∠ECD=∠A(答案不唯一).
16.证明:∵∠1=∠2,
∴AB∥EF(同位角相等,两直线平行),
∴∠MAE=∠AEF=45°,
∵∠FEG=15°,
∴∠AEG=60°,
∴∠GEC=60°,
∴∠FEC=∠FEG+∠GEC=75°,
∵∠NCE=75°,
∴∠FEC=∠ECN,
∴EF∥CD,
∴AB∥EF∥CD.
17.∵DE平分∠ADC,CE平分∠BCD,
∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,
∴∠ADC+∠BCD=2(∠1+∠2)=180°,
∴AD∥BC.
18.证明:在中,,,
∴,
又∵,
∵,
解得:.
∴,
∴(内错角相等,两直线平行).
19.解:,理由如下:
因为,
所以,
又因为,,
所以,
所以,
所以.
20.解:(1)∵OF⊥CD于O,且∠BOF=25°,
∴,
∴;
∴
∵OE⊥AB于O,
∴;
(2),理由如下,
∵,∠APN=65°,
∴(同位角相等,两直线平行).
21.解:(1)∵∠ADB=60°,∠CDB=50°,
∴∠ADC=110°
∵AD∥BC,
∴∠A=70°,
∵AB∥CD,
∴∠ABC=110°;
(2)AB∥CD.理由如下:
∵∠ADB=60°,∠A=70°,
∴∠ABD=50°,
∴∠CDB=∠ABD=50°,
∴AB∥CD.
22.(1)结论:AB∥CD.
理由:∵OP⊥OE,
∴∠POE=90°,
∵∠AOP=30°,
∴∠AOE=120°,
∵∠AME=120°,
∴∠AOE=∠CME,
∴AB∥CD.
(2)∵AB∥CD,
∴∠EMD=∠EOB,
∵∠EOB=180°-∠1OE=60°,
∴∠EMD=60°.
23.(1)AB//CD,
理由如下:
∵OC//EF,
∴∠1=∠C,
又∵∠1=∠A,
∴∠1=∠C,
∴AB//DC;
(2)∵∠1=65°,∠1=∠A,
∴∠A=65°,
又∵∠B=50°,
∴∠AOB=180o-(∠A+∠B)=65o.
一、选择题
1.已知直线,在同一平面内,给定一点,过点作直线的平行线,可作平行线的条数有( )
A.0条 B.1条 C.0条或1条 D.无数条
2.下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
3.如图,下列判断正确的是:( )
A.若∠1=∠2,则AD∥BC B.若∠1=∠2,则AB∥CD
C.若∠A=∠3,则AD∥BC D.若∠3+∠DAB=180° ,则AB∥CD
4.下列说法①两直线被第三条直线所截,同旁内角互补;②垂直于同一条直线的两条直线互相平行;③对顶角相等;④若∠A的两边和∠B的两边分别平行,且∠A比∠B的2倍少27°,则∠A的度数为69°,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
6.如图,下列条件中,能判断AB//CD的是( )
A.∠BAC=∠ACD B.∠1=∠2 C.∠3=∠4 D.∠BAD=∠BCD
7.如图所示,已知直线BF、CD相交于点O,,下面判定两条直线平行正确的是( )
A.当时,AB//CD B.当时,BC//DE C.当时,CD//EF D.当时,BF//DE
8.如图,点在的延长线上,则下列条件中,不能判定的是( )
A. B.
C. D.
9.如图所示,直线、被直线所截,下列条件不能使的是( )
A. B. C. D.
10.如图,给出下列四个条件:① ∠BAC=∠DCA;② ∠DAC=∠BCA;③ ∠ABD=∠CDB;④ ∠ADB=∠CBD,其中能使 AD∥BC的条件是( )
A.①② B.③④ C.②④ D.①③④
二、填空题
11.四条直线a、b、c、d互不重合,如果a∥b、b∥c、c∥d,那么直线a、d的位置关系为__________.
12.平面内三条直线a、b、c,若a⊥b,b⊥c,则a _______ c(填位置关系).
13.如图,直线a、b都与直线c相交,给出下列条件:① =;② +=;③=;④+=,其中能判断a∥b的条件是:______.(把你认为正确的序号全部填在空格内)
14.如图,在Rt△ABC中,∠B=90°,∠ACB=59°,EF//GH,若∠1=58°,则∠2=_____°.
15.已知,如图,要使得AB∥CD,你认为应该添加的一个条件是________
三、解答题
16.如图,已知∠1=∠2,∠MAE=45°,∠FEG=15°,∠NCE=75°。EG平分∠AEC.
求证:AB∥EF∥CD。
17.如图,在四边形ABCD中,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°.求证AD∥BC.
18.如图,,,,求证:.
19.如图,已知,,,判断与之间的位置关系,并说明理由.
20.已知直线AB和CD相交于O点,和直线MN相交于P点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°.求:(1)∠AOC与∠EOD的度数.(2)若∠APN=65°,则直线CD与直线MN有何位置关系?请说明理由.
21.如图,四边形ABCD中,∠ADB=60°,∠CDB=50°.
(1)若AD∥BC,AB∥CD,求∠ABC的度数;
(2)若∠A=70°,请写出图中平行的线段,并说明理由.
22.如图,已知直线EF分别与直线AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为O,∠AOP=30°.
(1)若∠CME=120°,问AB和CD平行吗?为什么?
(2)若直线AB∥CD,求∠EMD的度数.
23.已知,如图AO和BD相交于点O,E是CD上一点,F是OD上一点,EF∥OC,∠1=∠A
(1)试判断AB和CD的位置关系,并说明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度数.
【参考答案】
1.C 2.A 3.B 4.A 5.B 6.A 7.D 8.C 9.A 10.C
11.a∥d
12.平行
13.①④
14.27
∠ECD=∠A(答案不唯一).
16.证明:∵∠1=∠2,
∴AB∥EF(同位角相等,两直线平行),
∴∠MAE=∠AEF=45°,
∵∠FEG=15°,
∴∠AEG=60°,
∴∠GEC=60°,
∴∠FEC=∠FEG+∠GEC=75°,
∵∠NCE=75°,
∴∠FEC=∠ECN,
∴EF∥CD,
∴AB∥EF∥CD.
17.∵DE平分∠ADC,CE平分∠BCD,
∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,
∴∠ADC+∠BCD=2(∠1+∠2)=180°,
∴AD∥BC.
18.证明:在中,,,
∴,
又∵,
∵,
解得:.
∴,
∴(内错角相等,两直线平行).
19.解:,理由如下:
因为,
所以,
又因为,,
所以,
所以,
所以.
20.解:(1)∵OF⊥CD于O,且∠BOF=25°,
∴,
∴;
∴
∵OE⊥AB于O,
∴;
(2),理由如下,
∵,∠APN=65°,
∴(同位角相等,两直线平行).
21.解:(1)∵∠ADB=60°,∠CDB=50°,
∴∠ADC=110°
∵AD∥BC,
∴∠A=70°,
∵AB∥CD,
∴∠ABC=110°;
(2)AB∥CD.理由如下:
∵∠ADB=60°,∠A=70°,
∴∠ABD=50°,
∴∠CDB=∠ABD=50°,
∴AB∥CD.
22.(1)结论:AB∥CD.
理由:∵OP⊥OE,
∴∠POE=90°,
∵∠AOP=30°,
∴∠AOE=120°,
∵∠AME=120°,
∴∠AOE=∠CME,
∴AB∥CD.
(2)∵AB∥CD,
∴∠EMD=∠EOB,
∵∠EOB=180°-∠1OE=60°,
∴∠EMD=60°.
23.(1)AB//CD,
理由如下:
∵OC//EF,
∴∠1=∠C,
又∵∠1=∠A,
∴∠1=∠C,
∴AB//DC;
(2)∵∠1=65°,∠1=∠A,
∴∠A=65°,
又∵∠B=50°,
∴∠AOB=180o-(∠A+∠B)=65o.
