2021-2022学年人教版数学八年级下册16.3.1二次根式的加减 复习讲义 学案(无答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册16.3.1二次根式的加减 复习讲义 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 76.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 00:00:00 | ||
图片预览

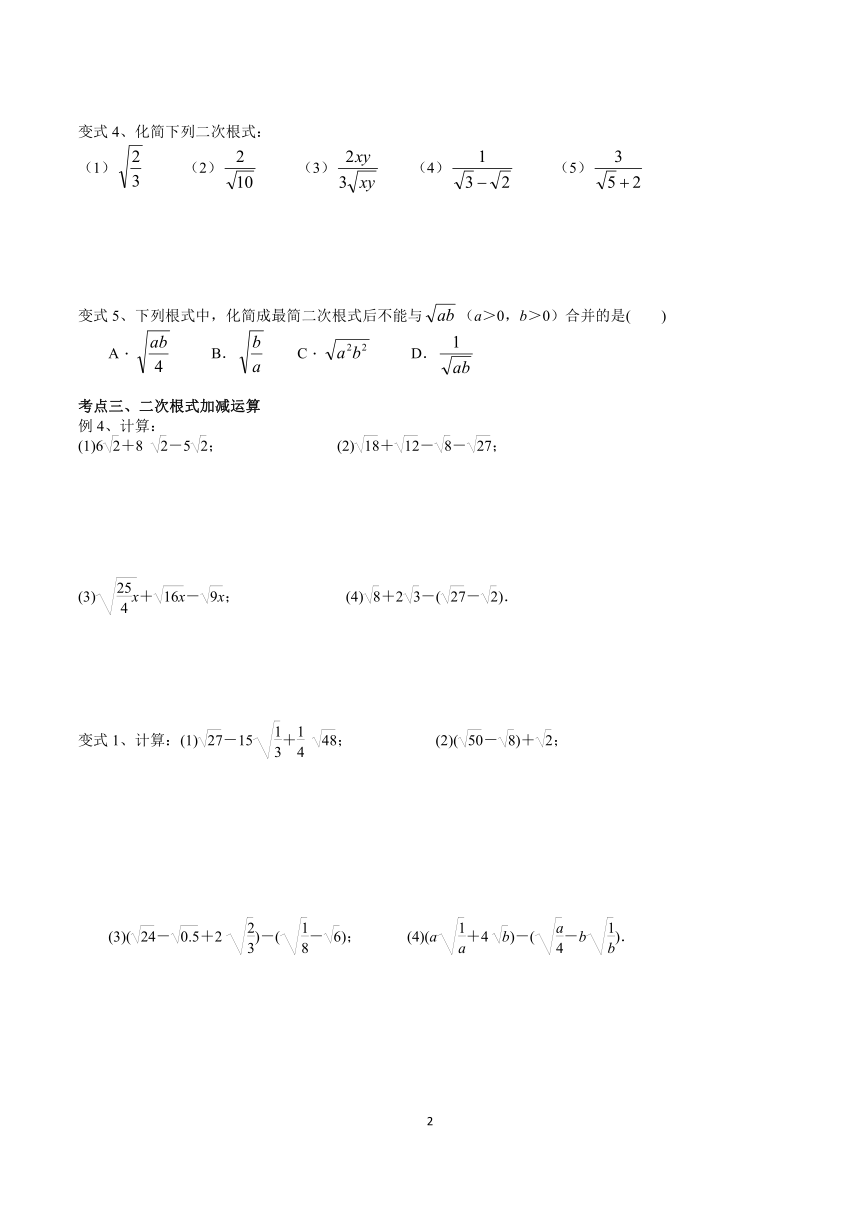
文档简介
16.3.1二次根式的加减
知识点二、二次根式加减运算法则
1、二次根式加减运算法则:在二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
2、二次根式的加减法运算步骤:
(1)化成最简二次根式;
(2)找出被开方数相同的二次根式
(3)合并被开方数相同的二次根式——将系数相加减仍作为系数根指数与被开方数保持不变。
点拨 二次根式的加减与整式的加减相比,可将被开方数相同的二次根式看作整式加减中的同类项进行合并。另外,有理数的加法交换律、结合律,乘法交换律、结合律,乘法对加法的分配律,以及多项式的乘法公式,都适用于二次根式的运算。
知识点二、二次根式分母有理化
一般常见的互为有理化因式有如下几类:
①与; ②与;
③与; ④与.
说明:利用有理化因式的特点可以将分母有理化.
考点一、二次根式的化简
例1、下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
例2、已知最简二次根式与能合并成一项,则x的值是( )
A.5 B.4 C.3 D.2
例3、化简下列二次根式:
(1) (2) (3) (4) (5)
变式1、下列各组二次根式中,是同类二次根式的一组是( )
A.与 B.与 C.与 D.与
变式2、在下列二次根式中:
2 , ,,4 , .
(1)能与合并的是______________;
(2)能与合并的是______________.
变式3、若最简二次根式与可以合并,则a的值为__________.
变式4、化简下列二次根式:
(1) (2) (3) (4) (5)
变式5、下列根式中,化简成最简二次根式后不能与(a>0,b>0)合并的是( )
A. B. C. D.
考点三、二次根式加减运算
例4、计算:
(1)6+8 -5; (2)+--;
(3)+-; (4)+2-(-).
变式1、计算:(1)-15+ ; (2)(-)+;
(3)(-+2 )-(-); (4)(a+4 )-(-b).
变式2、计算+2-的结果是( )
A. B.1 C.5 D.6 -
变式3、计算:-+=________.
变式4、已知a,b,c满足=0.
(1)求a,b,c的值
(2)以a,b,c为边长能否构成三角形,若能构成三角形,请说明理由并求出其周长;若不能,请说明理由。
变式5、先化简,再求值:(+)÷,其中x=+2,y=-2.
1、下列各式中,正确的是 ( )
A. += B.2+=2 C.3-=3 D. -=
2、下列计算正确的是( )
A.4 -3 =1 B.+= C.2 = D.3+2 =5
3、计算-9的结果是( )
A.- B. C.- D.
4、式子x+6x-4x的值一定是( )
A.正数 B.非正数 C.非负数 D.负数
5、与最简二次根式5 可以合并,则a=________.
6、若等腰三角形两边的长分别是2 ,3 ,则这个三角形的周长是____________.
7、计算-的结果是 。
8、计算:+-2=________.
9、计算:
(1)(-4)-(3-4); (2)
(3)2 (4)
10、一个三角形的三边长分别为5 , ,x.
(1)求它的周长(结果化为最简二次根式);
(2)请你给出一个适当的x的值,使它的周长为有理数,并求出此时三角形的周长.
11、先化简,再求值:,其中x=.
知识点二、二次根式加减运算法则
1、二次根式加减运算法则:在二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
2、二次根式的加减法运算步骤:
(1)化成最简二次根式;
(2)找出被开方数相同的二次根式
(3)合并被开方数相同的二次根式——将系数相加减仍作为系数根指数与被开方数保持不变。
点拨 二次根式的加减与整式的加减相比,可将被开方数相同的二次根式看作整式加减中的同类项进行合并。另外,有理数的加法交换律、结合律,乘法交换律、结合律,乘法对加法的分配律,以及多项式的乘法公式,都适用于二次根式的运算。
知识点二、二次根式分母有理化
一般常见的互为有理化因式有如下几类:
①与; ②与;
③与; ④与.
说明:利用有理化因式的特点可以将分母有理化.
考点一、二次根式的化简
例1、下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
例2、已知最简二次根式与能合并成一项,则x的值是( )
A.5 B.4 C.3 D.2
例3、化简下列二次根式:
(1) (2) (3) (4) (5)
变式1、下列各组二次根式中,是同类二次根式的一组是( )
A.与 B.与 C.与 D.与
变式2、在下列二次根式中:
2 , ,,4 , .
(1)能与合并的是______________;
(2)能与合并的是______________.
变式3、若最简二次根式与可以合并,则a的值为__________.
变式4、化简下列二次根式:
(1) (2) (3) (4) (5)
变式5、下列根式中,化简成最简二次根式后不能与(a>0,b>0)合并的是( )
A. B. C. D.
考点三、二次根式加减运算
例4、计算:
(1)6+8 -5; (2)+--;
(3)+-; (4)+2-(-).
变式1、计算:(1)-15+ ; (2)(-)+;
(3)(-+2 )-(-); (4)(a+4 )-(-b).
变式2、计算+2-的结果是( )
A. B.1 C.5 D.6 -
变式3、计算:-+=________.
变式4、已知a,b,c满足=0.
(1)求a,b,c的值
(2)以a,b,c为边长能否构成三角形,若能构成三角形,请说明理由并求出其周长;若不能,请说明理由。
变式5、先化简,再求值:(+)÷,其中x=+2,y=-2.
1、下列各式中,正确的是 ( )
A. += B.2+=2 C.3-=3 D. -=
2、下列计算正确的是( )
A.4 -3 =1 B.+= C.2 = D.3+2 =5
3、计算-9的结果是( )
A.- B. C.- D.
4、式子x+6x-4x的值一定是( )
A.正数 B.非正数 C.非负数 D.负数
5、与最简二次根式5 可以合并,则a=________.
6、若等腰三角形两边的长分别是2 ,3 ,则这个三角形的周长是____________.
7、计算-的结果是 。
8、计算:+-2=________.
9、计算:
(1)(-4)-(3-4); (2)
(3)2 (4)
10、一个三角形的三边长分别为5 , ,x.
(1)求它的周长(结果化为最简二次根式);
(2)请你给出一个适当的x的值,使它的周长为有理数,并求出此时三角形的周长.
11、先化简,再求值:,其中x=.
