明达中学高二下入学考试模拟试卷1(Word含答案)
文档属性
| 名称 | 明达中学高二下入学考试模拟试卷1(Word含答案) | 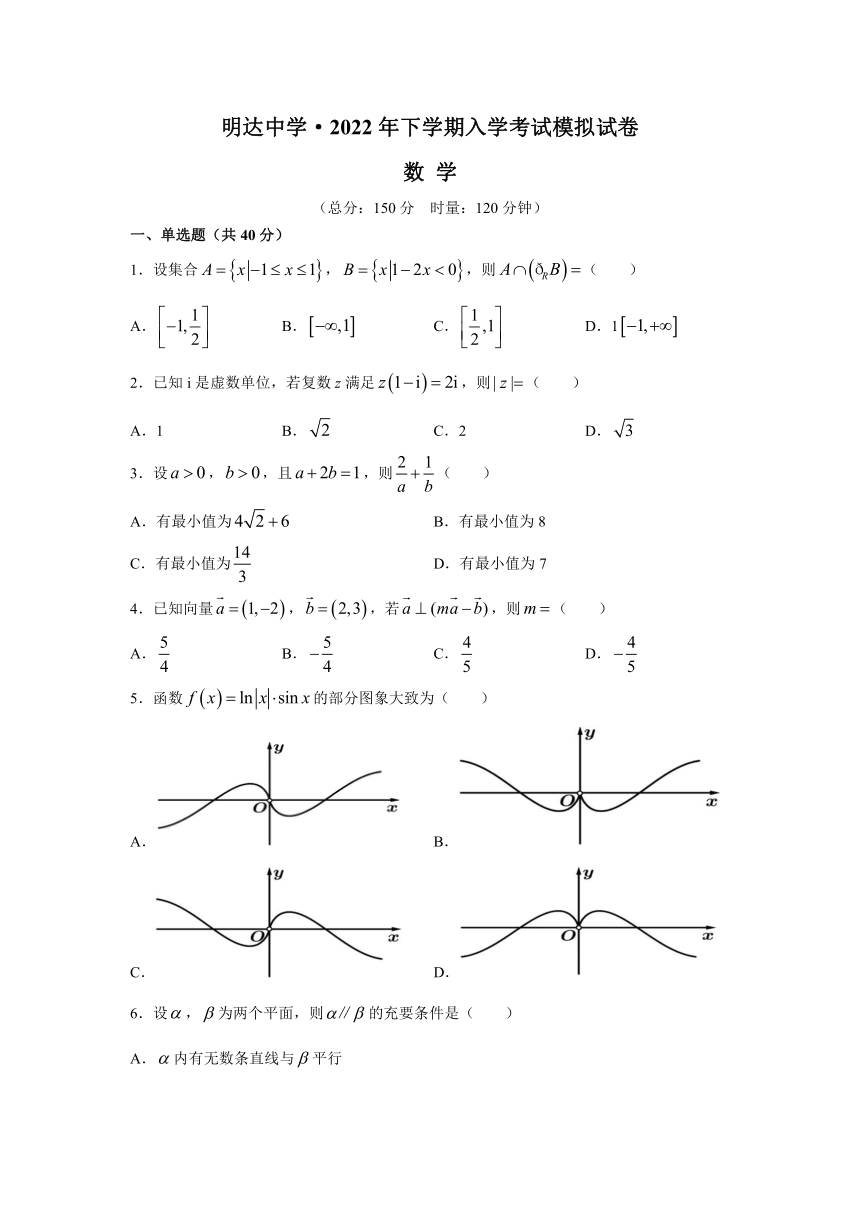 | |
| 格式 | zip | ||
| 文件大小 | 779.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 22:03:37 | ||
图片预览




文档简介
明达中学·2022年下学期入学考试模拟试卷
数 学
(总分:150分 时量:120分钟)
一、单选题(共40分)
1.设集合,,则( )
A. B. C. D.1
2.已知i是虚数单位,若复数z满足,则( )
A.1 B. C.2 D.
3.设,,且,则( )
A.有最小值为 B.有最小值为8
C.有最小值为 D.有最小值为7
4.已知向量,,若,则( )
A. B. C. D.
5.函数的部分图象大致为( )
A. B.
C. D.
6.设,为两个平面,则的充要条件是( )
A.内有无数条直线与平行
B.内有两条相交直线与平行
C.,平行于同一条直线
D.,垂直于同一平面
7.在区间上任取一个整数x,则满足的概率为( )
A. B. C. D.
8.在中,角A,B,C的对边分别为a,b,c,若,,则面积的最大值为( )
A.1 B. C.2 D.
二、多选题(共20分)
9.下列四个正方体图形中,A,B为正方体的两个顶点,M、N、P分别为其所在棱的中点,不能得出平面MNP的图形是( )
A. B. C. D.
10.某城市为促进家庭节约用电,计划制定阶梯电价,阶梯电价按年月均用电量从低到高分为一、二、三、四档,第一档电价的家庭约占10%,第二档电价的家庭约占40%,第三档电价的家庭约占30%,第四档电价的家庭约占20%.为确定各档之间的界限,从该市的家庭中抽查了部分家庭,调查了他们上一年度的年月均用电量(单位:千瓦时),由调查结果得下面的直方图.由此直方图可以做出的合理判断是( )
A.年月均用电量不超过80千瓦时的家庭属于第一档
B.年均用电量低于200千瓦时,且超过80千瓦时的家庭属于第二档
C.年月均用电量超过240千瓦时的家庭属于第四档
D.该市家庭的年月均用电量的平均数大于年月均用电量的中位数
11.已知函数,则关于x的方程的解可以为( )
A. B.0 C. D.
12.函数同时满足:①对于定义域上的任意x,恒有;②对于定义域上的任意x1,x2,当,恒有.则称函数为“理想函数”,下列三个函数中,是“理想函数”的有( )
A. B. C. D.
三、填空题(共20分)
13.已知幂函数在单调递减,则n的值为______.
14.已知x0是函数的零点,且,则______.
15.已知,则______.
16.如图,在边长为2的正方体中,点E,F分别为AD,AB的中点,则直线EF与平面BCD1所成角的大小为______.
四、解答题(共70分)
17.已知平行四边形ABCD中,,,,点E是线段BC的中点.
(I)求的值;
(II)若,且,求的值.
18.已知函数.
(1)求的最小正周期;
(2)求在区间上的最大值,并求出此时对应的x的值.
19.在中,角A,B,C所对的边分别为a,b,c,且.
(1)求A;
(2)若,求面积的最大值.
20.如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)80~90这一组的频数 频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数 众数 中位数.
(3)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
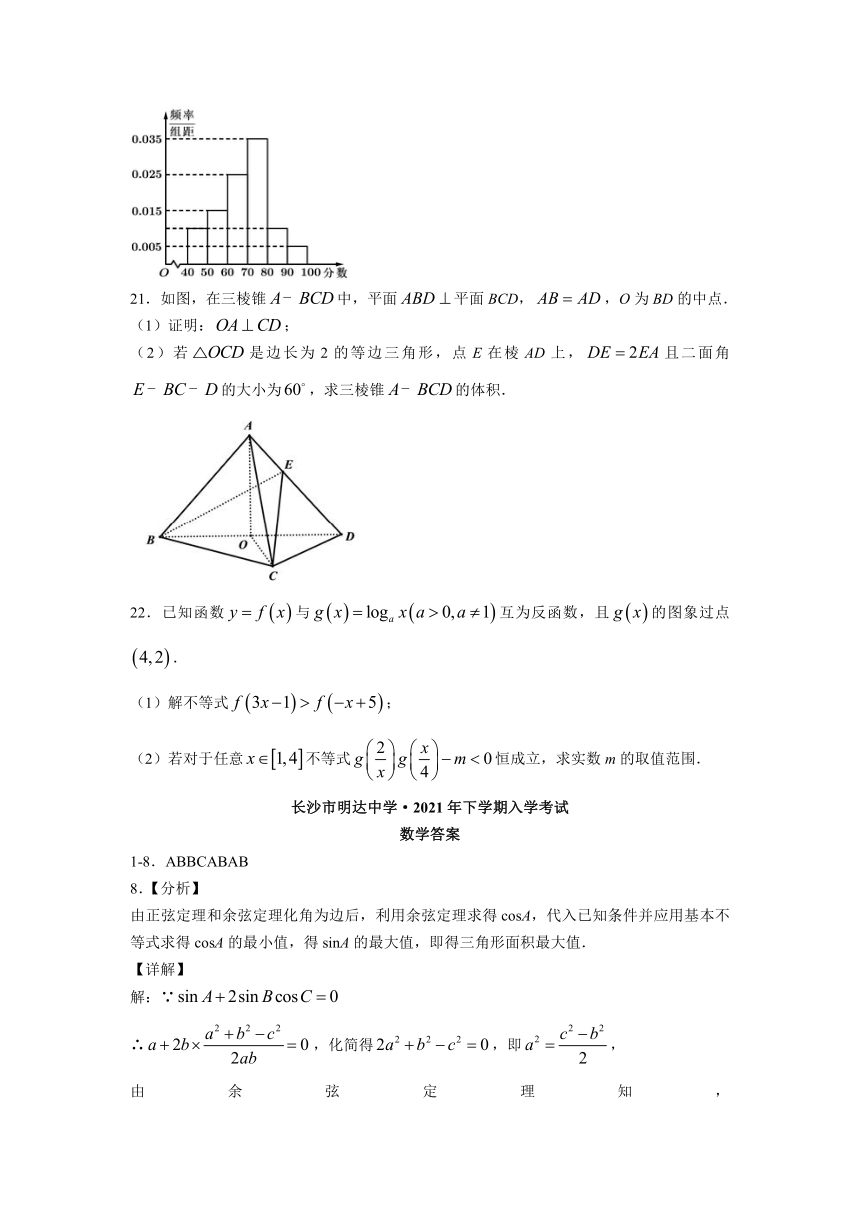
21.如图,在三棱锥中,平面平面BCD,,O为BD的中点.
(1)证明:;
(2)若是边长为2的等边三角形,点E在棱AD上,且二面角的大小为,求三棱锥的体积.
22.已知函数与互为反函数,且的图象过点.
(1)解不等式;
(2)若对于任意不等式恒成立,求实数m的取值范围.
长沙市明达中学·2021年下学期入学考试
数学答案
1-8.ABBCABAB
8.【分析】
由正弦定理和余弦定理化角为边后,利用余弦定理求得cosA,代入已知条件并应用基本不等式求得cosA的最小值,得sinA的最大值,即得三角形面积最大值.
【详解】
解:∵
∴,化简得,即,
由余弦定理知,,
∴,
∴,
的面积.
故选:B.
9.BC 10.ACD 11.AD 12.AC
13.1 14.3 15. 16.
17.(I)4;(II).
【分析】
(I)建立坐标系,利用坐标求解数量积,或者利用数量积的定义求解;
(II)求出向量,的坐标,结合向量垂直的坐标表示可求的值,或者位置关系求解.
【详解】
法1:(I)
以A点为坐标原点,AB所在直线为x轴建立如图所示的平面直角坐标系,则
,,,,,
,,
∴;
(II),
∵,∴,
∴.
法2:
(I);
(II),∴
∵,,∴F与B重合,∴.
18.(1);(2)当时,取得最大值.
【分析】
(1)利用正余弦的二倍角公式以及辅助角公式化简,再由正弦函数的周期公式即可求解;
(2)由x的范围求出的范围,结合正弦函数的性质即可求解.
【详解】
(1)
所以的最小正周期为
(2)因为,所以,
所以当即时, 取得最大值为,
此时,
所以当时,取得最大值.
19.(1);(2).
【分析】
(1)利用正弦定理将转化为,然后利用三角恒等变换公式化简可求出角A;
(2)由余弦定理结合基本不等式可求得面积的最大值.
【详解】
(1)由正弦定理得,
又∵,
∴,又∵,∴,∴,
故在中,;
(2)由余弦定理得:,
∴,
∴,当且仅当时取等号,
∴面积.当且仅当时取等号,
故面积的最大值为.
20.(1)4,0.1;(2)68.5,75,70;(3).
【分析】
(1)根据频率分步直方图的意义,计算可得40~50、50~60、60~70、70~80、90~100这5组的频率,由频率的性质可得80~90这一组的频率,进而由频率、频数的关系,计算可得答案;
(2)根据频率分步直方图中计算平均数、众数、中位数的方法,计算可得答案;
(3)记“取出的2人在同一分数段”为事件E,计算可得80~90之间与90~100之间的人数,并设为a、b、c、d,和A、B,列举可得从中取出2人的情况,可得其情况数目与取出的2人在同一分数段的情况数目,由等可能事件的概率公式,计算可得答案.
【详解】
(1)根据题意,40~50的这一组的频率为,
50~60的这一组的频率为,
60~70的这一组的频率为,
70~80的这一组的频率为,
90~100的这一组的频率为,
则80~90这一组的频率为,
其频数为;
(2)这次竞赛的平均数为,
70~80一组的频率最大,人数最多,则众数为75,
70分左右两侧的频率均为0.5,则中位数为70;
(3)记“取出的2人在同一分数段”为事件E,
因为80~90之间的人数为,设为a、b、c、d,
90~100之间有人,设为A B,
从这6人中选出2人,有
、、、、、、、
、、、、、、、
,共15个基本事件,
其中事件E包括、、、、、、,共7个基本事件,
则.
21.(1)证明见解析;(2)4.
【分析】
(1)由等腰三角形的性质可得,而平面平面BCD,则由面面垂直的性质定理可得面BCD,再由线面垂直的性质定理可得,
(2)过点E作交BD于N.过点N作交BC于点M,连接ME,则可得面BCD,由可得三角形BCD为直角三角形,从而可得为所求的二面角的平面角,所以由,可得,再结合平行关系和是边长为2的等边三角形,可求出三棱锥的体积.
【详解】
(1)∵,O为BD中点,∴,
Q 面ABD,面面BCD,且面面,
∴面BCD,∵面BCD,∴.
(2)过点E作交BD于N.过点N作交BC于点M,连接ME,因为且由(1)知面BCD,
所以面BCD, ∵面BCD,∴
在△BCD中,∵,∴,
Q ,∴,∴面MNE
∴
∴为所求的二面角的平面角
∴,∴
∵,,∴,
Q ,∴
∵,∴.∴,∴.
∴
∴.
22.(1);(2).
【分析】
利用已知条件得到a的值,进而得到的解析式,再利用函数的图象关于x轴对称,可得的解析式;
(1)先利用对数函数的单调性,列出不等式组求解即可;
(2)对于任意恒成立等价于,令,,利用二次函数求解即可.
【详解】
∵,∴,,∴
由已知得,即.
(1)∵在上单调递减,∴,解得,
\x的取值范围为.
(2)∵,
∴对于任意恒成立等价于,
∵,
令,,则,
∴,当,
即,即时,,.
【点睛】
结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数,,
(1)若,,总有成立,故;
(2)若,,有成立,故;
(3)若,,有成立,故;
(4)若,,有,则的值域是值域的子集
数 学
(总分:150分 时量:120分钟)
一、单选题(共40分)
1.设集合,,则( )
A. B. C. D.1
2.已知i是虚数单位,若复数z满足,则( )
A.1 B. C.2 D.
3.设,,且,则( )
A.有最小值为 B.有最小值为8
C.有最小值为 D.有最小值为7
4.已知向量,,若,则( )
A. B. C. D.
5.函数的部分图象大致为( )
A. B.
C. D.
6.设,为两个平面,则的充要条件是( )
A.内有无数条直线与平行
B.内有两条相交直线与平行
C.,平行于同一条直线
D.,垂直于同一平面
7.在区间上任取一个整数x,则满足的概率为( )
A. B. C. D.
8.在中,角A,B,C的对边分别为a,b,c,若,,则面积的最大值为( )
A.1 B. C.2 D.
二、多选题(共20分)
9.下列四个正方体图形中,A,B为正方体的两个顶点,M、N、P分别为其所在棱的中点,不能得出平面MNP的图形是( )
A. B. C. D.
10.某城市为促进家庭节约用电,计划制定阶梯电价,阶梯电价按年月均用电量从低到高分为一、二、三、四档,第一档电价的家庭约占10%,第二档电价的家庭约占40%,第三档电价的家庭约占30%,第四档电价的家庭约占20%.为确定各档之间的界限,从该市的家庭中抽查了部分家庭,调查了他们上一年度的年月均用电量(单位:千瓦时),由调查结果得下面的直方图.由此直方图可以做出的合理判断是( )
A.年月均用电量不超过80千瓦时的家庭属于第一档
B.年均用电量低于200千瓦时,且超过80千瓦时的家庭属于第二档
C.年月均用电量超过240千瓦时的家庭属于第四档
D.该市家庭的年月均用电量的平均数大于年月均用电量的中位数
11.已知函数,则关于x的方程的解可以为( )
A. B.0 C. D.
12.函数同时满足:①对于定义域上的任意x,恒有;②对于定义域上的任意x1,x2,当,恒有.则称函数为“理想函数”,下列三个函数中,是“理想函数”的有( )
A. B. C. D.
三、填空题(共20分)
13.已知幂函数在单调递减,则n的值为______.
14.已知x0是函数的零点,且,则______.
15.已知,则______.
16.如图,在边长为2的正方体中,点E,F分别为AD,AB的中点,则直线EF与平面BCD1所成角的大小为______.
四、解答题(共70分)
17.已知平行四边形ABCD中,,,,点E是线段BC的中点.
(I)求的值;
(II)若,且,求的值.
18.已知函数.
(1)求的最小正周期;
(2)求在区间上的最大值,并求出此时对应的x的值.
19.在中,角A,B,C所对的边分别为a,b,c,且.
(1)求A;
(2)若,求面积的最大值.
20.如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)80~90这一组的频数 频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数 众数 中位数.
(3)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
21.如图,在三棱锥中,平面平面BCD,,O为BD的中点.
(1)证明:;
(2)若是边长为2的等边三角形,点E在棱AD上,且二面角的大小为,求三棱锥的体积.
22.已知函数与互为反函数,且的图象过点.
(1)解不等式;
(2)若对于任意不等式恒成立,求实数m的取值范围.
长沙市明达中学·2021年下学期入学考试
数学答案
1-8.ABBCABAB
8.【分析】
由正弦定理和余弦定理化角为边后,利用余弦定理求得cosA,代入已知条件并应用基本不等式求得cosA的最小值,得sinA的最大值,即得三角形面积最大值.
【详解】
解:∵
∴,化简得,即,
由余弦定理知,,
∴,
∴,
的面积.
故选:B.
9.BC 10.ACD 11.AD 12.AC
13.1 14.3 15. 16.
17.(I)4;(II).
【分析】
(I)建立坐标系,利用坐标求解数量积,或者利用数量积的定义求解;
(II)求出向量,的坐标,结合向量垂直的坐标表示可求的值,或者位置关系求解.
【详解】
法1:(I)
以A点为坐标原点,AB所在直线为x轴建立如图所示的平面直角坐标系,则
,,,,,
,,
∴;
(II),
∵,∴,
∴.
法2:
(I);
(II),∴
∵,,∴F与B重合,∴.
18.(1);(2)当时,取得最大值.
【分析】
(1)利用正余弦的二倍角公式以及辅助角公式化简,再由正弦函数的周期公式即可求解;
(2)由x的范围求出的范围,结合正弦函数的性质即可求解.
【详解】
(1)
所以的最小正周期为
(2)因为,所以,
所以当即时, 取得最大值为,
此时,
所以当时,取得最大值.
19.(1);(2).
【分析】
(1)利用正弦定理将转化为,然后利用三角恒等变换公式化简可求出角A;
(2)由余弦定理结合基本不等式可求得面积的最大值.
【详解】
(1)由正弦定理得,
又∵,
∴,又∵,∴,∴,
故在中,;
(2)由余弦定理得:,
∴,
∴,当且仅当时取等号,
∴面积.当且仅当时取等号,
故面积的最大值为.
20.(1)4,0.1;(2)68.5,75,70;(3).
【分析】
(1)根据频率分步直方图的意义,计算可得40~50、50~60、60~70、70~80、90~100这5组的频率,由频率的性质可得80~90这一组的频率,进而由频率、频数的关系,计算可得答案;
(2)根据频率分步直方图中计算平均数、众数、中位数的方法,计算可得答案;
(3)记“取出的2人在同一分数段”为事件E,计算可得80~90之间与90~100之间的人数,并设为a、b、c、d,和A、B,列举可得从中取出2人的情况,可得其情况数目与取出的2人在同一分数段的情况数目,由等可能事件的概率公式,计算可得答案.
【详解】
(1)根据题意,40~50的这一组的频率为,
50~60的这一组的频率为,
60~70的这一组的频率为,
70~80的这一组的频率为,
90~100的这一组的频率为,
则80~90这一组的频率为,
其频数为;
(2)这次竞赛的平均数为,
70~80一组的频率最大,人数最多,则众数为75,
70分左右两侧的频率均为0.5,则中位数为70;
(3)记“取出的2人在同一分数段”为事件E,
因为80~90之间的人数为,设为a、b、c、d,
90~100之间有人,设为A B,
从这6人中选出2人,有
、、、、、、、
、、、、、、、
,共15个基本事件,
其中事件E包括、、、、、、,共7个基本事件,
则.
21.(1)证明见解析;(2)4.
【分析】
(1)由等腰三角形的性质可得,而平面平面BCD,则由面面垂直的性质定理可得面BCD,再由线面垂直的性质定理可得,
(2)过点E作交BD于N.过点N作交BC于点M,连接ME,则可得面BCD,由可得三角形BCD为直角三角形,从而可得为所求的二面角的平面角,所以由,可得,再结合平行关系和是边长为2的等边三角形,可求出三棱锥的体积.
【详解】
(1)∵,O为BD中点,∴,
Q 面ABD,面面BCD,且面面,
∴面BCD,∵面BCD,∴.
(2)过点E作交BD于N.过点N作交BC于点M,连接ME,因为且由(1)知面BCD,
所以面BCD, ∵面BCD,∴
在△BCD中,∵,∴,
Q ,∴,∴面MNE
∴
∴为所求的二面角的平面角
∴,∴
∵,,∴,
Q ,∴
∵,∴.∴,∴.
∴
∴.
22.(1);(2).
【分析】
利用已知条件得到a的值,进而得到的解析式,再利用函数的图象关于x轴对称,可得的解析式;
(1)先利用对数函数的单调性,列出不等式组求解即可;
(2)对于任意恒成立等价于,令,,利用二次函数求解即可.
【详解】
∵,∴,,∴
由已知得,即.
(1)∵在上单调递减,∴,解得,
\x的取值范围为.
(2)∵,
∴对于任意恒成立等价于,
∵,
令,,则,
∴,当,
即,即时,,.
【点睛】
结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数,,
(1)若,,总有成立,故;
(2)若,,有成立,故;
(3)若,,有成立,故;
(4)若,,有,则的值域是值域的子集
同课章节目录
