2021-2022学年人教版七年级数学下册5.2.2平行线的判定课后练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.2平行线的判定课后练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 242.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 15:58:56 | ||
图片预览

文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线 5.2.2 平行线的判定 课后练习
一、选择题
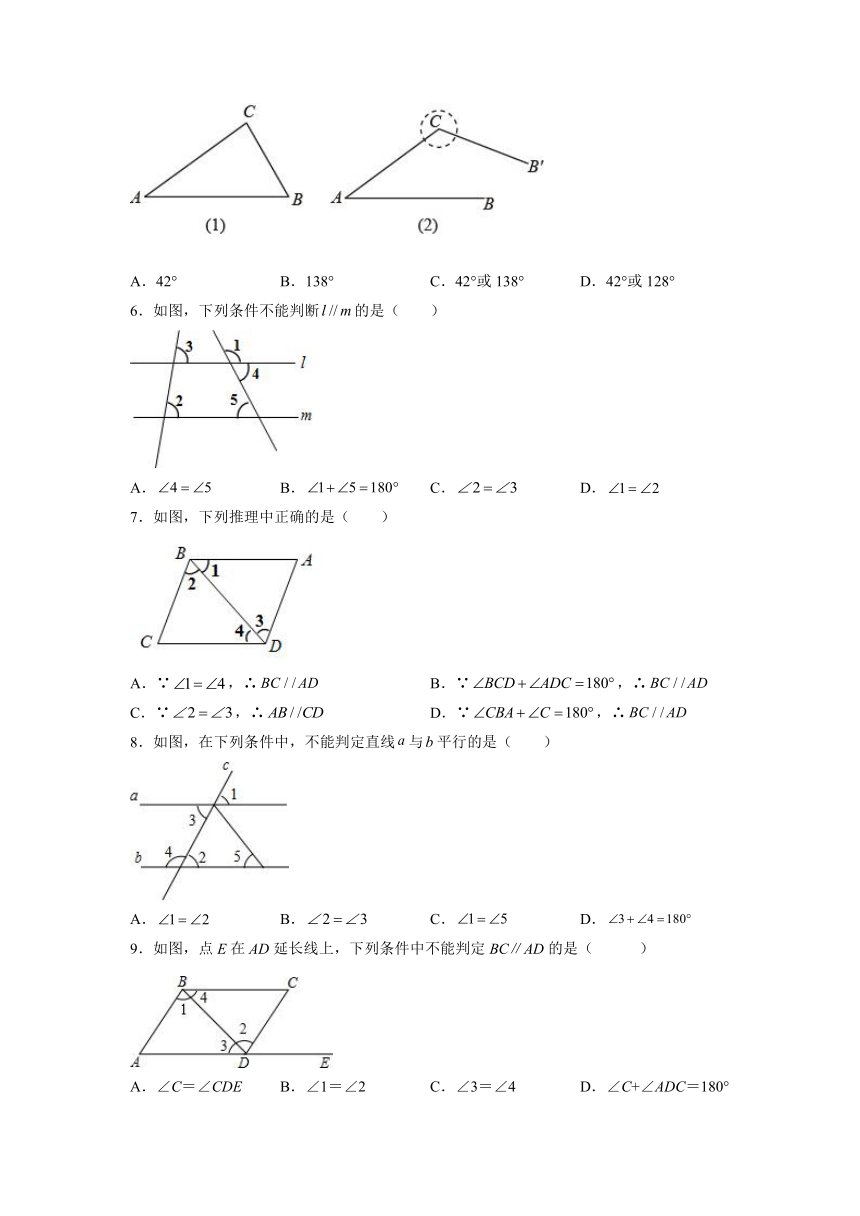
1.①a,b,c是直线,若a∥b,b∥c,则a∥c;②a,b,c是直线,若a⊥b,b⊥c,则a⊥c;③如果∠1=∠2,∠2=∠3,那么∠1=∠3;④互为邻补角的两个角相等.以上四个结论中正确的是( )
A.①② B.②③ C.③④ D.①③
2.如图,若∥,则下列结论中正确的是( )
A. B.
C. D.
3.如图,点A,B,E在同一条直线上,不能判定ADBC的条件是( )
A.∠A=∠CBE B.∠C+∠D=180°
C.∠C=∠CBE D.∠A+∠ABC=180°
4.如图,由两个完全相同的三角板拼成一个四边形,则下列条件能直接判断的是( )
A. B.
C. D.
5.如图(1),在中,,边绕点按逆时针方向旋转一周回到原来的位置.在旋转的过程中(图(2)),当( )时,.
A.42° B.138° C.42°或138° D.42°或128°
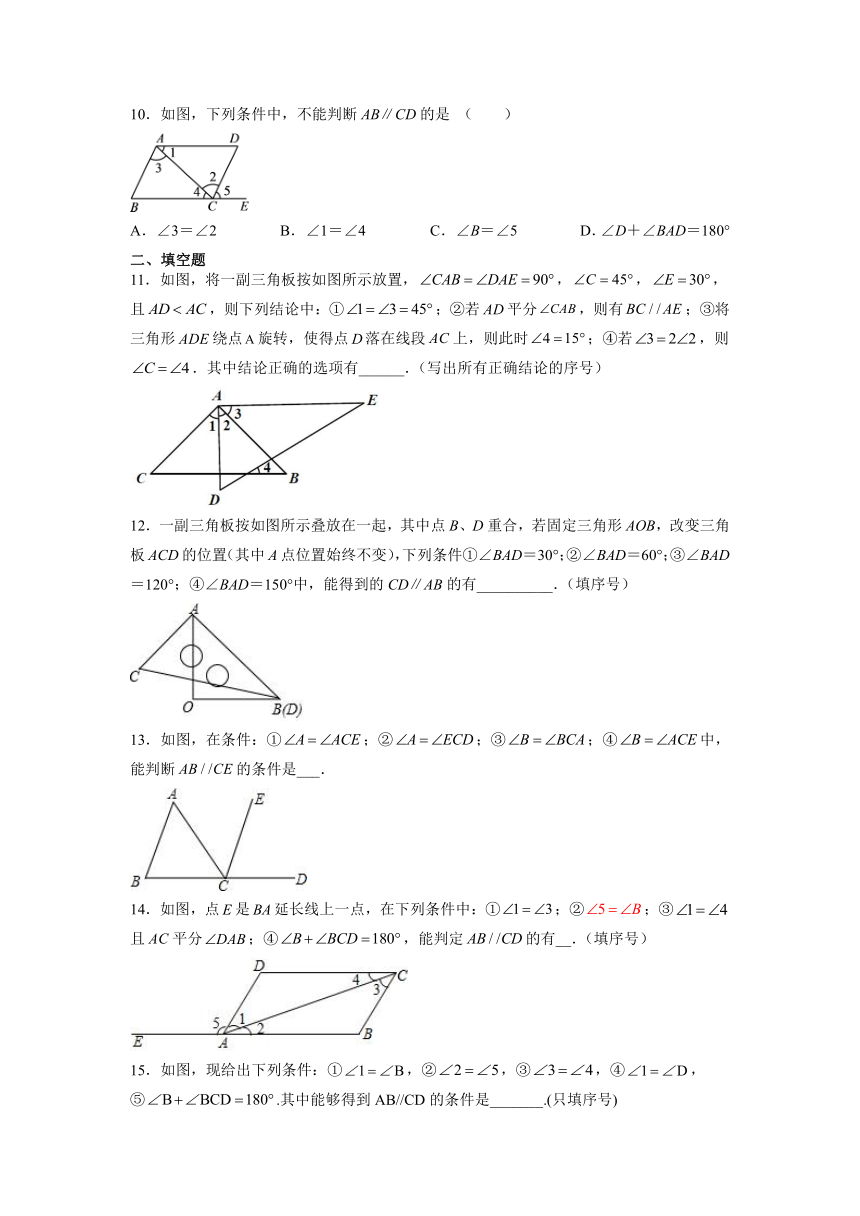
6.如图,下列条件不能判断的是( )
A. B. C. D.
7.如图,下列推理中正确的是( )
A.∵,∴ B.∵,∴
C.∵,∴ D.∵,∴
8.如图,在下列条件中,不能判定直线与平行的是( )
A. B. C. D.
9.如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( )
A.∠C=∠CDE B.∠1=∠2 C.∠3=∠4 D.∠C+∠ADC=180°
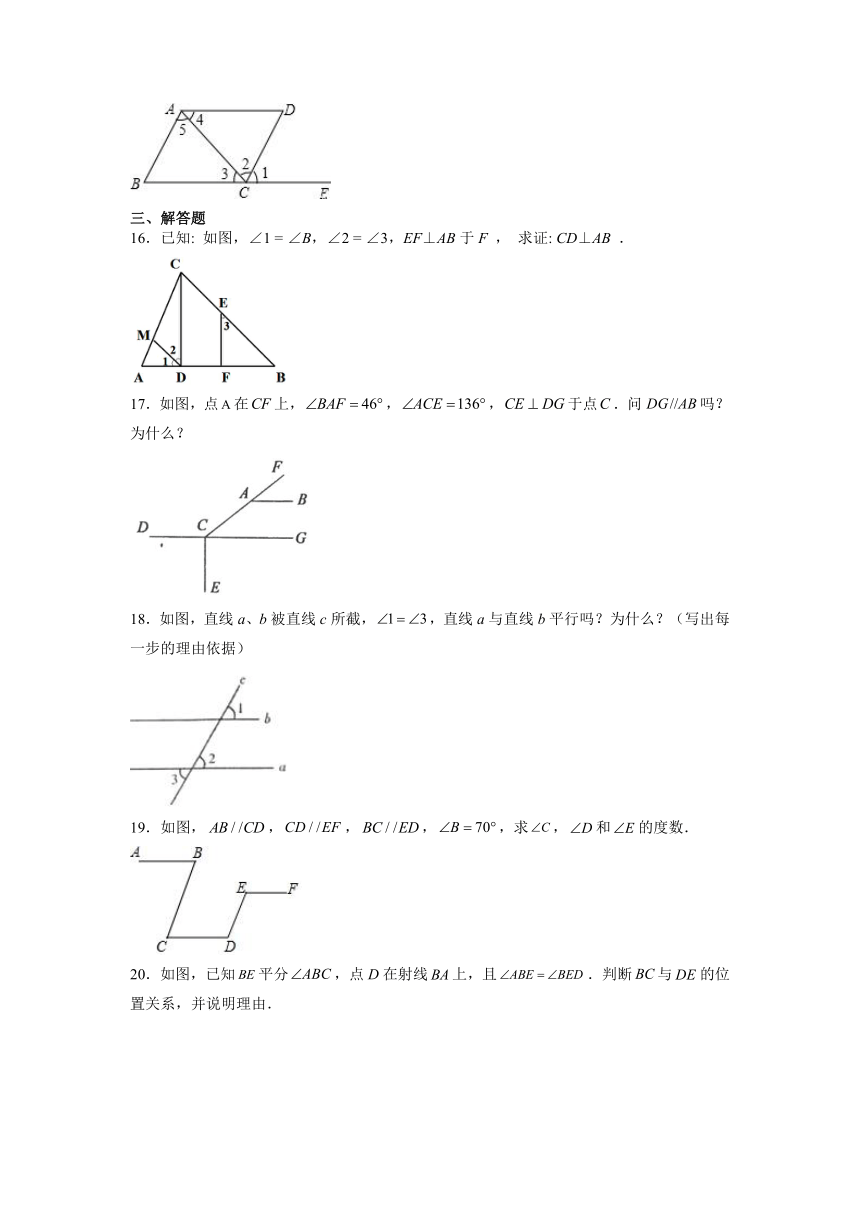
10.如图,下列条件中,不能判断AB∥CD的是 ( )
A.∠3=∠2 B.∠1=∠4 C.∠B=∠5 D.∠D+∠BAD=180°
二、填空题
11.如图,将一副三角板按如图所示放置,,,,且,则下列结论中:①;②若平分,则有;③将三角形绕点旋转,使得点落在线段上,则此时;④若,则.其中结论正确的选项有______.(写出所有正确结论的序号)
12.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),下列条件①∠BAD=30°;②∠BAD=60°;③∠BAD=120°;④∠BAD=150°中,能得到的CD∥AB的有__________.(填序号)
13.如图,在条件:①;②;③;④中,能判断的条件是___.
14.如图,点是延长线上一点,在下列条件中:①;②;③且平分;④,能判定的有__.(填序号)
15.如图,现给出下列条件:①,②,③,④,⑤.其中能够得到AB//CD的条件是_______.(只填序号)
三、解答题
16.已知: 如图,∠1 = ∠B,∠2 = ∠3,EF⊥AB于F , 求证: CD⊥AB .
17.如图,点在上,,,于点.问吗?为什么?
18.如图,直线a、b被直线c所截,,直线a与直线b平行吗?为什么?(写出每一步的理由依据)
19.如图,,,,,求,和的度数.
20.如图,已知平分,点D在射线上,且.判断与的位置关系,并说明理由.
21.如图,∠1=70°,∠2 =70°. 说明:AB∥CD.
22.如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
23.综合与探究
问题情境:如图,已知平分,于点D,E为延长线上一点,于点F,平分交于点G,.
问题发现:(1)如图1,当时,____________°;
(2)如图2,当为锐角时,与有什么数量关系,请说明理由;
拓展探究
(3)在(2)的条件下,已知直角三角形中两个锐角的和是90°,试探究和的位置关系,并证明结论;
(4)如图3,当为锐角时,若点E为线段上一点,于点F,平分交于点H,.请写出一个你发现的正确结论.
【参考答案】
1.D 2.C 3.C 4.A 5.C 6.D 7.B 8.C 9.B 10.B
11.②③④
12.①④
13.①
14.③④
15.①②⑤
16证明:∵∠1=∠B,
∴MD∥BC(同位角相等,两直线平行).
∴ ∠2=∠BCD(两直线平行,内错角相等)
又∵∠2 =∠3(已知)
∴∠3=∠BCD
∴EF∥CD(同位角相等,两直线平行)
又∵EF⊥AB(已知)
∴CD⊥AB.
17.解:,理由如下.
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
18.解:.
理由:与是对顶角,(两个角有公共顶点,并且一个角的两边分别是另一个角的两边的方向延长线)
.(对顶角相等)
,(已知)
,(等量代换)
.(同位角相等,两直线平行)
19.,,
,
,,
又,
,
∴∠D=110°,
.
20.解:BC∥DE;理由如下:
因为平分,
所以∠ABE=∠CBE,
因为,
所以∠CBE=∠BED,
所以BC∥DE.
21.如图:
∵∠1=70°,
∴∠3=∠1=70°,
又∵∠2 =70°,
∴∠3=∠2=70°,
∴ AB ∥CD.
22.证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
23.(1)∵,
∴,
∵,
∴,
∵平分,平分,
∴∠1=∠AOB=45,∠2=∠DEF=45,
∴;
故答案为:90;
(2).
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴;
(3)和的位置关系为OC∥GE.
证明:∵于点,
∴.
∴.
∵,
∴,
∴OC∥GE;
(4)答案不唯一,例如.
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴
一、选择题
1.①a,b,c是直线,若a∥b,b∥c,则a∥c;②a,b,c是直线,若a⊥b,b⊥c,则a⊥c;③如果∠1=∠2,∠2=∠3,那么∠1=∠3;④互为邻补角的两个角相等.以上四个结论中正确的是( )
A.①② B.②③ C.③④ D.①③
2.如图,若∥,则下列结论中正确的是( )
A. B.
C. D.
3.如图,点A,B,E在同一条直线上,不能判定ADBC的条件是( )
A.∠A=∠CBE B.∠C+∠D=180°
C.∠C=∠CBE D.∠A+∠ABC=180°
4.如图,由两个完全相同的三角板拼成一个四边形,则下列条件能直接判断的是( )
A. B.
C. D.
5.如图(1),在中,,边绕点按逆时针方向旋转一周回到原来的位置.在旋转的过程中(图(2)),当( )时,.
A.42° B.138° C.42°或138° D.42°或128°
6.如图,下列条件不能判断的是( )
A. B. C. D.
7.如图,下列推理中正确的是( )
A.∵,∴ B.∵,∴
C.∵,∴ D.∵,∴
8.如图,在下列条件中,不能判定直线与平行的是( )
A. B. C. D.
9.如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( )
A.∠C=∠CDE B.∠1=∠2 C.∠3=∠4 D.∠C+∠ADC=180°
10.如图,下列条件中,不能判断AB∥CD的是 ( )
A.∠3=∠2 B.∠1=∠4 C.∠B=∠5 D.∠D+∠BAD=180°
二、填空题
11.如图,将一副三角板按如图所示放置,,,,且,则下列结论中:①;②若平分,则有;③将三角形绕点旋转,使得点落在线段上,则此时;④若,则.其中结论正确的选项有______.(写出所有正确结论的序号)
12.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),下列条件①∠BAD=30°;②∠BAD=60°;③∠BAD=120°;④∠BAD=150°中,能得到的CD∥AB的有__________.(填序号)
13.如图,在条件:①;②;③;④中,能判断的条件是___.
14.如图,点是延长线上一点,在下列条件中:①;②;③且平分;④,能判定的有__.(填序号)
15.如图,现给出下列条件:①,②,③,④,⑤.其中能够得到AB//CD的条件是_______.(只填序号)
三、解答题
16.已知: 如图,∠1 = ∠B,∠2 = ∠3,EF⊥AB于F , 求证: CD⊥AB .
17.如图,点在上,,,于点.问吗?为什么?
18.如图,直线a、b被直线c所截,,直线a与直线b平行吗?为什么?(写出每一步的理由依据)
19.如图,,,,,求,和的度数.
20.如图,已知平分,点D在射线上,且.判断与的位置关系,并说明理由.
21.如图,∠1=70°,∠2 =70°. 说明:AB∥CD.
22.如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
23.综合与探究
问题情境:如图,已知平分,于点D,E为延长线上一点,于点F,平分交于点G,.
问题发现:(1)如图1,当时,____________°;
(2)如图2,当为锐角时,与有什么数量关系,请说明理由;
拓展探究
(3)在(2)的条件下,已知直角三角形中两个锐角的和是90°,试探究和的位置关系,并证明结论;
(4)如图3,当为锐角时,若点E为线段上一点,于点F,平分交于点H,.请写出一个你发现的正确结论.
【参考答案】
1.D 2.C 3.C 4.A 5.C 6.D 7.B 8.C 9.B 10.B
11.②③④
12.①④
13.①
14.③④
15.①②⑤
16证明:∵∠1=∠B,
∴MD∥BC(同位角相等,两直线平行).
∴ ∠2=∠BCD(两直线平行,内错角相等)
又∵∠2 =∠3(已知)
∴∠3=∠BCD
∴EF∥CD(同位角相等,两直线平行)
又∵EF⊥AB(已知)
∴CD⊥AB.
17.解:,理由如下.
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
18.解:.
理由:与是对顶角,(两个角有公共顶点,并且一个角的两边分别是另一个角的两边的方向延长线)
.(对顶角相等)
,(已知)
,(等量代换)
.(同位角相等,两直线平行)
19.,,
,
,,
又,
,
∴∠D=110°,
.
20.解:BC∥DE;理由如下:
因为平分,
所以∠ABE=∠CBE,
因为,
所以∠CBE=∠BED,
所以BC∥DE.
21.如图:
∵∠1=70°,
∴∠3=∠1=70°,
又∵∠2 =70°,
∴∠3=∠2=70°,
∴ AB ∥CD.
22.证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
23.(1)∵,
∴,
∵,
∴,
∵平分,平分,
∴∠1=∠AOB=45,∠2=∠DEF=45,
∴;
故答案为:90;
(2).
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴;
(3)和的位置关系为OC∥GE.
证明:∵于点,
∴.
∴.
∵,
∴,
∴OC∥GE;
(4)答案不唯一,例如.
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴
