2021-2022学年人教版七年级数学下册5.2平行线及其判定课后练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2平行线及其判定课后练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 16:04:02 | ||
图片预览


文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线
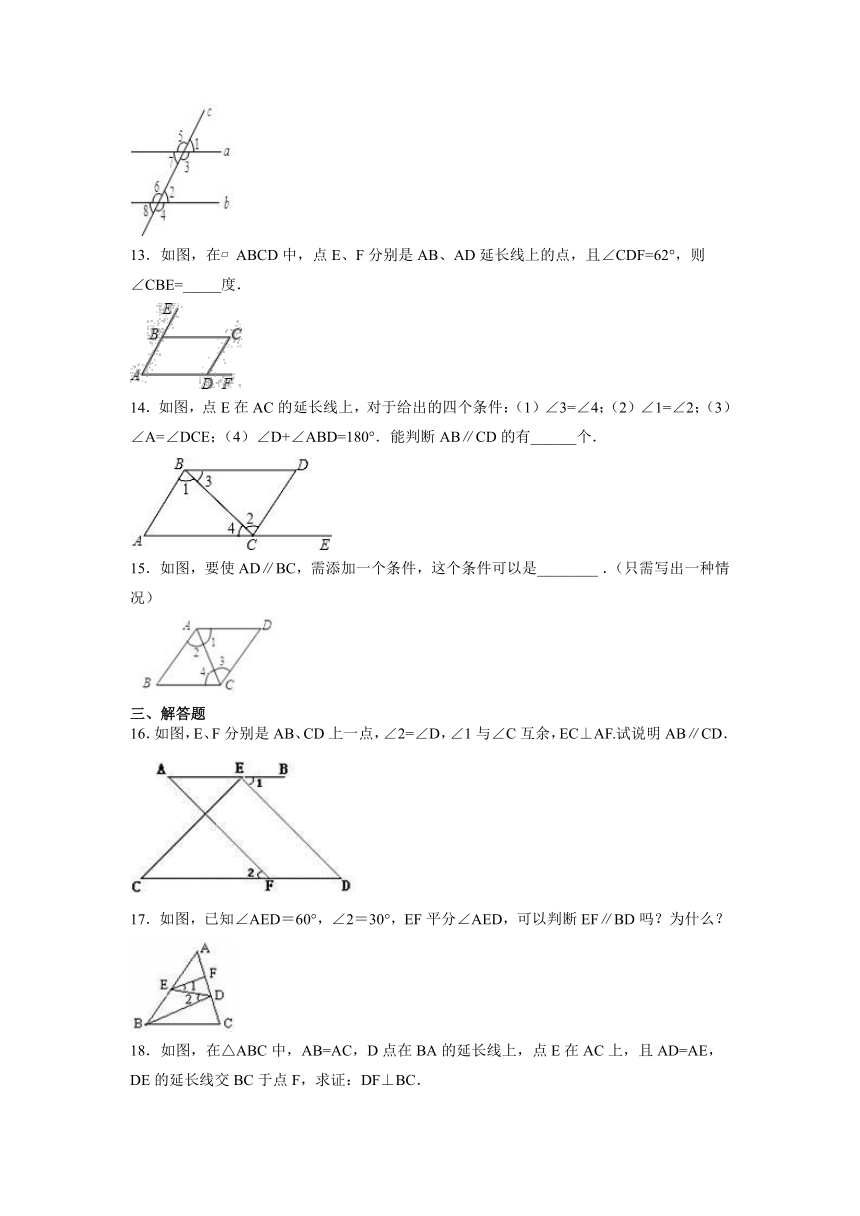
5.2平行线及其判定课后练习
一、选择题
1.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的两条直线平行.
A.①②③ B.①②④ C.①③④ D.①③
2.在同一平面内两条不重合的直线的位置关系是( )
A.平行或垂直 B.平行或相交 C.垂直或相交 D.以上都不对
3.在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行 B.相交 C.重合 D.以上都有可能
4.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于( )时,AB∥CD.
A.50° B.40° C.30° D.60°
5.如图,下列说法中,正确的是( )
A.因为∠A+∠D=180°,所以AD∥BC B.因为∠C+∠D=180°,所以AB∥CD
C.因为∠A+∠D=180°,所以AB∥CD D.因为∠A+∠C=180°,所以AB∥CD
6.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠3+∠4=180°;④∠1+∠2=180°;⑤∠1+∠2=90°; ⑥∠3+∠4=90°; ⑦∠1=∠4,能判断直线l1∥l2的条件有( )
A.②④ B.①②⑦ C.③④ D.②③⑥
7.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
A.70° B.50° C.30° D.20°
8.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,能判定AB∥CD的条件是( ).
A.∠ACB+∠B=180° B.∠ACD=∠B C.∠ACD=∠A D.∠DCE=∠A
10.已知长方体ABCD﹣EFGH如图所示,那么下列直线中与直线AB不平行也不垂直的直线是( )
A.EA B.GH C.HC D.EF
二、填空题
11.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______
12.如图,直线a和直线b被直线c所截,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是________.
13.如图,在 ABCD中,点E、F分别是AB、AD延长线上的点,且∠CDF=62°,则∠CBE=_____度.
14.如图,点E在AC的延长线上,对于给出的四个条件:(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有______个.
15.如图,要使AD∥BC,需添加一个条件,这个条件可以是________ .(只需写出一种情况)
三、解答题
16.如图,E、F分别是AB、CD上一点,∠2=∠D,∠1与∠C互余,EC⊥AF.试说明AB∥CD.
17.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
18.如图,在△ABC中,AB=AC,D点在BA的延长线上,点E在AC上,且AD=AE,DE的延长线交BC于点F,求证:DF⊥BC.
19.已知:如图,B、F、C、D在同一条直线上,∠ACB=∠EFD,BF=CD,AC=EF.求证:AB∥ED.
20.如图,在△ABC中,∠B=54°,AD平分∠CAB,交BC于D,E为AC边上一点,连结DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.
21.如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
22.如图,已知∠1=∠D,∠1+∠A=180°,可得哪些直线互相平行?请说明理由.
23.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=75°.求∠BCA的度数.
【参考答案】
1.C 2.B 3.B 4.A 5.C 6.C 7.D 8.B 9.C 10.C
11.平行
12.①②③④;
13.62
14.3
15.∠1=∠4或∠DAB+∠B=180°或∠D+∠DCB=180°
16.证明:∵EC⊥AF,
∴∠2+∠C=90°,
又∵∠1与∠C互余,
∴∠1+∠C=90°,
∴∠1=∠2,
∵∠2=∠D,
∴∠1=∠D,
∴AB∥CD.
17 . EF∥BD;理由如下:
∵∠AED=60°,EF平分∠AED,
∴∠FED=30°,
又∵∠FED=∠2=30°,
∴EF∥BD
18.证明:如图,过A作AM⊥BC于M,
∵AB=AC,∴∠BAC=2∠BAM,∵AD=AE,∴∠D=∠AED,∴∠BAC=∠D+∠AED=2∠D,∴∠BAC=2∠BAM=2∠D,∴∠BAM=∠D,∴DF∥AM,∵AM⊥BC,∴DF⊥BC.
19.先根据BF=CD得出BC=DF,∵BF=CD,∴BF+FC=CD+FC,即BC=DF.又∵在△ABC与△EDF中,∠ACB=∠EFD,AC=EF(已知),∴△ABC≌△EDF(SAS),∴∠B=∠D(全等三角形的对应角相等),∴AB∥ED(内错角相等,两直线平行).
考点:1.全等三角形的判定;2.平行线的判定..
20.∵∠BAD=∠DAC,∠ EAD=∠EDA,∴∠BAD=∠EDA,∴DE//AB,∴∠EDF=∠B=54°,∵∠EFD=90°,∴∠FED =90°-∠EDF=36°;
考点:1.平行线的判定与性质;2.直角三角形的性质.
21.解:AB与DG平行.
∵AD⊥BC,EF⊥BC(已知),∴∠EFB=9°,∠ADB=90°(垂直定义),∴∠EFB=∠ADB(等量代换),
∴EF∥AD(同位角相等,两直线平行),
∴∠1=∠BAD(两直线平行,同位角相等).
∵∠1=∠2(已知),∴∠2=∠BAD(等量代换),
∴AB∥DG(内错角相等,两直线平行).
22.可知AD∥BC,AB∥DC.
理由:因为∠1=∠D,
所以AD∥BC(内错角相等,两直线平行).
因为∠1+∠A=180°,∠1=∠D,
所以∠D+∠A=180°,
所以AB∥DC(同旁内角互补,两直线平行).
23.因为CD⊥AB,FE⊥AB,所以CD∥EF,所以∠2=∠BCD,因为∠1=∠2,所以∠1=∠BCD,所以DG∥BC,所以∠BCA=∠3=75°.
5.2平行线及其判定课后练习
一、选择题
1.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的两条直线平行.
A.①②③ B.①②④ C.①③④ D.①③
2.在同一平面内两条不重合的直线的位置关系是( )
A.平行或垂直 B.平行或相交 C.垂直或相交 D.以上都不对
3.在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行 B.相交 C.重合 D.以上都有可能
4.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于( )时,AB∥CD.
A.50° B.40° C.30° D.60°
5.如图,下列说法中,正确的是( )
A.因为∠A+∠D=180°,所以AD∥BC B.因为∠C+∠D=180°,所以AB∥CD
C.因为∠A+∠D=180°,所以AB∥CD D.因为∠A+∠C=180°,所以AB∥CD
6.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠3+∠4=180°;④∠1+∠2=180°;⑤∠1+∠2=90°; ⑥∠3+∠4=90°; ⑦∠1=∠4,能判断直线l1∥l2的条件有( )
A.②④ B.①②⑦ C.③④ D.②③⑥
7.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
A.70° B.50° C.30° D.20°
8.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,能判定AB∥CD的条件是( ).
A.∠ACB+∠B=180° B.∠ACD=∠B C.∠ACD=∠A D.∠DCE=∠A
10.已知长方体ABCD﹣EFGH如图所示,那么下列直线中与直线AB不平行也不垂直的直线是( )
A.EA B.GH C.HC D.EF
二、填空题
11.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______
12.如图,直线a和直线b被直线c所截,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是________.
13.如图,在 ABCD中,点E、F分别是AB、AD延长线上的点,且∠CDF=62°,则∠CBE=_____度.
14.如图,点E在AC的延长线上,对于给出的四个条件:(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有______个.
15.如图,要使AD∥BC,需添加一个条件,这个条件可以是________ .(只需写出一种情况)
三、解答题
16.如图,E、F分别是AB、CD上一点,∠2=∠D,∠1与∠C互余,EC⊥AF.试说明AB∥CD.
17.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
18.如图,在△ABC中,AB=AC,D点在BA的延长线上,点E在AC上,且AD=AE,DE的延长线交BC于点F,求证:DF⊥BC.
19.已知:如图,B、F、C、D在同一条直线上,∠ACB=∠EFD,BF=CD,AC=EF.求证:AB∥ED.
20.如图,在△ABC中,∠B=54°,AD平分∠CAB,交BC于D,E为AC边上一点,连结DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.
21.如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
22.如图,已知∠1=∠D,∠1+∠A=180°,可得哪些直线互相平行?请说明理由.
23.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=75°.求∠BCA的度数.
【参考答案】
1.C 2.B 3.B 4.A 5.C 6.C 7.D 8.B 9.C 10.C
11.平行
12.①②③④;
13.62
14.3
15.∠1=∠4或∠DAB+∠B=180°或∠D+∠DCB=180°
16.证明:∵EC⊥AF,
∴∠2+∠C=90°,
又∵∠1与∠C互余,
∴∠1+∠C=90°,
∴∠1=∠2,
∵∠2=∠D,
∴∠1=∠D,
∴AB∥CD.
17 . EF∥BD;理由如下:
∵∠AED=60°,EF平分∠AED,
∴∠FED=30°,
又∵∠FED=∠2=30°,
∴EF∥BD
18.证明:如图,过A作AM⊥BC于M,
∵AB=AC,∴∠BAC=2∠BAM,∵AD=AE,∴∠D=∠AED,∴∠BAC=∠D+∠AED=2∠D,∴∠BAC=2∠BAM=2∠D,∴∠BAM=∠D,∴DF∥AM,∵AM⊥BC,∴DF⊥BC.
19.先根据BF=CD得出BC=DF,∵BF=CD,∴BF+FC=CD+FC,即BC=DF.又∵在△ABC与△EDF中,∠ACB=∠EFD,AC=EF(已知),∴△ABC≌△EDF(SAS),∴∠B=∠D(全等三角形的对应角相等),∴AB∥ED(内错角相等,两直线平行).
考点:1.全等三角形的判定;2.平行线的判定..
20.∵∠BAD=∠DAC,∠ EAD=∠EDA,∴∠BAD=∠EDA,∴DE//AB,∴∠EDF=∠B=54°,∵∠EFD=90°,∴∠FED =90°-∠EDF=36°;
考点:1.平行线的判定与性质;2.直角三角形的性质.
21.解:AB与DG平行.
∵AD⊥BC,EF⊥BC(已知),∴∠EFB=9°,∠ADB=90°(垂直定义),∴∠EFB=∠ADB(等量代换),
∴EF∥AD(同位角相等,两直线平行),
∴∠1=∠BAD(两直线平行,同位角相等).
∵∠1=∠2(已知),∴∠2=∠BAD(等量代换),
∴AB∥DG(内错角相等,两直线平行).
22.可知AD∥BC,AB∥DC.
理由:因为∠1=∠D,
所以AD∥BC(内错角相等,两直线平行).
因为∠1+∠A=180°,∠1=∠D,
所以∠D+∠A=180°,
所以AB∥DC(同旁内角互补,两直线平行).
23.因为CD⊥AB,FE⊥AB,所以CD∥EF,所以∠2=∠BCD,因为∠1=∠2,所以∠1=∠BCD,所以DG∥BC,所以∠BCA=∠3=75°.
