2021-2022年初中数学九年级下册27.2.2相似三角形的性质课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022年初中数学九年级下册27.2.2相似三角形的性质课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 492.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 00:00:00 | ||
图片预览


文档简介
2021-2022年初中数学九年级下册同步(人教版)
27.2.2相似三角形的性质-课堂练习
一、单选题
1.如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
2.两个三角形的相似比是3:2,则其面积之比是( )
A.3:2 B.2:3 C.9:4 D.27:8
3.两个相似多边形的面积之比为1:3,则它们的周长之比为 ( )
A.1:3 B.1:9 C. D.2:3
4.如图,在△ABC中,以AB为直径作, 交AC于点E ,BC于点D ,CD=BD ,则( )
A.AC=BC B. C.AB=DE D.BC BD=AB CE
5.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
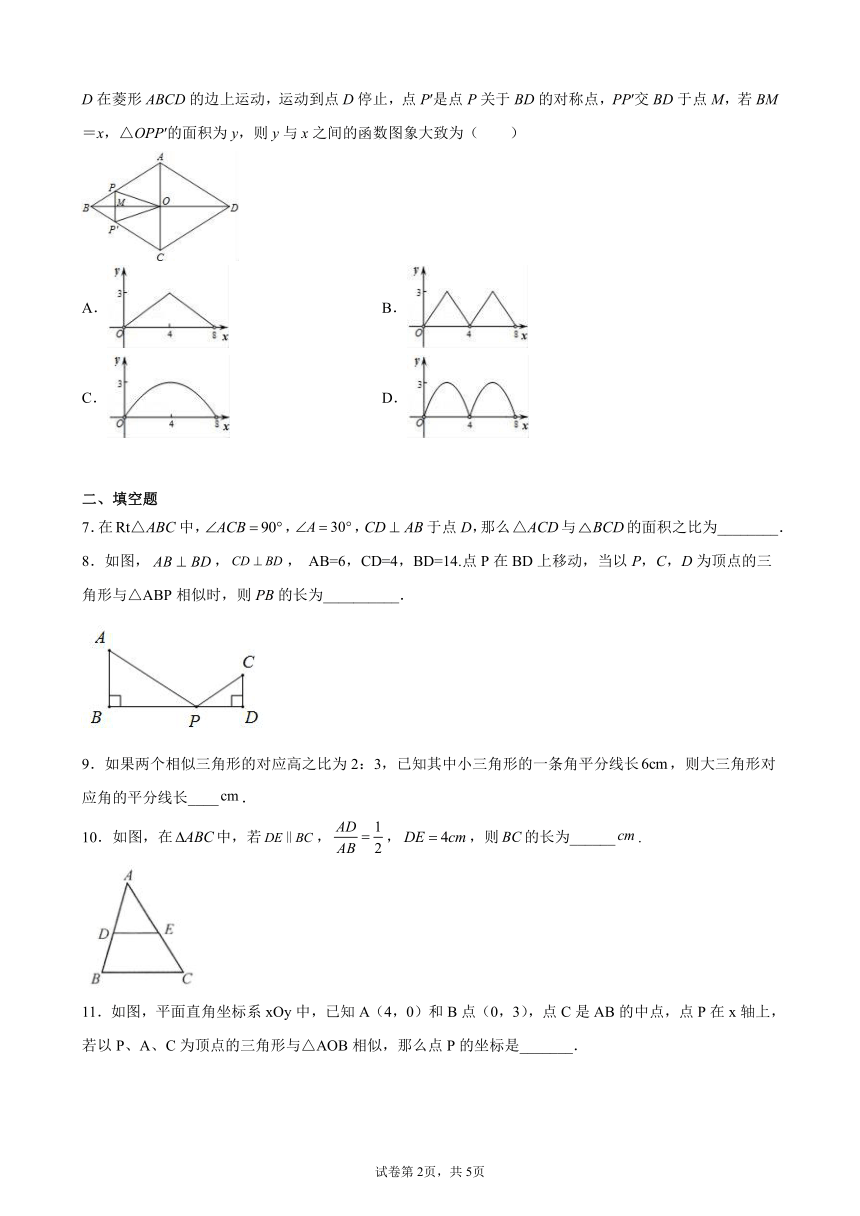
6.如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A. B.
C. D.
二、填空题
7.在中,,,于点D,那么与的面积之比为________.
8.如图,,, AB=6,CD=4,BD=14.点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,则PB的长为__________.
9.如果两个相似三角形的对应高之比为2:3,已知其中小三角形的一条角平分线长,则大三角形对应角的平分线长____.
10.如图,在中,若,,,则的长为______.
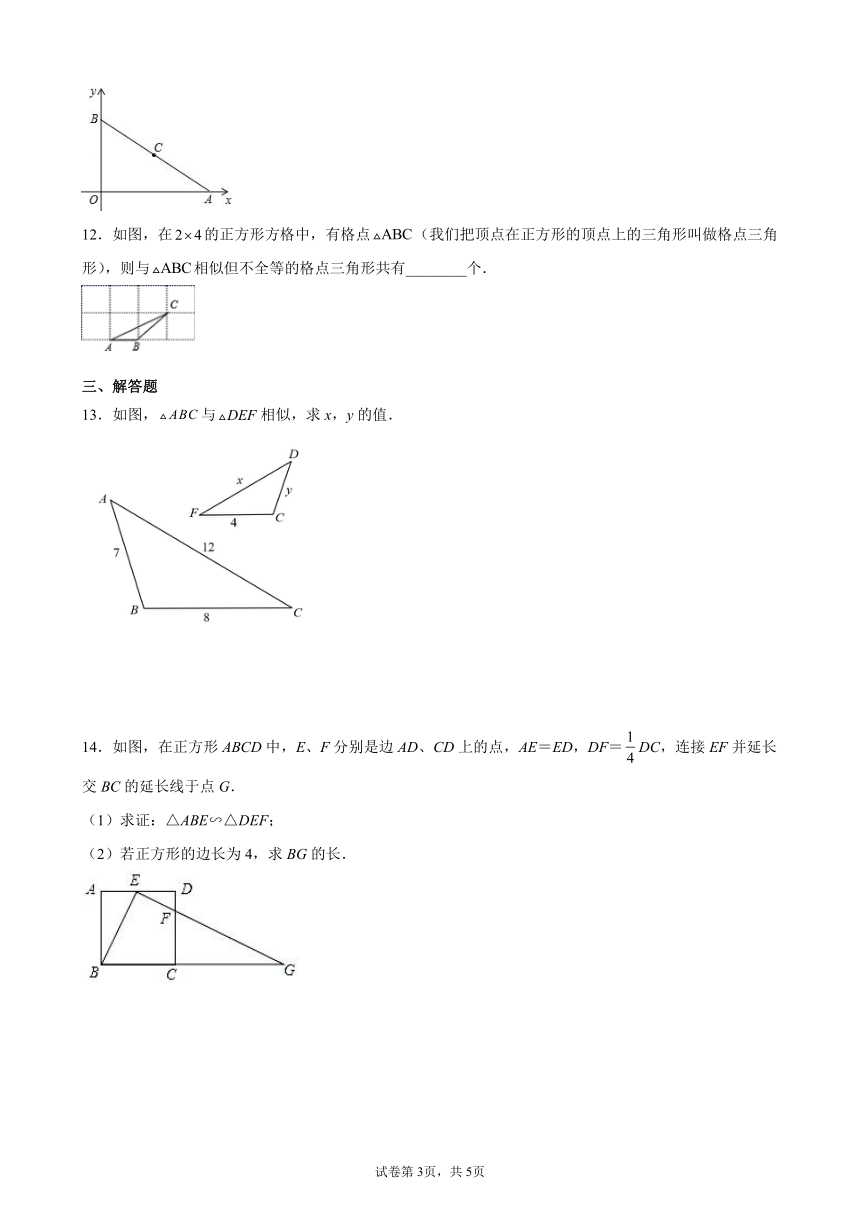
11.如图,平面直角坐标系xOy中,已知A(4,0)和B点(0,3),点C是AB的中点,点P在x轴上,若以P、A、C为顶点的三角形与△AOB相似,那么点P的坐标是_______.
12.如图,在的正方形方格中,有格点(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与相似但不全等的格点三角形共有________个.
三、解答题
13.如图,与相似,求x,y的值.
14.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
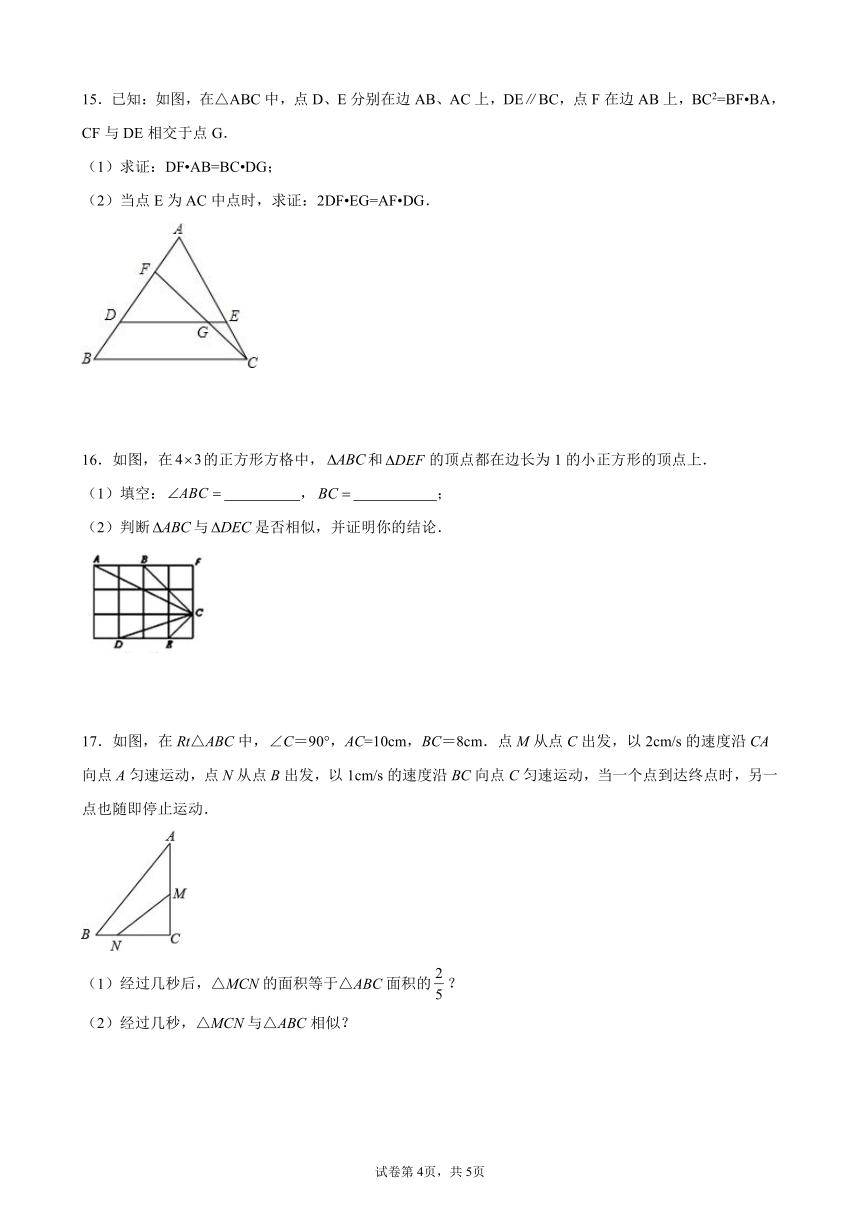
15.已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,点F在边AB上,BC2=BF BA,CF与DE相交于点G.
(1)求证:DF AB=BC DG;
(2)当点E为AC中点时,求证:2DF EG=AF DG.
16.如图,在的正方形方格中,和的顶点都在边长为1的小正方形的顶点上.
(1)填空: , ;
(2)判断与是否相似,并证明你的结论.
17.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
18.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.
试卷第4页,共5页
试卷第5页,共5页
参考答案
1.A
【解析】解:由题意:①②④中,∠ABC=∠ADE=∠AFH=135°,
又∵,
∴,,
∴△ABC∽△ADE∽△HFA,
故选:A.
2.C
【解析】解:因为两个三角形的相似比是3:2,则其面积之比是9:4;
故选C.
3.C
【解析】相似比是1:,所以周长比是1:,选C.
4.D
【解析】解:如图,连接AD、DE,
∵直径AB是⊙O的直径,
∴∠ADB=90°,
∵ CD=BD,
∴AC=AB,
故选项A错误;
∴∠CAD=∠BAD,
∴DE=BD, ,
∴,
∴,且得不到,
故选项B、C错误;
∵四边形ABDE是⊙O的内接四边形,
∴∠CDE=∠CAB,
∵∠C=∠C,
∴△CDE∽△CAB,
∴ ,
∴BC·DE=AB·CE,
∵DE=BD,
∴BC·BD=AB·CE.
故选:D
5.B
【解析】∵在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,设CF=x,则CD=4x,∴DF=3x,BE=EC=2x,∴ AB:EC=BE:CF=2:1.∵∠B=∠C=90°,∴△ABE∽△ECF,∴AB:EC=AE:EF,∠AEB=∠EFC.∵BE=CE,∴AB:AE=BE:EF,
∵∠FEC+∠EFC=90°,∠AEB=∠EFC,∴∠AEB+∠FEC=90°,∴∠AEF=∠B=90°,∴△ABE∽△AEF,AE⊥EF,∴②③正确.
故选B.
6.D
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=AC=3,OB=BD=4,AC⊥BD,
①当BM≤4时,
∵点P′与点P关于BD对称,
∴P′P⊥BD,
∴P′P∥AC,
∴△P′BP∽△CBA,
∴,即,
∴PP′=,
∵OM=4-x,
∴△OPP′的面积y=PP′ OM=×;
∴y与x之间的函数图象是抛物线,开口向下,过(0,0)和(4,0);
②当BM≥4时,y与x之间的函数图象的形状与①中的相同,过(4,0)和(8,0);
综上所述:y与x之间的函数图象大致为
.
故选D.
7.
【解析】解:如图,
故答案为:
8.8.4或2或12
【解析】若,
∴,
设 ,
,
,
解得;
若,
∴,
设,
,
,
解得 ,
综上所述,BP的长度为8.4或2或12,
故答案为:8.4或2或12.
9.9
【解析】解:设大三角形对应角的角平分线长是xcm,
由题意得,, 解得x=9.
故答案为:9.
10.8
【解析】解:∵DE∥BC,
∴△ADE∽△ABC,
∴
即
∴BC=8(cm)
故答案是:8
11.(2,0)或(,0)
【解析】解:∵A(4,0)和B点(0,3),
∴OA=4,OB=3,
∴AB=5,
∵C是AB的中点,
∴AC=2.5,
设P(x,0),
由题意可知点P在点A的左侧,
∴AP=4﹣x,
∵以P、A、C为顶点的三角形与△AOB相似,
∴有△APC∽△AOB和△ACP∽△AOB两种情况,
当△APC∽△AOB时,则,即,解得x=2,
∴P(2,0);
当△ACP∽△AOB时,则,即,解得x=,
∴P(,0);
综上可知P点坐标为(2,0)或(,0).
故答案为:(2,0)或(,0).
12.20.
【解析】解:∵△ABC的三边长:AB=1,BC=,AC=,
又∵在的正方形方格中,最大的线段长为,
∴可将三角形扩大倍,这样的三角形有16个;扩大2倍,这样的三角形有4个;
所以符合题意的三角形共有20个.
故答案为20.
13.,或x= ,y=.
【解析】解:∵△ABC与△DEF相似,∠B、∠E为钝角,
∴∠B=∠E,
∴当,即时,△ABC∽△DEF,
解得:x=6,y= ;
当,即时,△ABC∽△FED,
解得:x= ,y=,
∴x=6,y=或x= ,y=.
14.(1)见解析;(2)
【解析】(1)证明:∵四边形ABCD为正方形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴;
(2)解:∵四边形ABCD为正方形,
∴,
∴,
∵,
,
∴,
又∵,正方形的边长为4,
∴,,
∴.
15.(1)证明见解析;(2)证明见解析.
【解析】证明:(1)∵BC2=BF BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴,
∵DE∥BC,
∴,
∴,
∴DF:BC=DG:BA,
∴DF AB=BC DG;
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
为的中位线,
∴AH=2EG,
∵AH∥DG,
∴,
∴,
∴,
即2DF EG=AF DG.
16.(1),;(2)相似,理由见解析
【解析】解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴;
故答案为:,;
(2)解:相似.理由如下:
∵,,
∴,
∴
又∵
∴.
17.(1)4秒;(2)或秒
【解析】解:(1)设经过x秒,△MCN的面积等于△ABC面积的,
则有MC=2x,NC=8-x,
∴×2x(8-x)=×8×10×,
解得x1=x2=4,
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似,
∵∠C=∠C,
∴可分为两种情况:
①,
即,
解得t=;
②,即,
解得t=.
答:经过或秒,△MCN与△ABC相似.
18.(1)证明见解析;(2);(3)线段AD、AB、CD之间数量关系:AD=AB+CD;理由见解析.
【解析】(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴ ,
∴,
∴CD=;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFE,
∴AF=AB,
∴AD=AF+DF=AB+CD.
答案第10页,共1页
答案第9页,共9页
27.2.2相似三角形的性质-课堂练习
一、单选题
1.如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
2.两个三角形的相似比是3:2,则其面积之比是( )
A.3:2 B.2:3 C.9:4 D.27:8
3.两个相似多边形的面积之比为1:3,则它们的周长之比为 ( )
A.1:3 B.1:9 C. D.2:3
4.如图,在△ABC中,以AB为直径作, 交AC于点E ,BC于点D ,CD=BD ,则( )
A.AC=BC B. C.AB=DE D.BC BD=AB CE
5.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A. B.
C. D.
二、填空题
7.在中,,,于点D,那么与的面积之比为________.
8.如图,,, AB=6,CD=4,BD=14.点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,则PB的长为__________.
9.如果两个相似三角形的对应高之比为2:3,已知其中小三角形的一条角平分线长,则大三角形对应角的平分线长____.
10.如图,在中,若,,,则的长为______.
11.如图,平面直角坐标系xOy中,已知A(4,0)和B点(0,3),点C是AB的中点,点P在x轴上,若以P、A、C为顶点的三角形与△AOB相似,那么点P的坐标是_______.
12.如图,在的正方形方格中,有格点(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与相似但不全等的格点三角形共有________个.
三、解答题
13.如图,与相似,求x,y的值.
14.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
15.已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,点F在边AB上,BC2=BF BA,CF与DE相交于点G.
(1)求证:DF AB=BC DG;
(2)当点E为AC中点时,求证:2DF EG=AF DG.
16.如图,在的正方形方格中,和的顶点都在边长为1的小正方形的顶点上.
(1)填空: , ;
(2)判断与是否相似,并证明你的结论.
17.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
18.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.
试卷第4页,共5页
试卷第5页,共5页
参考答案
1.A
【解析】解:由题意:①②④中,∠ABC=∠ADE=∠AFH=135°,
又∵,
∴,,
∴△ABC∽△ADE∽△HFA,
故选:A.
2.C
【解析】解:因为两个三角形的相似比是3:2,则其面积之比是9:4;
故选C.
3.C
【解析】相似比是1:,所以周长比是1:,选C.
4.D
【解析】解:如图,连接AD、DE,
∵直径AB是⊙O的直径,
∴∠ADB=90°,
∵ CD=BD,
∴AC=AB,
故选项A错误;
∴∠CAD=∠BAD,
∴DE=BD, ,
∴,
∴,且得不到,
故选项B、C错误;
∵四边形ABDE是⊙O的内接四边形,
∴∠CDE=∠CAB,
∵∠C=∠C,
∴△CDE∽△CAB,
∴ ,
∴BC·DE=AB·CE,
∵DE=BD,
∴BC·BD=AB·CE.
故选:D
5.B
【解析】∵在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,设CF=x,则CD=4x,∴DF=3x,BE=EC=2x,∴ AB:EC=BE:CF=2:1.∵∠B=∠C=90°,∴△ABE∽△ECF,∴AB:EC=AE:EF,∠AEB=∠EFC.∵BE=CE,∴AB:AE=BE:EF,
∵∠FEC+∠EFC=90°,∠AEB=∠EFC,∴∠AEB+∠FEC=90°,∴∠AEF=∠B=90°,∴△ABE∽△AEF,AE⊥EF,∴②③正确.
故选B.
6.D
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=AC=3,OB=BD=4,AC⊥BD,
①当BM≤4时,
∵点P′与点P关于BD对称,
∴P′P⊥BD,
∴P′P∥AC,
∴△P′BP∽△CBA,
∴,即,
∴PP′=,
∵OM=4-x,
∴△OPP′的面积y=PP′ OM=×;
∴y与x之间的函数图象是抛物线,开口向下,过(0,0)和(4,0);
②当BM≥4时,y与x之间的函数图象的形状与①中的相同,过(4,0)和(8,0);
综上所述:y与x之间的函数图象大致为
.
故选D.
7.
【解析】解:如图,
故答案为:
8.8.4或2或12
【解析】若,
∴,
设 ,
,
,
解得;
若,
∴,
设,
,
,
解得 ,
综上所述,BP的长度为8.4或2或12,
故答案为:8.4或2或12.
9.9
【解析】解:设大三角形对应角的角平分线长是xcm,
由题意得,, 解得x=9.
故答案为:9.
10.8
【解析】解:∵DE∥BC,
∴△ADE∽△ABC,
∴
即
∴BC=8(cm)
故答案是:8
11.(2,0)或(,0)
【解析】解:∵A(4,0)和B点(0,3),
∴OA=4,OB=3,
∴AB=5,
∵C是AB的中点,
∴AC=2.5,
设P(x,0),
由题意可知点P在点A的左侧,
∴AP=4﹣x,
∵以P、A、C为顶点的三角形与△AOB相似,
∴有△APC∽△AOB和△ACP∽△AOB两种情况,
当△APC∽△AOB时,则,即,解得x=2,
∴P(2,0);
当△ACP∽△AOB时,则,即,解得x=,
∴P(,0);
综上可知P点坐标为(2,0)或(,0).
故答案为:(2,0)或(,0).
12.20.
【解析】解:∵△ABC的三边长:AB=1,BC=,AC=,
又∵在的正方形方格中,最大的线段长为,
∴可将三角形扩大倍,这样的三角形有16个;扩大2倍,这样的三角形有4个;
所以符合题意的三角形共有20个.
故答案为20.
13.,或x= ,y=.
【解析】解:∵△ABC与△DEF相似,∠B、∠E为钝角,
∴∠B=∠E,
∴当,即时,△ABC∽△DEF,
解得:x=6,y= ;
当,即时,△ABC∽△FED,
解得:x= ,y=,
∴x=6,y=或x= ,y=.
14.(1)见解析;(2)
【解析】(1)证明:∵四边形ABCD为正方形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴;
(2)解:∵四边形ABCD为正方形,
∴,
∴,
∵,
,
∴,
又∵,正方形的边长为4,
∴,,
∴.
15.(1)证明见解析;(2)证明见解析.
【解析】证明:(1)∵BC2=BF BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴,
∵DE∥BC,
∴,
∴,
∴DF:BC=DG:BA,
∴DF AB=BC DG;
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
为的中位线,
∴AH=2EG,
∵AH∥DG,
∴,
∴,
∴,
即2DF EG=AF DG.
16.(1),;(2)相似,理由见解析
【解析】解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴;
故答案为:,;
(2)解:相似.理由如下:
∵,,
∴,
∴
又∵
∴.
17.(1)4秒;(2)或秒
【解析】解:(1)设经过x秒,△MCN的面积等于△ABC面积的,
则有MC=2x,NC=8-x,
∴×2x(8-x)=×8×10×,
解得x1=x2=4,
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似,
∵∠C=∠C,
∴可分为两种情况:
①,
即,
解得t=;
②,即,
解得t=.
答:经过或秒,△MCN与△ABC相似.
18.(1)证明见解析;(2);(3)线段AD、AB、CD之间数量关系:AD=AB+CD;理由见解析.
【解析】(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴ ,
∴,
∴CD=;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFE,
∴AF=AB,
∴AD=AF+DF=AB+CD.
答案第10页,共1页
答案第9页,共9页
