北师大版2021-2022年初中数学七年级下册4.2图形的全等课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学七年级下册4.2图形的全等课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 454.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 20:06:50 | ||
图片预览


文档简介
2021-2022年初中数学七年级下册同步(北师大版)
4.2图形的全等-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列各组图形中,是全等图形的是( )
A. B. C. D.
2.一个正方体的展开图有( )个全等的正方形.
A.2个 B.3个 C.4个 D.6个
3.如图,下面4个正方形的边长都相等,其中阴影部分的面积相等的图形有( )
A.0个 B.2个 C.3个 D.4个
4.用两个全等的直角三角形拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)正方形;(4)等腰三角形,一定可以拼成的图形是 ( )
A.(1)(2)(4) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(3)
5.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等
C.完全重合的两个三角形全等 D.所有的等腰三角形都全等
6.如图,,,则的对应边是( )
A. B. C. D.
二、填空题
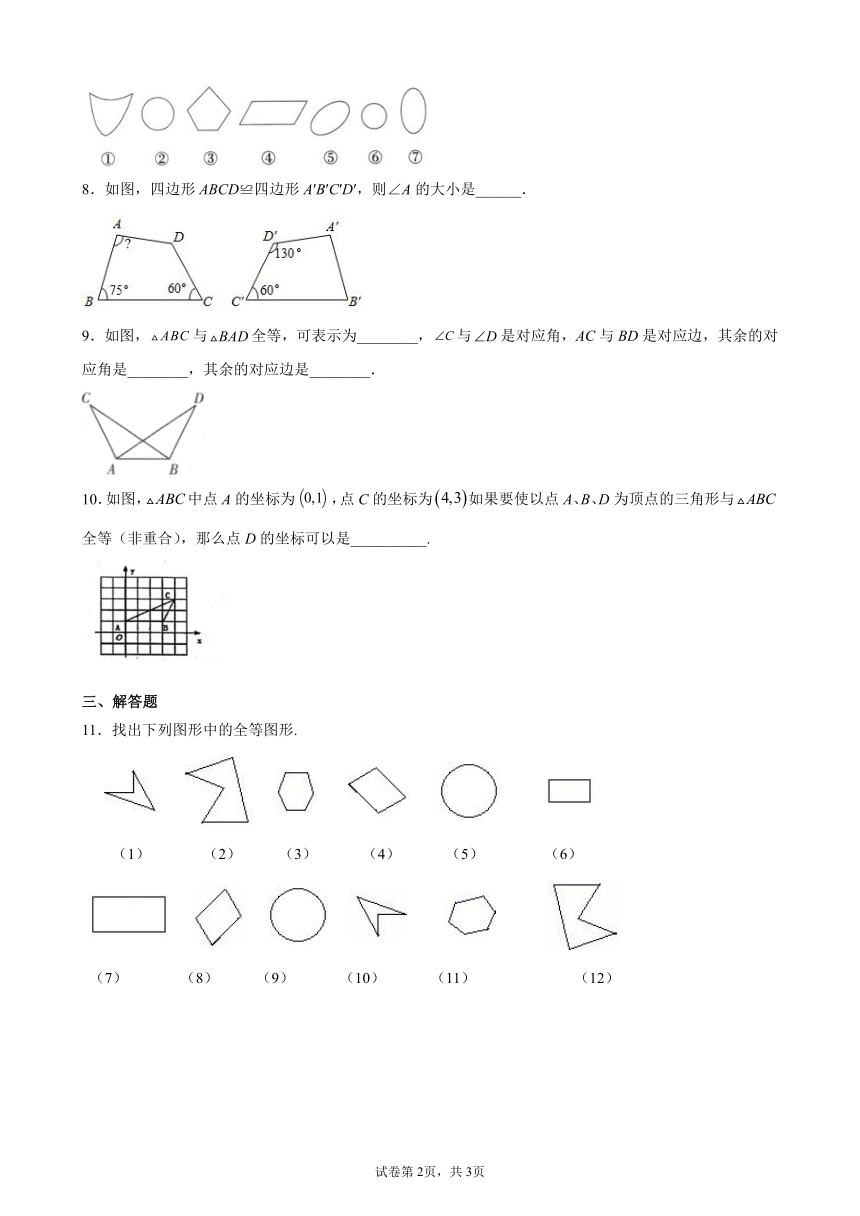
7.下列图形中是全等图形的是__________.(填序号)
8.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是______.
9.如图,与全等,可表示为________,与是对应角,AC与BD是对应边,其余的对应角是________,其余的对应边是________.
10.如图,中点A的坐标为,点C的坐标为如果要使以点A、B、D为顶点的三角形与全等(非重合),那么点D的坐标可以是__________.
三、解答题
11.找出下列图形中的全等图形.
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
12.找出图中全等的图形.
13.将一块正方形阴影划分为4个全等的部分.
14.如图,,和,和是对应边.写出其他对应边及对应角.
15.如图,若,与是对应角,与是对应边,写出其他的对应边及对应角.
试卷第2页,共3页
试卷第3页,共3页
参考答案
1.C
【解析】根据全等图形的概念“能够完全重合的两个图形叫做全等图形”可知,C中的两个图形是全等图形.
答案:C
易错:A
错因:只看到两个图形形状相同,图案相同,没注意大小不同.
满分备考:如果两个图形是全等图形,那么它们必然形状相同、大小相同,只是位置不同.
2.D
【解析】因为一个正方体展开会产生6个全等的正方形,所以有六个全等的正方形.
故选:D.
3.C
【解析】由图可知:(a)、(b)、(d)的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.
故选:.
4.A
【解析】根据全等的直角三角形的性质依次分析各小题即可判断.
用两个全等的直角三角形一定可以拼成平行四边形、矩形、等腰三角形
故选A.
5.C
【解析】解:A、形状相同的两个三角形全等,说法错误,本选项不符合题意;
B、面积相等的两个三角形全等,说法错误,本选项不符合题意;
C、完全重合的两个三角形全等,说法正确,本选项符合题意;
D、所有的等腰三角形都全等,说法错误,本选项不符合题意.
故选 :C.
6.C
【解析】∵ABC≌△CDA,∠BAC=∠DCA,
∴∠BAC与∠DCA是对应角,
∴BC与DA是对应边(对应角对的边是对应边).
故选C.
7.⑤和⑦
【解析】解:由全等形的定义可知:⑤和⑦是全等图形,
故答案为:⑤和⑦.
8.95°
【解析】∵四边形ABCD≌四边形A′B′C′D′
∴∠D=∠D′=130゜
∵四边形ABCD的内角和为360゜
∴∠A=360゜-∠B-∠C-∠D=95゜
故答案为:95゜
9. 与,与 AB与BA,BC与AD
【解析】解:,与是对应角,AC与BD是对应边,
其余的对应角是与,与;
其余的对应边是AB与BA,BC与AD.
故答案为:,与,与,AB与BA,BC与AD
10.或或
【解析】如图,
∵与有一条公共边AB,
当点D在边AB上方时,坐标为
当点D在边AB下方时,坐标为或
故答案为:或或.
11.(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形
【解析】根据全等图形的概念,可知:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.
12.见解答过程.
【解析】如图所示:1和2全等,3和4全等.
13.见解析.
【解析】如图划分
14.其他对应边:和.对应角:和,和,和.
【解析】解:∵△ABC≌△CDA,
∴其他对应边:AC和CA.对应角:∠BAC和∠DCA,∠B和∠D,∠ACB和∠CAD.
15.与是对应边,与是对应边,与是对应角,与是对应角.
【解析】解:因为,
所以与是对应边,
与是对应边,
与是对应角,
与是对应角.
答案第4页,共1页
答案第3页,共3页
4.2图形的全等-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列各组图形中,是全等图形的是( )
A. B. C. D.
2.一个正方体的展开图有( )个全等的正方形.
A.2个 B.3个 C.4个 D.6个
3.如图,下面4个正方形的边长都相等,其中阴影部分的面积相等的图形有( )
A.0个 B.2个 C.3个 D.4个
4.用两个全等的直角三角形拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)正方形;(4)等腰三角形,一定可以拼成的图形是 ( )
A.(1)(2)(4) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(3)
5.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等
C.完全重合的两个三角形全等 D.所有的等腰三角形都全等
6.如图,,,则的对应边是( )
A. B. C. D.
二、填空题
7.下列图形中是全等图形的是__________.(填序号)
8.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是______.
9.如图,与全等,可表示为________,与是对应角,AC与BD是对应边,其余的对应角是________,其余的对应边是________.
10.如图,中点A的坐标为,点C的坐标为如果要使以点A、B、D为顶点的三角形与全等(非重合),那么点D的坐标可以是__________.
三、解答题
11.找出下列图形中的全等图形.
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
12.找出图中全等的图形.
13.将一块正方形阴影划分为4个全等的部分.
14.如图,,和,和是对应边.写出其他对应边及对应角.
15.如图,若,与是对应角,与是对应边,写出其他的对应边及对应角.
试卷第2页,共3页
试卷第3页,共3页
参考答案
1.C
【解析】根据全等图形的概念“能够完全重合的两个图形叫做全等图形”可知,C中的两个图形是全等图形.
答案:C
易错:A
错因:只看到两个图形形状相同,图案相同,没注意大小不同.
满分备考:如果两个图形是全等图形,那么它们必然形状相同、大小相同,只是位置不同.
2.D
【解析】因为一个正方体展开会产生6个全等的正方形,所以有六个全等的正方形.
故选:D.
3.C
【解析】由图可知:(a)、(b)、(d)的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.
故选:.
4.A
【解析】根据全等的直角三角形的性质依次分析各小题即可判断.
用两个全等的直角三角形一定可以拼成平行四边形、矩形、等腰三角形
故选A.
5.C
【解析】解:A、形状相同的两个三角形全等,说法错误,本选项不符合题意;
B、面积相等的两个三角形全等,说法错误,本选项不符合题意;
C、完全重合的两个三角形全等,说法正确,本选项符合题意;
D、所有的等腰三角形都全等,说法错误,本选项不符合题意.
故选 :C.
6.C
【解析】∵ABC≌△CDA,∠BAC=∠DCA,
∴∠BAC与∠DCA是对应角,
∴BC与DA是对应边(对应角对的边是对应边).
故选C.
7.⑤和⑦
【解析】解:由全等形的定义可知:⑤和⑦是全等图形,
故答案为:⑤和⑦.
8.95°
【解析】∵四边形ABCD≌四边形A′B′C′D′
∴∠D=∠D′=130゜
∵四边形ABCD的内角和为360゜
∴∠A=360゜-∠B-∠C-∠D=95゜
故答案为:95゜
9. 与,与 AB与BA,BC与AD
【解析】解:,与是对应角,AC与BD是对应边,
其余的对应角是与,与;
其余的对应边是AB与BA,BC与AD.
故答案为:,与,与,AB与BA,BC与AD
10.或或
【解析】如图,
∵与有一条公共边AB,
当点D在边AB上方时,坐标为
当点D在边AB下方时,坐标为或
故答案为:或或.
11.(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形
【解析】根据全等图形的概念,可知:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.
12.见解答过程.
【解析】如图所示:1和2全等,3和4全等.
13.见解析.
【解析】如图划分
14.其他对应边:和.对应角:和,和,和.
【解析】解:∵△ABC≌△CDA,
∴其他对应边:AC和CA.对应角:∠BAC和∠DCA,∠B和∠D,∠ACB和∠CAD.
15.与是对应边,与是对应边,与是对应角,与是对应角.
【解析】解:因为,
所以与是对应边,
与是对应边,
与是对应角,
与是对应角.
答案第4页,共1页
答案第3页,共3页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
