北师大版2021-2022年初中数学七年级下册4.3探索三角形全等的条件课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学七年级下册4.3探索三角形全等的条件课堂练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 20:06:52 | ||
图片预览




文档简介
2021-2022年初中数学七年级下册同步(北师大版)
4.3探索三角形全等的条件-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B.
C. D.
2.如图,用直尺和圆规作一个角等于已知角,能得出∠A′O′B′=∠AOB的依据是( )
A.SSS B.SAS C.ASA D.AAS
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ).
A.带①去 B.带②去 C.带③去 D.①②③都带
4.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS B.ASA C.AAS D.SSS
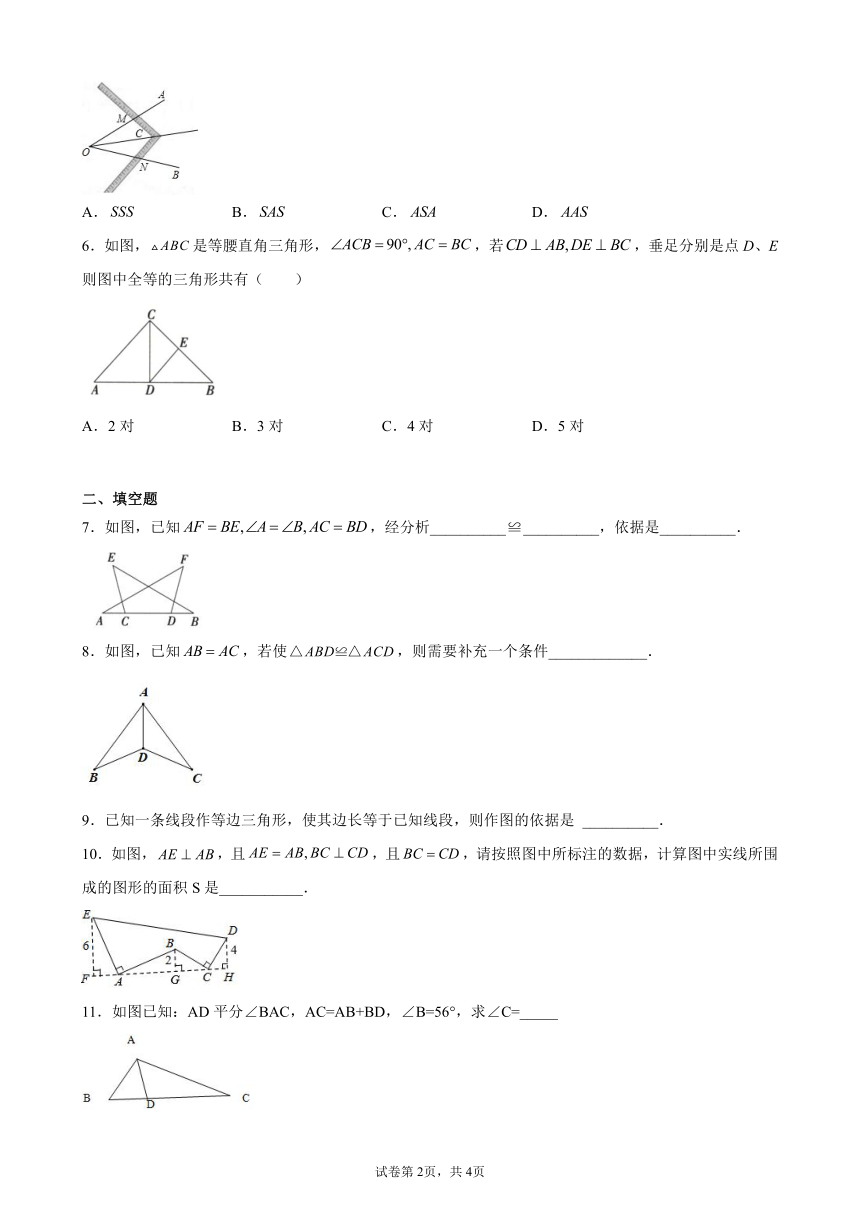
5.工人常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分别与点、重合,过角尺顶点作射线,由此作法便可得,共依据是( )
A. B. C. D.
6.如图,是等腰直角三角形,,若,垂足分别是点D、E则图中全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
二、填空题
7.如图,已知,经分析____________________,依据是__________.
8.如图,已知,若使,则需要补充一个条件_____________.
9.已知一条线段作等边三角形,使其边长等于已知线段,则作图的依据是 __________.
10.如图,,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是___________.
11.如图已知:AD平分∠BAC,AC=AB+BD,∠B=56°,求∠C=_____
12.如图,已知中,,,将绕点顺时针方向旋转60°到的位置,连接,则的长为______.
三、解答题
13.图中有三个正方形,请你说出图中所有的全等三角形.
14.如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,BD=CD.求证:EB=FC.
15.如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试证明.
16.已知,,,.直线过点,交、于点、.
(1)若是中线,求证:;
(2)若,求证:.
17.在中,,,直线MN经过点C,且于D点,于E点.
(1)当直线MN绕点C旋转到图①的位置时,求证:;
(2)当直线MN绕点C旋转到图②、图③的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
18.在中,,,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足分别为E.F.
(1)如图所示,当直线l不与底边AB相交时,求证:.
(2)当直线l绕点C旋转到图(b)的位置时,猜想EF、AE、BF之间的关系,并证明.
(3)当直线l绕点C旋转到图(c)的位置时,猜想EF、AE、BF之间的关系,直接写出结论.
试卷第4页,共5页
试卷第5页,共5页
参考答案
1.C
【解析】解:A、∵,,,
∴,选项不符合题意;
B、∵,,,
∴,选项不符合题意;
C、∵由,,,
∴无法判定,选项符合题意;
D、∵,,,
∴,选项不符合题意.
故选:C.
2.A
【解析】作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′B′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′A′.
所以∠A′O′B′就是与∠AOB相等的角;
在△OCD与△O′C′D′,O′C′=OC,O′D′=OD,C′D′=CD,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选:A.
3.C
【解析】带③去,理由如下:
∵③中满足ASA的条件,
∴带③去,
故选C.
4.A
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
5.A
【解析】解:由作图过程可得MO=NO,NC=MC,
在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
6.A
【解析】∵,,,,
∴,
同理可证明.
故选A.
7.
【解析】证明:∵AC=BD,
∴AD=BC,
在△ADF和△BCE中
∵ ,
∴△ADF≌△BCE(SAS).
故答案为:①,②,③.
8.BD=CD或∠BAD=∠CAD
【解析】解:若补充条件BD=CD,则可用SSS判定其全等;若添加∠BAD=∠CAD,则可用SAS判定其全等.
需补充的一个条件是BD=CD或∠BAD=∠CAD.
故答案为:BD=CD或∠BAD=∠CAD.
9.SSS
【解析】解::等边三角形三边相等,依题意得使其边长等于已知线段,则按全等三角形的判定定理(SSS)可得作图.
10.50
【解析】解:∵AE⊥AB,EF⊥AF,BG⊥AG,
∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△FEA和△GAB中,
∵,
∴△FEA≌△GAB(AAS),
∴AG=EF=6,AF=BG=2,
同理CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,
∴梯形EFHD的面积是×(EF+DH)×FH=×(6+4)×14=70,
∴阴影部分的面积是S梯形EFHD-S△EFA-S△ABC-S△DHC
=70-×6×2-×(6+4)×2-×4×2
=50.
故答案为50.
11.31°.
【解析】如图,在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
而AD是公共边,
∴△ABD≌△ADE,
∴∠B=∠AED=62°,DE=BD,
而AB+BD=AC=AE+CE,
∴DE=CE,
∴∠EDC=∠C,
而∠AED=∠C+∠EDC=62°,
∴∠C=31°.
12.2-2
【解析】解:如图,连接BB′,延长BC′交AB′于点M,
由题意得:∠BAB′=60°,BA=B′A,
∴△ABB′为等边三角形,
∴∠ABB′=60°,AB=B′B;
在△ABC′与△B′BC′中,
,
∴△ABC′≌△B′BC′(SSS),
∴∠MBB′=∠MBA=30°,
∴BM⊥AB′,且AM=B′M;
由题意得:,AB2=AC2+BC2=16,
∴AB′=AB=4,AM=2,
∴C′M=AB′=2;由勾股定理可求:BM=2,
∴C′B=2-2.
故答案为:2-2.
13.见解析.
【解析】解:如图:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAC=∠BCA=∠ACD=∠CAD=45°,
∴△ABC≌△CDA;
∵四边形EFGH是正方形,
∴EF=GH,∠EAF=∠EFA=∠HGC=∠HCG=45°,
∴△AEF≌△GHC;
∵四边形BPMN是正方形,
同理可得△ANM≌△CPM;
∴图中所有的全等三角形有3对,分别是△ANM≌△CPM;△AEF≌△GHC;△ABC≌△CDA.
14.见解析
【解析】证明:∵AD是∠BAC的角平分线DE⊥AB,DF⊥AC ,
∴DE=DF,∠DEB=∠DFC=90°,
∴ △BDE与△CDF 是直角三角形.
在 Rt△BDE 与 Rt△CDF 中
∵
∴ Rt△BDE≌ Rt△CDF (HL).
∴ BE=CF .
15.△ABC≌△AED,证明见解析.
【解析】解:△ABC≌△AED.
证明:∵BD=CE,
∴BC+CD=CD+DE,
即BC=ED.
在△ABC与△AED中,
∴△ABC≌△AED(SSS)
16.(1)详见解析;(2)详见解析.
【解析】解:(1)如图,延长至,使,
∵是中线,∴.
在和中,,
∴≌(SAS).∴,.
∵,∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(SAS).∴.
∵,∴.∴.
在中,,∴.
(2)如图,过点作交的延长线于,则,
∵,∴.
∵,∴.∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(AAS).∴.
∵,∴.
在和中,,
∴≌(AAS).∴.
17.(1)证明见解析,(2)图②中DE、AD、BE的等量关系是DE=AD﹣BE,图③中DE、AD、BE的等量关系是DE=BE﹣AD.
【解析】解:(1)①证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
∴△ADC≌△CEB(AAS).
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴DE=AD+BE.
(2)图②中DE、AD、BE的等量关系是DE=AD﹣BE,图③中DE、AD、BE的等量关系是DE=BE﹣AD.
如图②
∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
DE=AD﹣BE,
如图③
∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
18.(1)证明见解析;(2),理由见解析;(3).
【解析】证明:(1)∵,
∴,.
∵,
∴,
∴.
∵在和中,
,
∴.
∴.
∵,
∴.
(2),理由如下
∵,
∴,,
∵,
∴,
∴.
在和中,
,
∴.
∴,,
∵,
∴.
(3),理由如下
∵,
∴,,
∵,
∴,
∴.
在和中,
,
∴.
∴,,
∵,
∴.
答案第10页,共10页
答案第11页,共1页
4.3探索三角形全等的条件-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B.
C. D.
2.如图,用直尺和圆规作一个角等于已知角,能得出∠A′O′B′=∠AOB的依据是( )
A.SSS B.SAS C.ASA D.AAS
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ).
A.带①去 B.带②去 C.带③去 D.①②③都带
4.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS B.ASA C.AAS D.SSS
5.工人常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分别与点、重合,过角尺顶点作射线,由此作法便可得,共依据是( )
A. B. C. D.
6.如图,是等腰直角三角形,,若,垂足分别是点D、E则图中全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
二、填空题
7.如图,已知,经分析____________________,依据是__________.
8.如图,已知,若使,则需要补充一个条件_____________.
9.已知一条线段作等边三角形,使其边长等于已知线段,则作图的依据是 __________.
10.如图,,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是___________.
11.如图已知:AD平分∠BAC,AC=AB+BD,∠B=56°,求∠C=_____
12.如图,已知中,,,将绕点顺时针方向旋转60°到的位置,连接,则的长为______.
三、解答题
13.图中有三个正方形,请你说出图中所有的全等三角形.
14.如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,BD=CD.求证:EB=FC.
15.如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试证明.
16.已知,,,.直线过点,交、于点、.
(1)若是中线,求证:;
(2)若,求证:.
17.在中,,,直线MN经过点C,且于D点,于E点.
(1)当直线MN绕点C旋转到图①的位置时,求证:;
(2)当直线MN绕点C旋转到图②、图③的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
18.在中,,,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足分别为E.F.
(1)如图所示,当直线l不与底边AB相交时,求证:.
(2)当直线l绕点C旋转到图(b)的位置时,猜想EF、AE、BF之间的关系,并证明.
(3)当直线l绕点C旋转到图(c)的位置时,猜想EF、AE、BF之间的关系,直接写出结论.
试卷第4页,共5页
试卷第5页,共5页
参考答案
1.C
【解析】解:A、∵,,,
∴,选项不符合题意;
B、∵,,,
∴,选项不符合题意;
C、∵由,,,
∴无法判定,选项符合题意;
D、∵,,,
∴,选项不符合题意.
故选:C.
2.A
【解析】作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′B′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′A′.
所以∠A′O′B′就是与∠AOB相等的角;
在△OCD与△O′C′D′,O′C′=OC,O′D′=OD,C′D′=CD,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选:A.
3.C
【解析】带③去,理由如下:
∵③中满足ASA的条件,
∴带③去,
故选C.
4.A
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
5.A
【解析】解:由作图过程可得MO=NO,NC=MC,
在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
6.A
【解析】∵,,,,
∴,
同理可证明.
故选A.
7.
【解析】证明:∵AC=BD,
∴AD=BC,
在△ADF和△BCE中
∵ ,
∴△ADF≌△BCE(SAS).
故答案为:①,②,③.
8.BD=CD或∠BAD=∠CAD
【解析】解:若补充条件BD=CD,则可用SSS判定其全等;若添加∠BAD=∠CAD,则可用SAS判定其全等.
需补充的一个条件是BD=CD或∠BAD=∠CAD.
故答案为:BD=CD或∠BAD=∠CAD.
9.SSS
【解析】解::等边三角形三边相等,依题意得使其边长等于已知线段,则按全等三角形的判定定理(SSS)可得作图.
10.50
【解析】解:∵AE⊥AB,EF⊥AF,BG⊥AG,
∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△FEA和△GAB中,
∵,
∴△FEA≌△GAB(AAS),
∴AG=EF=6,AF=BG=2,
同理CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,
∴梯形EFHD的面积是×(EF+DH)×FH=×(6+4)×14=70,
∴阴影部分的面积是S梯形EFHD-S△EFA-S△ABC-S△DHC
=70-×6×2-×(6+4)×2-×4×2
=50.
故答案为50.
11.31°.
【解析】如图,在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
而AD是公共边,
∴△ABD≌△ADE,
∴∠B=∠AED=62°,DE=BD,
而AB+BD=AC=AE+CE,
∴DE=CE,
∴∠EDC=∠C,
而∠AED=∠C+∠EDC=62°,
∴∠C=31°.
12.2-2
【解析】解:如图,连接BB′,延长BC′交AB′于点M,
由题意得:∠BAB′=60°,BA=B′A,
∴△ABB′为等边三角形,
∴∠ABB′=60°,AB=B′B;
在△ABC′与△B′BC′中,
,
∴△ABC′≌△B′BC′(SSS),
∴∠MBB′=∠MBA=30°,
∴BM⊥AB′,且AM=B′M;
由题意得:,AB2=AC2+BC2=16,
∴AB′=AB=4,AM=2,
∴C′M=AB′=2;由勾股定理可求:BM=2,
∴C′B=2-2.
故答案为:2-2.
13.见解析.
【解析】解:如图:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAC=∠BCA=∠ACD=∠CAD=45°,
∴△ABC≌△CDA;
∵四边形EFGH是正方形,
∴EF=GH,∠EAF=∠EFA=∠HGC=∠HCG=45°,
∴△AEF≌△GHC;
∵四边形BPMN是正方形,
同理可得△ANM≌△CPM;
∴图中所有的全等三角形有3对,分别是△ANM≌△CPM;△AEF≌△GHC;△ABC≌△CDA.
14.见解析
【解析】证明:∵AD是∠BAC的角平分线DE⊥AB,DF⊥AC ,
∴DE=DF,∠DEB=∠DFC=90°,
∴ △BDE与△CDF 是直角三角形.
在 Rt△BDE 与 Rt△CDF 中
∵
∴ Rt△BDE≌ Rt△CDF (HL).
∴ BE=CF .
15.△ABC≌△AED,证明见解析.
【解析】解:△ABC≌△AED.
证明:∵BD=CE,
∴BC+CD=CD+DE,
即BC=ED.
在△ABC与△AED中,
∴△ABC≌△AED(SSS)
16.(1)详见解析;(2)详见解析.
【解析】解:(1)如图,延长至,使,
∵是中线,∴.
在和中,,
∴≌(SAS).∴,.
∵,∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(SAS).∴.
∵,∴.∴.
在中,,∴.
(2)如图,过点作交的延长线于,则,
∵,∴.
∵,∴.∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(AAS).∴.
∵,∴.
在和中,,
∴≌(AAS).∴.
17.(1)证明见解析,(2)图②中DE、AD、BE的等量关系是DE=AD﹣BE,图③中DE、AD、BE的等量关系是DE=BE﹣AD.
【解析】解:(1)①证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
∴△ADC≌△CEB(AAS).
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴DE=AD+BE.
(2)图②中DE、AD、BE的等量关系是DE=AD﹣BE,图③中DE、AD、BE的等量关系是DE=BE﹣AD.
如图②
∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
DE=AD﹣BE,
如图③
∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
18.(1)证明见解析;(2),理由见解析;(3).
【解析】证明:(1)∵,
∴,.
∵,
∴,
∴.
∵在和中,
,
∴.
∴.
∵,
∴.
(2),理由如下
∵,
∴,,
∵,
∴,
∴.
在和中,
,
∴.
∴,,
∵,
∴.
(3),理由如下
∵,
∴,,
∵,
∴,
∴.
在和中,
,
∴.
∴,,
∵,
∴.
答案第10页,共10页
答案第11页,共1页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
