人教版2021-2022年初中数学七年级下册5.1.2垂线 课堂练习(Word版含答案)
文档属性
| 名称 | 人教版2021-2022年初中数学七年级下册5.1.2垂线 课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 299.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 00:00:00 | ||
图片预览


文档简介
2021-2022年初中数学七年级下册同步(人教版)
5.1.2垂线-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
2.如图,直线AB、CD相交于O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
3.过直线l上一点A,在同一平面内画直线l的垂线,可以画的条数是( )
A.无数条 B.1 C.2 D.不能确定
4.如图,点P是直线a外的一点,点A,B,C在直线a上,且PB⊥a于B,PA⊥PC,则下列错误语句是( )
A.线段PB的长是点P到直线a的距离 B.PA,PB,PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离 D.线段PC的长是点C到直线PA的距离
5.如图,体育课上测量跳远成绩的依据是( )
A.平行线间的距离相等 B.两点之间,线段最短
C.垂线段最短 D.两点确定一条直线
6.若直线a与直线b相交于点A,则直线b上到直线a距离等于5cm的点的个数是( ).
A.0 B.1 C.2 D.3
二、填空题
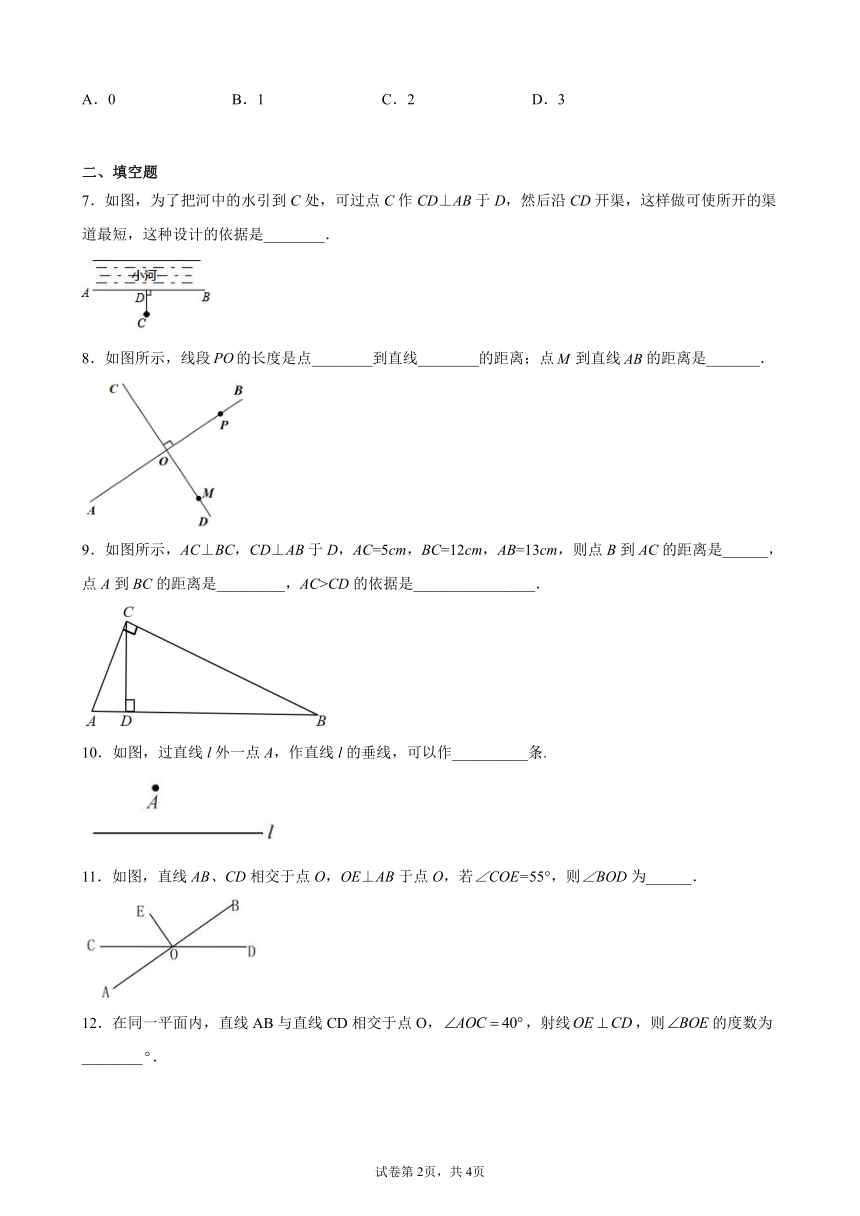
7.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是________.
8.如图所示,线段的长度是点________到直线________的距离;点到直线的距离是_______.
9.如图所示,AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是______,点A到BC的距离是_________,AC>CD的依据是________________.
10.如图,过直线l外一点A,作直线l的垂线,可以作__________条.
11.如图,直线AB、CD相交于点O,OE⊥AB于点O,若∠COE=55°,则∠BOD为______.
12.在同一平面内,直线AB与直线CD相交于点O,,射线,则的度数为________.
三、解答题
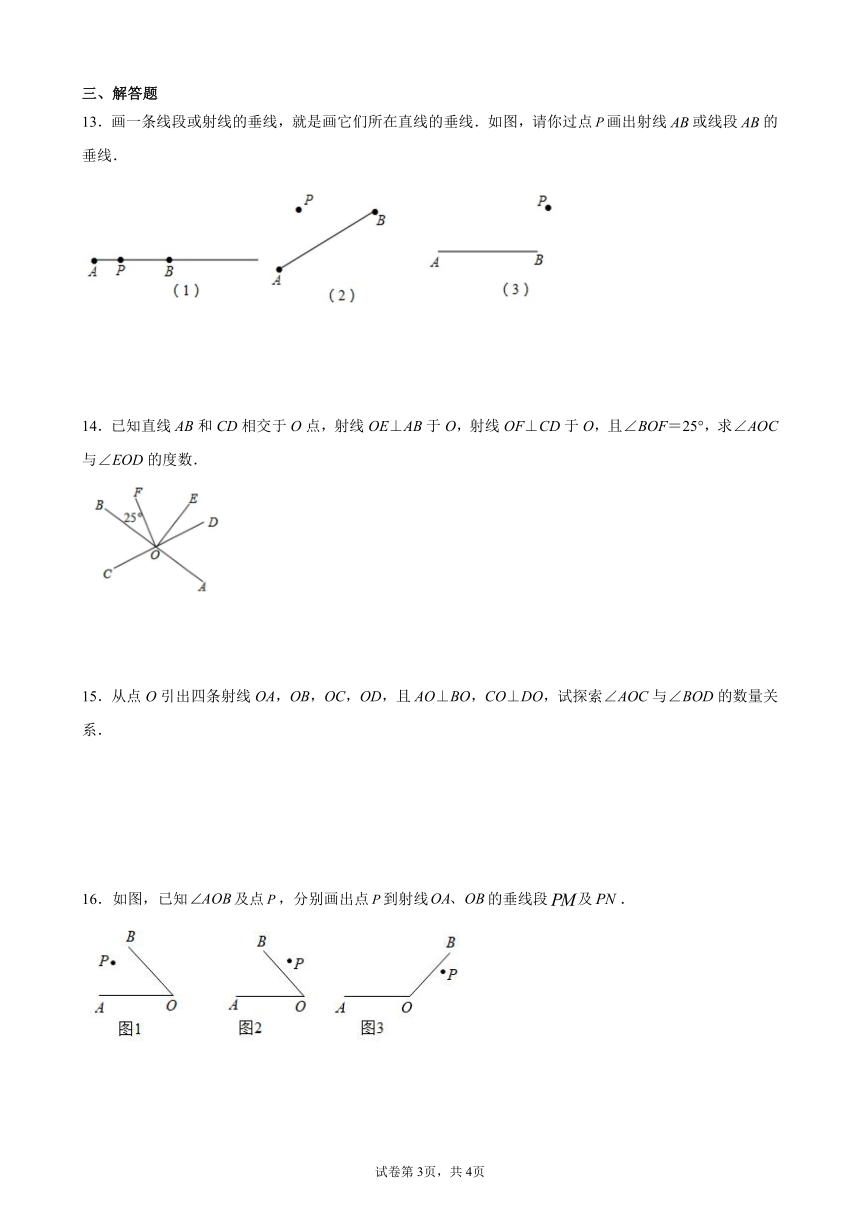
13.画一条线段或射线的垂线,就是画它们所在直线的垂线.如图,请你过点画出射线或线段的垂线.
14.已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°,求∠AOC与∠EOD的度数.
15.从点O引出四条射线OA,OB,OC,OD,且AO⊥BO,CO⊥DO,试探索∠AOC与∠BOD的数量关系.
16.如图,已知及点,分别画出点到射线的垂线段及.
17.如图.
(1)试说出点A到直线BC的距离;点B到直线AC的距离;
(2)点C到直线AB的距离是多少?
18.如图,三角形中,.
(1)分别指出点到直线,点到直线的距离是哪些线段的长;
(2)三条边,,中哪条边最长?为什么?
试卷第4页,共4页
试卷第3页,共4页
参考答案
1.B
【解析】解:根据垂线的性质,这样的直线只能作一条,
故选:B.
2.C
【解析】解:∵射线OM平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON-∠MOC=90°-35°=55°.
故选:C.
3.B
【解析】根据垂线的性质,这样的直线只能作一条,
故选B.
4.C
【解析】解:A、根据点到直线的距离的定义:即点到这一直线的垂线段的长度.故此选项正确;
B、根据垂线段最短可知此选项正确;
C、线段AP的长是点A到直线PC的距离,故选项错误;
D、根据点到直线的距离即点到这一直线的垂线段的长度.故此选项正确.
故选:C.
5.C
【解析】体育课上测量跳远成绩是:落地时脚跟所在点到起跳线的距离,依据的是垂线段最短
故选:C.
6.C
【解析】解:直线b上的点P和Q到直线a距离等于5cm的点有B和C两个,
故选:C.
7.垂线段最短
【解析】解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短.
故答案为:垂线段最短.
8.P 线段的长
【解析】解:线段的长度是点P到直线的距离;点到直线的距离是线段的长,
故答案为:P,,线段的长.
9. 垂线段最短
【解析】解:∵AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,
∴B到AC的距离是12cm,A点到BC的距离是5cm,
∵垂线段最短,
∴CD<AC,
故答案为:12cm,5cm,垂线段最短.
10.1
【解析】过直线l外一点A,作直线l的垂线,可以作1条.
故答案为1.
11.35°
【解析】解:∵OE⊥AB,
∴∠AOE=90°,
∵ ,
∴∠AOC=90°- ,
∴∠BOD=∠AOC= ,
故答案为:35°.
12.50°或130°
【解析】解:如图1:
∵OE⊥CD,
∴∠DOE=90°,
∵,
∴∠DOB=°,
∴∠BOE=90°-40°=50°,
如图2:
∵OE⊥CD,
∴∠DOE =90°,
∵,
∴∠DOB=°,
∴∠BOE=90°+40°=130°,
故答案为:50°或130°.
13.见详解
【解析】如图所示:
(1)PQ即为所求;
(2)PM即为所求;
(3)PN即为所求.
14.∠AOC=115°,∠EOD=25°
【解析】解:∵OF⊥CD,
∴∠DOF=90°,
又∵∠BOF=25°,
∴∠BOD=∠DOF+∠BOF=90°+25°=115°,
∴∠AOC=∠BOD=115°,
又∵OE⊥AB,
∴∠BOE=90°,
∵∠BOF=25°,
∴∠EOF=∠BOE -∠BOF =65°,
∴∠EOD=∠DOF﹣∠EOF=90°-65°=25°.
15.相等或互补
【解析】解:①如图①所示:
∵∠AOC+∠BOC=∠BOD+∠BOC=90°,
∴∠AOC=∠BOD;
②如图②所示:
∵∠AOC+∠BOA+∠BOD+∠DOC=360°,
即∠AOC+90°+∠BOD+90°=360°,
∴∠AOC+∠BOD=180°.
综上,∠AOC与∠BOD的数量关系是:相等或互补.
16.作图见解析
【解析】解:利用直角三角形的一边分别与射线OA、OB所在的直线重合,另一边过点P作图可得:
17.(1)点A到直线BC的距离、点B到直线AC的距离分别是9,12;(2)
【解析】(1)∵,
∴点A到直线BC的距离、点B到直线AC的距离分别是9,12.
(2)设点C到直线AB的距离为h,
的面积为,
∴,
∴.
∴点C到直线AB的距离为.
18.(1)点到直线的距离为线段的长,点到直线的距离为线段的长;(2)根据“垂线段最短”,可知线段最长.
【解析】解:(1)∵,
∴,
∴点到直线的距离为线段的长,点到直线的距离为线段的长;
(2)由点到直线的距离,垂线段的长度最短可知:,,
∴三条边,,中最长的边为.
答案第6页,共1页
答案第5页,共5页
5.1.2垂线-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
2.如图,直线AB、CD相交于O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
3.过直线l上一点A,在同一平面内画直线l的垂线,可以画的条数是( )
A.无数条 B.1 C.2 D.不能确定
4.如图,点P是直线a外的一点,点A,B,C在直线a上,且PB⊥a于B,PA⊥PC,则下列错误语句是( )
A.线段PB的长是点P到直线a的距离 B.PA,PB,PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离 D.线段PC的长是点C到直线PA的距离
5.如图,体育课上测量跳远成绩的依据是( )
A.平行线间的距离相等 B.两点之间,线段最短
C.垂线段最短 D.两点确定一条直线
6.若直线a与直线b相交于点A,则直线b上到直线a距离等于5cm的点的个数是( ).
A.0 B.1 C.2 D.3
二、填空题
7.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是________.
8.如图所示,线段的长度是点________到直线________的距离;点到直线的距离是_______.
9.如图所示,AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是______,点A到BC的距离是_________,AC>CD的依据是________________.
10.如图,过直线l外一点A,作直线l的垂线,可以作__________条.
11.如图,直线AB、CD相交于点O,OE⊥AB于点O,若∠COE=55°,则∠BOD为______.
12.在同一平面内,直线AB与直线CD相交于点O,,射线,则的度数为________.
三、解答题
13.画一条线段或射线的垂线,就是画它们所在直线的垂线.如图,请你过点画出射线或线段的垂线.
14.已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°,求∠AOC与∠EOD的度数.
15.从点O引出四条射线OA,OB,OC,OD,且AO⊥BO,CO⊥DO,试探索∠AOC与∠BOD的数量关系.
16.如图,已知及点,分别画出点到射线的垂线段及.
17.如图.
(1)试说出点A到直线BC的距离;点B到直线AC的距离;
(2)点C到直线AB的距离是多少?
18.如图,三角形中,.
(1)分别指出点到直线,点到直线的距离是哪些线段的长;
(2)三条边,,中哪条边最长?为什么?
试卷第4页,共4页
试卷第3页,共4页
参考答案
1.B
【解析】解:根据垂线的性质,这样的直线只能作一条,
故选:B.
2.C
【解析】解:∵射线OM平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON-∠MOC=90°-35°=55°.
故选:C.
3.B
【解析】根据垂线的性质,这样的直线只能作一条,
故选B.
4.C
【解析】解:A、根据点到直线的距离的定义:即点到这一直线的垂线段的长度.故此选项正确;
B、根据垂线段最短可知此选项正确;
C、线段AP的长是点A到直线PC的距离,故选项错误;
D、根据点到直线的距离即点到这一直线的垂线段的长度.故此选项正确.
故选:C.
5.C
【解析】体育课上测量跳远成绩是:落地时脚跟所在点到起跳线的距离,依据的是垂线段最短
故选:C.
6.C
【解析】解:直线b上的点P和Q到直线a距离等于5cm的点有B和C两个,
故选:C.
7.垂线段最短
【解析】解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短.
故答案为:垂线段最短.
8.P 线段的长
【解析】解:线段的长度是点P到直线的距离;点到直线的距离是线段的长,
故答案为:P,,线段的长.
9. 垂线段最短
【解析】解:∵AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,
∴B到AC的距离是12cm,A点到BC的距离是5cm,
∵垂线段最短,
∴CD<AC,
故答案为:12cm,5cm,垂线段最短.
10.1
【解析】过直线l外一点A,作直线l的垂线,可以作1条.
故答案为1.
11.35°
【解析】解:∵OE⊥AB,
∴∠AOE=90°,
∵ ,
∴∠AOC=90°- ,
∴∠BOD=∠AOC= ,
故答案为:35°.
12.50°或130°
【解析】解:如图1:
∵OE⊥CD,
∴∠DOE=90°,
∵,
∴∠DOB=°,
∴∠BOE=90°-40°=50°,
如图2:
∵OE⊥CD,
∴∠DOE =90°,
∵,
∴∠DOB=°,
∴∠BOE=90°+40°=130°,
故答案为:50°或130°.
13.见详解
【解析】如图所示:
(1)PQ即为所求;
(2)PM即为所求;
(3)PN即为所求.
14.∠AOC=115°,∠EOD=25°
【解析】解:∵OF⊥CD,
∴∠DOF=90°,
又∵∠BOF=25°,
∴∠BOD=∠DOF+∠BOF=90°+25°=115°,
∴∠AOC=∠BOD=115°,
又∵OE⊥AB,
∴∠BOE=90°,
∵∠BOF=25°,
∴∠EOF=∠BOE -∠BOF =65°,
∴∠EOD=∠DOF﹣∠EOF=90°-65°=25°.
15.相等或互补
【解析】解:①如图①所示:
∵∠AOC+∠BOC=∠BOD+∠BOC=90°,
∴∠AOC=∠BOD;
②如图②所示:
∵∠AOC+∠BOA+∠BOD+∠DOC=360°,
即∠AOC+90°+∠BOD+90°=360°,
∴∠AOC+∠BOD=180°.
综上,∠AOC与∠BOD的数量关系是:相等或互补.
16.作图见解析
【解析】解:利用直角三角形的一边分别与射线OA、OB所在的直线重合,另一边过点P作图可得:
17.(1)点A到直线BC的距离、点B到直线AC的距离分别是9,12;(2)
【解析】(1)∵,
∴点A到直线BC的距离、点B到直线AC的距离分别是9,12.
(2)设点C到直线AB的距离为h,
的面积为,
∴,
∴.
∴点C到直线AB的距离为.
18.(1)点到直线的距离为线段的长,点到直线的距离为线段的长;(2)根据“垂线段最短”,可知线段最长.
【解析】解:(1)∵,
∴,
∴点到直线的距离为线段的长,点到直线的距离为线段的长;
(2)由点到直线的距离,垂线段的长度最短可知:,,
∴三条边,,中最长的边为.
答案第6页,共1页
答案第5页,共5页
