黑龙江省大庆市万宝学校2021-2022学年上学期九年级期中考试数学试题(word版含图片答案)
文档属性
| 名称 | 黑龙江省大庆市万宝学校2021-2022学年上学期九年级期中考试数学试题(word版含图片答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 16:04:34 | ||
图片预览

文档简介
大庆市万宝学校2021-2022学年九年级上学期期中考试
数学试题
考生注意∶1、考试时间∶120分钟2、全卷共三道大题,满分 120 分
选择题(共10小题,满分 30分,每小题3分)
1.(3分)下列函数中是二次函数的是( )
A.S=2t-3 B.y= C.y=x2 D. y=a2+bx+c
2.(3分)若 sinA=,则∠A的大小是( )
A.30° B.45° C. 60° D.90°
3.(3分)下列4个说法中;①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆∶正确的有( )
A.1个 B.2个 C.3个 D.4个
4.(3分)如图,在Rt△ABC中,BC=3,斜边AC=5,则下列等式正确的是()
A.SinC= B. cosC= C. tanA= D. SinA=
5.(3分)下列由实线组成的图形中,为半圆的是()
(3分)已知二次函数y=(a+1)x -对ta 2-1图象经过原点,则a的取值为( )
A.a=±1 B. a=1 C.a=-1 D.无法确定
7.(3分)在Rt△ABC中,各边都扩大10倍,则LA的三角函数值( )
A.不变 B.扩大10倍 C.缩小10倍 D.不能确定
8.(3分)已知抛物线y=x +bx+4经过(-4,n)和(4,n)两点,则b的值为()
A.-2 B.-4 C.0 D.4
9.(3分)如图,在半径为2的⊙O中,弦AB,CD互相垂直,垂足为点P.若AB=CD=8,则OP的长为( )
A.4 B. 2 C.4 D.2
第9题图 第10题图 第11题图
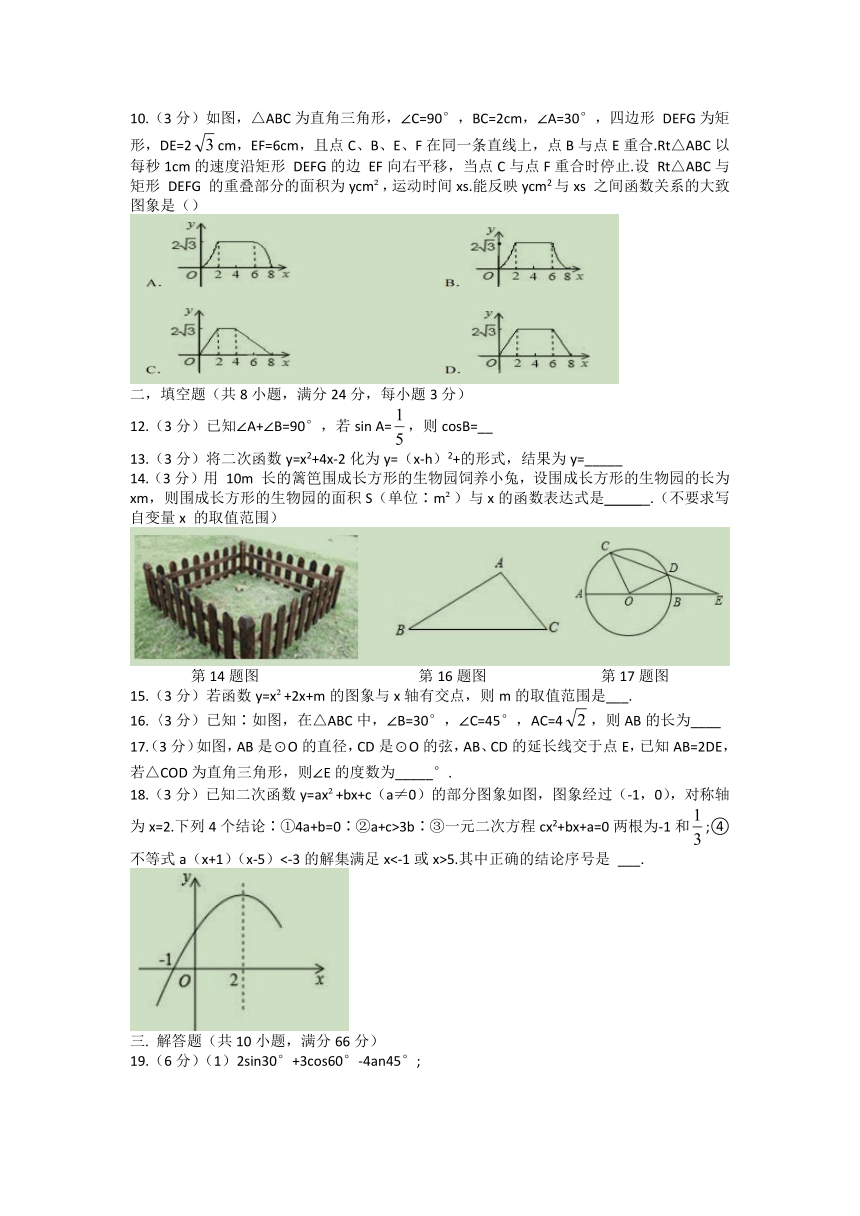
10.(3分)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形 DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形 DEFG的边 EF向右平移,当点C与点F重合时停止.设 Rt△ABC与矩形 DEFG 的重叠部分的面积为ycm ,运动时间xs.能反映ycm2与xs 之间函数关系的大致图象是()
二,填空题(共8小题,满分24分,每小题3分)
12.(3分)已知∠A+∠B=90°,若sin A=,则cosB=__
13.(3分)将二次函数y=x2+4x-2化为y=(x-h)2+的形式,结果为y=_____
14.(3分)用 10m 长的篱笆围成长方形的生物园饲养小兔,设围成长方形的生物园的长为xm,则围成长方形的生物园的面积S(单位∶m )与x的函数表达式是 _.(不要求写自变量x 的取值范围)
第14题图 第16题图 第17题图
15.(3分)若函数y=x +2x+m的图象与x轴有交点,则m的取值范围是___.
16.〈3分)已知∶如图,在△ABC中,∠B=30°,∠C=45°,AC=4,则AB的长为____
17.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,
若△COD为直角三角形,则∠E的度数为_____°.
18.(3分)已知二次函数y=ax +bx+c(a≠0)的部分图象如图,图象经过(-1,0),对称轴为x=2.下列4个结论∶①4a+b=0∶②a+c>3b∶③一元二次方程cx2+bx+a=0两根为-1和;④不等式a(x+1)(x-5)<-3的解集满足x<-1或x>5.其中正确的结论序号是 ___.
三. 解答题(共10小题,满分66分)
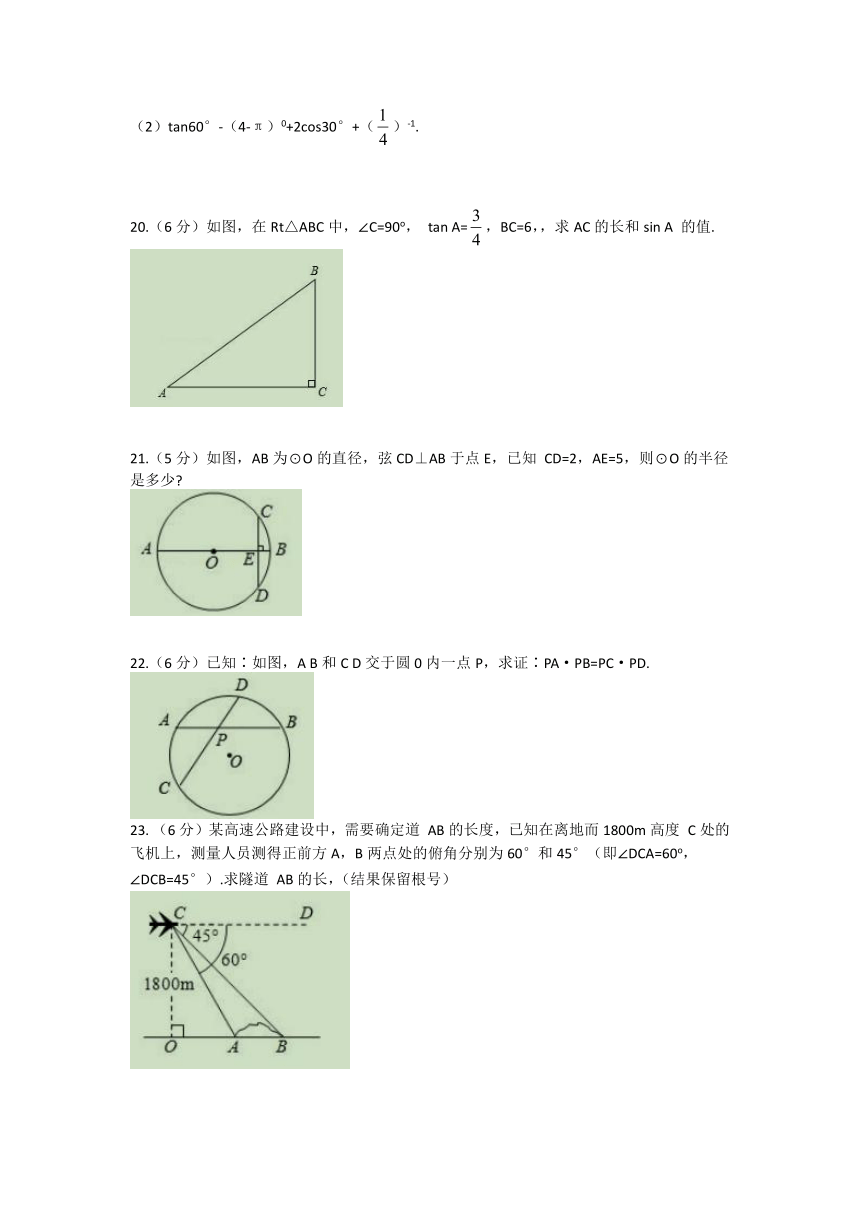
19.(6分)(1)2sin30°+3cos60°-4an45°;
tan60°-(4-π)0+2cos30°+()-1.
20.(6分)如图,在Rt△ABC中,∠C=90o, tan A=,BC=6,,求AC的长和sin A 的值.
21.(5分)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知 CD=2,AE=5,则⊙O的半径
是多少
22.(6分)已知∶如图,A B和C D交于圆0内一点P,求证∶PA·PB=PC·PD.
(6分)某高速公路建设中,需要确定道 AB的长度,已知在离地而1800m高度 C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°(即∠DCA=60o,
∠DCB=45°).求隧道 AB的长,(结果保留根号)
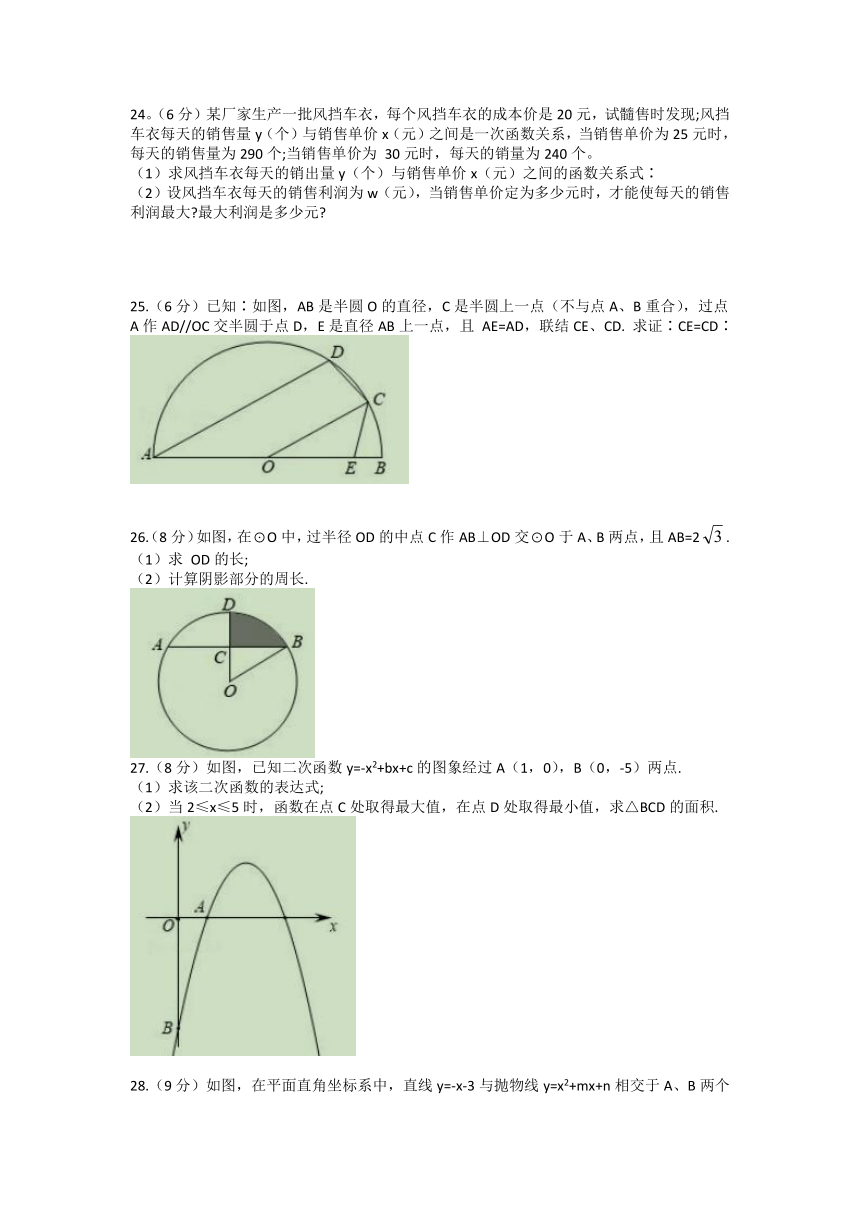
24。(6分)某厂家生产一批风挡车衣,每个风挡车衣的成本价是20元,试髓售时发现;风挡车衣每天的销售量y(个)与销售单价x(元)之间是一次函数关系,当销售单价为25元时,每天的销售量为290个;当销售单价为 30元时,每天的销量为240个。
(1)求风挡车衣每天的销出量y(个)与销售单价x(元)之间的函数关系式∶
(2)设风挡车衣每天的销售利润为w(元),当销售单价定为多少元时,才能使每天的销售利润最大 最大利润是多少元
25.(6分)已知∶如图,AB是半圆O的直径,C是半圆上一点(不与点A、B重合),过点A作AD//OC交半圆于点D,E是直径AB上一点,且 AE=AD,联结CE、CD. 求证∶CE=CD∶
26.(8分)如图,在⊙O中,过半径OD的中点C作AB⊥OD交⊙O于A、B两点,且AB=2.
(1)求 OD的长;
(2)计算阴影部分的周长.
27.(8分)如图,已知二次函数y=-x2+bx+c的图象经过A(1,0),B(0,-5)两点.
(1)求该二次函数的表达式;
(2)当2≤x≤5时,函数在点C处取得最大值,在点D处取得最小值,求△BCD的面积.
28.(9分)如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上。
(1)n=_____用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值∶
(3)①设 m=-2,当-3≤x≤0时,求二次函数y=x +mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
数学试题
考生注意∶1、考试时间∶120分钟2、全卷共三道大题,满分 120 分
选择题(共10小题,满分 30分,每小题3分)
1.(3分)下列函数中是二次函数的是( )
A.S=2t-3 B.y= C.y=x2 D. y=a2+bx+c
2.(3分)若 sinA=,则∠A的大小是( )
A.30° B.45° C. 60° D.90°
3.(3分)下列4个说法中;①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆∶正确的有( )
A.1个 B.2个 C.3个 D.4个
4.(3分)如图,在Rt△ABC中,BC=3,斜边AC=5,则下列等式正确的是()
A.SinC= B. cosC= C. tanA= D. SinA=
5.(3分)下列由实线组成的图形中,为半圆的是()
(3分)已知二次函数y=(a+1)x -对ta 2-1图象经过原点,则a的取值为( )
A.a=±1 B. a=1 C.a=-1 D.无法确定
7.(3分)在Rt△ABC中,各边都扩大10倍,则LA的三角函数值( )
A.不变 B.扩大10倍 C.缩小10倍 D.不能确定
8.(3分)已知抛物线y=x +bx+4经过(-4,n)和(4,n)两点,则b的值为()
A.-2 B.-4 C.0 D.4
9.(3分)如图,在半径为2的⊙O中,弦AB,CD互相垂直,垂足为点P.若AB=CD=8,则OP的长为( )
A.4 B. 2 C.4 D.2
第9题图 第10题图 第11题图
10.(3分)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形 DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形 DEFG的边 EF向右平移,当点C与点F重合时停止.设 Rt△ABC与矩形 DEFG 的重叠部分的面积为ycm ,运动时间xs.能反映ycm2与xs 之间函数关系的大致图象是()
二,填空题(共8小题,满分24分,每小题3分)
12.(3分)已知∠A+∠B=90°,若sin A=,则cosB=__
13.(3分)将二次函数y=x2+4x-2化为y=(x-h)2+的形式,结果为y=_____
14.(3分)用 10m 长的篱笆围成长方形的生物园饲养小兔,设围成长方形的生物园的长为xm,则围成长方形的生物园的面积S(单位∶m )与x的函数表达式是 _.(不要求写自变量x 的取值范围)
第14题图 第16题图 第17题图
15.(3分)若函数y=x +2x+m的图象与x轴有交点,则m的取值范围是___.
16.〈3分)已知∶如图,在△ABC中,∠B=30°,∠C=45°,AC=4,则AB的长为____
17.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,
若△COD为直角三角形,则∠E的度数为_____°.
18.(3分)已知二次函数y=ax +bx+c(a≠0)的部分图象如图,图象经过(-1,0),对称轴为x=2.下列4个结论∶①4a+b=0∶②a+c>3b∶③一元二次方程cx2+bx+a=0两根为-1和;④不等式a(x+1)(x-5)<-3的解集满足x<-1或x>5.其中正确的结论序号是 ___.
三. 解答题(共10小题,满分66分)
19.(6分)(1)2sin30°+3cos60°-4an45°;
tan60°-(4-π)0+2cos30°+()-1.
20.(6分)如图,在Rt△ABC中,∠C=90o, tan A=,BC=6,,求AC的长和sin A 的值.
21.(5分)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知 CD=2,AE=5,则⊙O的半径
是多少
22.(6分)已知∶如图,A B和C D交于圆0内一点P,求证∶PA·PB=PC·PD.
(6分)某高速公路建设中,需要确定道 AB的长度,已知在离地而1800m高度 C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°(即∠DCA=60o,
∠DCB=45°).求隧道 AB的长,(结果保留根号)
24。(6分)某厂家生产一批风挡车衣,每个风挡车衣的成本价是20元,试髓售时发现;风挡车衣每天的销售量y(个)与销售单价x(元)之间是一次函数关系,当销售单价为25元时,每天的销售量为290个;当销售单价为 30元时,每天的销量为240个。
(1)求风挡车衣每天的销出量y(个)与销售单价x(元)之间的函数关系式∶
(2)设风挡车衣每天的销售利润为w(元),当销售单价定为多少元时,才能使每天的销售利润最大 最大利润是多少元
25.(6分)已知∶如图,AB是半圆O的直径,C是半圆上一点(不与点A、B重合),过点A作AD//OC交半圆于点D,E是直径AB上一点,且 AE=AD,联结CE、CD. 求证∶CE=CD∶
26.(8分)如图,在⊙O中,过半径OD的中点C作AB⊥OD交⊙O于A、B两点,且AB=2.
(1)求 OD的长;
(2)计算阴影部分的周长.
27.(8分)如图,已知二次函数y=-x2+bx+c的图象经过A(1,0),B(0,-5)两点.
(1)求该二次函数的表达式;
(2)当2≤x≤5时,函数在点C处取得最大值,在点D处取得最小值,求△BCD的面积.
28.(9分)如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上。
(1)n=_____用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值∶
(3)①设 m=-2,当-3≤x≤0时,求二次函数y=x +mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
同课章节目录
