2022届高三冲刺高考 (文科数学)概率课件(共38张PPT)
文档属性
| 名称 | 2022届高三冲刺高考 (文科数学)概率课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 19:53:29 | ||
图片预览











文档简介
(共38张PPT)
冲刺高考(文科数学) 概率
考点一 古典概型——巧选方法,熟用公式
1.古典概型的概率公式
P(A)==.
2.古典概型的两个特点
(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件出现的可能性相等.
[例1] (1)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A. B.
C. D.
解析:从O,A,B,C,D中任取3点的情况有(O,A,B),(O,A,C),(O,A,D),(O,B,C),(O,B,D),(O,C,D),(A,B,C),(A,B,D),(B,C,D),(A,C,D),共有10种不同的情况,由图可知取到的3点共线的有(O,A,C)和(O,B,D)两种情况,所以所求概率为=.故选A.
答案:A
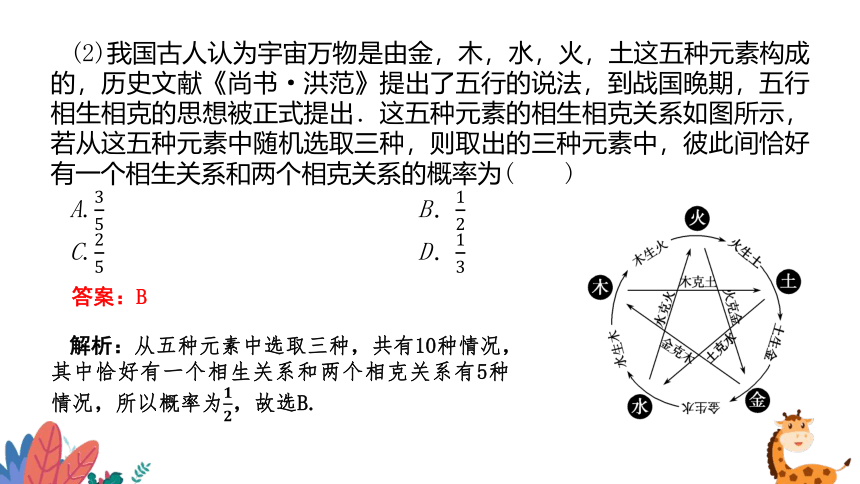
(2)我国古人认为宇宙万物是由金,木,水,火,土这五种元素构成的,历史文献《尚书·洪范》提出了五行的说法,到战国晚期,五行相生相克的思想被正式提出.这五种元素的相生相克关系如图所示,若从这五种元素中随机选取三种,则取出的三种元素中,彼此间恰好有一个相生关系和两个相克关系的概率为( )
A. B.
C. D.
答案:B
解析:从五种元素中选取三种,共有10种情况,其中恰好有一个相生关系和两个相克关系有5种情况,所以概率为,故选B.
归纳总结
1.求古典概型概率的两个关键点
(1)会利用枚举法、列表法等,求样本空间所含的基本事件数n以及事件A所含的基本事件数m;
(2)会运用古典概型的概率计算公式P(A)=求事件A发生的概率.
2.互斥事件、对立事件概率的求法
解决此类问题,首先应根据互斥事件和对立事件的定义分析出是不是互斥事件或对立事件,再选择概率公式进行计算.其方法有直接法和间接法.
对点训练
1.某校教师志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.今欲随机安排甲、乙2位志愿者为1位小学生辅导功课共4次,每位志愿者至少辅导1次,每次由1位志愿者辅导,则甲恰好辅导2次的概率为( )
A. B.
C. D.
答案:C
解析:由题意得所有不同方案有(甲,乙,乙,乙),(乙,甲,乙,乙),(乙,乙,甲,乙),(乙,乙,乙,甲),(甲,甲,乙,乙),(乙,乙,甲,甲),(甲,乙,乙,甲),(乙,甲,甲,乙),(甲,乙,甲,乙),(乙,甲,乙,甲),(乙,甲,甲,甲),(甲,乙,甲,甲),(甲,甲,乙,甲),(甲,甲,甲,乙),一共14个基本事件,其中(甲,甲,乙,乙),(乙,乙,甲,甲),(甲,乙,乙,甲),(乙,甲,甲,乙),(甲,乙,甲,乙),(乙,甲,乙,甲)共6个基本事件符合题意,故所求的概率为=,故选C.
2.已知a∈{-2,0,1,2,3},b∈{3,5},则函数f(x)=(a2-2)·ex+b为减函数的概率是( )
A. B.
C. D.
解析:函数f(x)=(a2-2)ex+b为减函数,则a2-2<0,-答案:C
3.如果一个三位数的十位上的数字比个位和百位上的数字都大,则称这个三位数为“凸数”(如132),现从集合{1,2,3,4}中任取3个互不相同的数字,组成一个三位数,则这个三位数是“凸数”的概率为( )
A. B.
C. D.
答案:B
解析:在集合{1,2,3,4}中任取3个不同的数组成一个三位数,不同的结果为:
(1)选取1,2,3,则不同的三位数有123,132,213,231,312,321;
(2)选取1,2,4,则不同的三位数有124,142,214,241,412,421;
(3)选取1,3,4,则不同的三位数有134,143,314,341,413,431;
(4)选取2,3,4,则不同的三位数有234,243,324,342,423,432.
综上,不同的三位数共有24个.
记“这个三位数是‘凸数’”为事件A,若一个三位数为“凸数”,则该三位数的十位上的数字比个位和百位上的数字都大,则十位上的数字只能为4或3.
当十位上的数字为4时,不同的“凸数”有142,143,241,243,341,342;
当十位上的数字为3时,不同的“凸数”有132,231.
综上,不同的“凸数”共有8个.故P(A)==. 故选B.
考点二 几何概型——定型定类,求量求值
1.几何概型的概率公式
P(A)=.
2.几何概型应满足两个条件
(1)试验中所有可能出现的结果(基本事件)有无限多个.
(2)每个基本事件出现的可能性相等.
[例2] (1)在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于的概率为( )
A. B.
C. D.
答案:B
解析:在区间(0,1)中随机取一个数,记为x,在区间(1,2)中随机取一个数,记为y,两数之和大于,即x+y>,则.在如图所示的平面直角坐标系中,点(x,y)构成的区域是边长为1的正方形区域(不含边界),事件A“两数之和大于”即
x+y>中,点(x,y)构成的区域为图中阴影部
分(不含边界),由几何概型的概率计算公式得
P(A)==,故选B.
(2) 如图所示的风车图案中,黑色部分和白色部分分别由全等的等腰直角三角形构成,在图案内随机取一点,则此点取自黑色部分的概率是( )
A. B. C. D.
答案:B
解析:设一个黑色等腰直角三角形的一条直角边长为a,则一个大白色等腰直角三角形的一条直角边长为a,黑色等腰直角三角形的面积为4×a2=2a2,大白色等腰直角三角形的面积为4××2a2=4a2,在图案内随机取一点,则此点取自黑色部分的概率是=,选B.
归纳总结
公式法求解几何概型的关键
(1)定型,即判断事件的属性——等可能性与无限性,确定所求概率模型为几何概型.
(2)定类,即确定所求事件的几何属性及其度量方式,确定其度量的类别——长度、角度、面积或体积等.
(3)求量,根据平面几何、立体几何的相关知识求出基本事件空间Ω度量及事件A的几何度量.
(4)求值,把所求的两个几何度量值代入几何概型的计算公式求值.
对点训练
1.阳马是底面为长方形,有一条侧棱与底面垂直的四棱锥.在阳马P-ABCD中,PC为阳马P-ABCD中最长的棱,AB=1,AD=2,PC=3,若在阳马P-ABCD的外接球内部随机取一点,则该点位于阳马内的概率为( )
A. B.
C. D.
答案:C
解析:根据题意,可知PC即为阳马P-ABCD的外接球的直径,
故外接球的体积V球=π×=.
由题意知,PA⊥平面ABCD,
则PC=,
所以3=,所以PA=2,则阳马P ABCD的体积V阳马P -ABCD=×1×2×2=.
所以所求概率P==.故选C.
2. 七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块小正方形和一块平行四边形共七块板组成的,如图是一个用七巧板拼成的大正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为________.
解析:设大正方形的边长为2,则该正方形的面积为4,阴影部分的面积为×1×2+1×=,所以在大正方形中任取一点,此点取自阴影部分的概率为=.
答案:
考点三 概率与统计的综合应用——准确审题,数据分析
角度1 概率与统计图表的交汇问题
[例3] 为了讴歌中华民族实现伟大复兴的奋斗历程,增进学生对党史的了解,某班级开展党史知识竞赛活动,现把50名学生的成绩绘制了如图所示的频率分布直方图.
(1)求a的值并估计这50名学生的平均成绩(同
一组中的数据用该组区间的中点值为代表);
(2)用分层抽样的方法从成绩在[80,90),[90,
100]两组学生中抽取5人进行培训,再从这5人
中随机抽取2人参加校级党史知识竞赛,求这
2人来自不同小组的概率.
解析:(1)根据频率分布直方图得:(0.004+0.006+a+0.030+0.024+0.016)×10=1,
解得a=0.020
估计平均成绩为:45×(0.004×10)+55×(0.006×10)+65×(0.020×10)+75×(0.030×10)+85×(0.024×10)+95×(0.016×10)=76.2.
(2)来自[80,90)小组的有3人记为a1,a2,a3,来自[90,100]小组的有2人记为b1,b2,从5人中随机抽取2人,基本事件为:a1a2,a1a3,a1b1,a1b2,a2a3,a2b1,a2b2,a3b1,a3b2,b1b2.
来自不同组的有a1b1,a1b2,a2b1,a2b2,a3b1,a3b2,
所以概率为P==.
角度2 概率统计与统计案例的交汇
[例4] 某汽车公司生产新能源汽车,2021年3~9月份销售量(单位:万辆)数据如下表所示:
月份x 3 4 5 6 7 8 9
销售量y/万辆 3.008 2.401 2.189 2.656 1.665 1.672 1.368
(1)某企业响应国家号召,购买了6辆该公司生产的新能源汽车,其中4月份生产的4辆,5月份生产的2辆,6辆汽车随机地分配给A,B两个部门使用,其中A部门用车4辆,B部门用车2辆.现了解该汽车公司2021年4月份生产的所有新能源汽车均存在安全隐患,需要召回.求该企业B部门2辆车中至多有1辆车被召回的概率.
(2)经分析可知,上述数据近似分布在一条直线附近.设y关于x的线性回归方程为=x+,根据表中数据可计算出=-0.246 5,试求出的值,并估计该公司10月份的销售量.
解析:(1)设该企业购买的6辆新能源汽车,4月份生产的4辆车分别为C1,C2,C3,C4,5月份生产的2辆车分别为D1,D2,6辆汽车随机地分配给A,B两个部门,B部门2辆车可能为(C1,C2),(C1,C3),(C1,C4),(C1,D1),(C1,D2),(C2,C3),(C2,C4),(C2,D1),(C2,D2),(C3,C4),(C3,D1),(C3,D2),(C4,D1),(C4,D2),(D1,D2),共15种情况.
其中,至多有1辆车是4月份生产的情况有(C1,D1),(C1,D2),(C2,D1),(C2,D2),(C3,D1),(C3,D2),(C4,D1),(C4,D2),(D1,D2),共9种,所以该企业B部门2辆车中至多有1辆车被召回的概率为P==.
(2)由题意得=6,=2.137.
因为回归直线过样本中心点(),所以2.137=6×(-0.246 5)+,解得=3.616.
当x=10时,=-0.246 5×10+3.616=1.151,
即该公司10月份销售量估计为1.151万辆.
角度3 概率、统计与函数的交汇
[例5] 某商店销售某海鲜,统计了春节前后50天海鲜的需求量x(10≤x≤20,单位:千克),得到频率分布直方图如图所示,已知该商店每天进货该海鲜1次,商店每销售1千克可获利50元.若供大于求,剩余的低价处理,每处理1千克亏损10元;若供不应求,可从其他商店调拨,销售1千克可获利30元.假设该商店在此期间每天进货该海鲜14千克,商店的日利润为y元.
(1)求商店的日利润y关于需求量x的函数表达式.
(2)假设同组中的每个数据用该组区间的中点值代替,视频率为概率.
①求这50天该商店销售该海鲜的日利润的平均数;
②估计日利润在区间[580,760)内的概率.
解析:(1)商店的日利润y关于需求量x的函数表达式为y=
化简得y=.
(2)①由频率分布直方图得:
海鲜需求量在区间[10,12)内的频率是2×0.08=0.16;
海鲜需求量在区间[12,14)内的频率是2×0.12=0.24;
海鲜需求量在区间[14,16)内的频率是2×0.15=0.30;
海鲜需求量在区间[16,18)内的频率是2×0.10=0.20;
海鲜需求量在区间[18,20]内的频率是2×0.05=0.10.
所以这50天商店销售该海鲜的日利润y的平均数为:
(11×60-140)×0.16+(13×60-140)×0.24+(15×30+280)×0.30+(17×30+280)×0.20+(19×30+280)×0.10=83.2+153.6+219+158+85=698.8(元).
②易知y=在区间[10,20]上单调递增,
当y=580时,可得x=12,当y=760时,可得x=16.
所以日利润y在区间[580,760)内的概率即为海鲜需求量x在区间[12,16)内的频率,即0.24+0.30=0.54.
归纳总结
对于统计与函数结合的问题,一般而言,自变量取值发生变化,对应的关系也将发生变化,故所得函数大多是分段函数.研究统计问题中由于自变量变化带来的影响时,要注意不同范围内对应的不同关系,并遵循解决含分段函数的问题的基本原则:分段函数,分段研究.
对点训练
1.某篮球队在本赛季已结束的8场比赛中,队员甲得分统计的茎叶图如图所示.
(1)求甲在比赛中得分的均值和方差的大小;
(2)从甲比赛得分在20分以下的6场比赛中随机抽取2场进行失误分析,求抽取2场都不超过均值的概率.
解析:(1)甲在比赛中得分的均值=×(7+8+10+15+17+19+21+23)=15,方差s2=×[(-8)2+(-7)2+(-5)2+02+22+42+62+82]=32.25.
(2)甲比赛得分在20分以下的分数为:7,8,10,15,17,19.
从中随机抽取2场,这2场比赛的得分如下:
(7,8),(7,10),(7,15),(7,17),(7,19),(8,10),(8,15),(8,17),(8,19),(10,15),(10,17),(10,19),(15,17),(15,19),(17,19).共15种.
其中抽到2场都不超过均值的情形是:
(7,8),(7,10),(7,15),(8,10),(8,15),(10,15),共6种,
所以所求概率P==.
2.英国时间2020年1月31日23时,英国顺利脱欧.在此之前,英国脱欧这件国际大事被社会各界广泛关注,2019英国大选之后,人们预计英国将会在2020年1月31日完成脱欧,但是因为之前脱欧多次被延期,所以很多人认为并不能如期完成.某媒体随机在人群中抽取了100人进行调查,其中40岁及以上的55人中有10人认为不能如期完成,40岁以下的人中认为能如期完成的占.
(1)完成2×2列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
(2)从上述100人中,按年龄采用分层抽样的方法抽取20人,再从这20人中选取40岁以下的2人进行深度调查,则2人中恰有1人认为英国能如期完成脱欧的概率为多少?
能如期完成 不能如期完成 总计
40岁及以上
40岁以下
总计
解析:(1)由题意可得补充完整的列联表如表:
所以K2==≈3.030,
由附表知:P(K2>2.706)=0.100,且3.030>2.706,所以有90%的把握认为“预测国际大事的准确率与年龄有关”.
能如期完成 不能如期完成 总计
40岁及以上 45 10 55
40岁以下 30 15 45
总计 75 25 100
(2)40岁及以上的人数为55,40岁以下的人数为45,比例为11∶9,抽取的20人中,40岁以下的有9人,其中有6人认为能如期完成,分别记为a,b,c,d,e,f,有3人认为不能如期完成,分别记为A,B,C,从这9人中抽取2人,有(a,b),(a,c),(a,d),(a,e),(a,f),(a,A),(a,B),(a,C),(b,c),(b,d),(b,e),(b,f),(b,A),(b,B),(b,C),(c,d),(c,e),(c,f),(c,A),(c,B),(c,C),(d,e),(d,f),(d,A),(d,B),(d,C),(e,f),(e,A),(e,B),(e,C),(f,A),(f,B),(f,C),(A,B),(A,C),(B,C),共36个基本事件.
设事件M:从20人中抽取的40岁以下的2人中恰有1人认为能如期完成脱欧.则事件M包括(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(c,A),(c,B),(c,C),(d,A),(d,B),(d,C),(e,A),(e,B),(e,C),(f,A),(f,B),(f,C),共18个基本事件,所以P(M)==,
所以从20人中选取40岁以下的2人进行深度调查,2人中恰有1人认为英国能如期完成脱欧的概率为.
概率与统计问题辨析、辨型与辨图的基本策略
(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立等.
(2)理清事件以什么形式发生,如同时发生、至少有几个发生等.
(3)明确抽取方式,如放回还是不放回、抽取有无顺序等.
(4)分清是古典概型还是几何概型后再求概率.
(5)会套用求、K2的公式,再作进一步求值与分析.
(6)理解各图表所给信息,利用信息找出所要数据.
[典例] 某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用水量 [0, 0.1) [0.1, 0.2) [0.2, 0.3) [0.3, 0.4) [0.4, 0.5) [0.5, 0.6) [0.6,
0.7]
频数 1 3 2 4 9 26 5
使用了节水龙头50天的日用水量频数分布表
日用水量 [0, 0.1) [0.1, 0.2) [0.2, 0.3) [0.3, 0.4) [0.4, 0.5) [0.5,
0.6]
频数 1 5 13 10 16 5
(1)在右图中作出使用了节水龙头50天的日用水量数据的频率分布直方图;
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表)
(1)频率分布直方图如图所示.
(2)根据频率分布直方图知,
该家庭使用节水龙头后50天日
用水量小于0.35 m3的频率为
0.2×0.1+1×0.1+2.6×0.1+
2×0.05=0.48,
因此该家庭使用节水龙头后,日用水量小于0.35 m3的概率的估计值为0.48.
(3)该家庭未使用节水龙头50天日用水量的平均数为
=×(0.05×1+0.15×3+0.25×2+0.35×4+0.45×9+0.55×26+0.65×5)=0.48.
该家庭使用了节水龙头后50天日用水量的平均数为
=×(0.05×1+0.15×5+0.25×13+0.35×10+0.45×16+0.55×5)=0.35.
估计使用节水龙头后,一年可节省水(0.48-0.35)×365=47.45(m3).
(1)求概率的关键:定型——定性——定数量(几何量)——求概率.
(2)求解统计案例问题的关键:作图(列表格)——计算——得结论.
冲刺高考(文科数学) 概率
考点一 古典概型——巧选方法,熟用公式
1.古典概型的概率公式
P(A)==.
2.古典概型的两个特点
(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件出现的可能性相等.
[例1] (1)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A. B.
C. D.
解析:从O,A,B,C,D中任取3点的情况有(O,A,B),(O,A,C),(O,A,D),(O,B,C),(O,B,D),(O,C,D),(A,B,C),(A,B,D),(B,C,D),(A,C,D),共有10种不同的情况,由图可知取到的3点共线的有(O,A,C)和(O,B,D)两种情况,所以所求概率为=.故选A.
答案:A
(2)我国古人认为宇宙万物是由金,木,水,火,土这五种元素构成的,历史文献《尚书·洪范》提出了五行的说法,到战国晚期,五行相生相克的思想被正式提出.这五种元素的相生相克关系如图所示,若从这五种元素中随机选取三种,则取出的三种元素中,彼此间恰好有一个相生关系和两个相克关系的概率为( )
A. B.
C. D.
答案:B
解析:从五种元素中选取三种,共有10种情况,其中恰好有一个相生关系和两个相克关系有5种情况,所以概率为,故选B.
归纳总结
1.求古典概型概率的两个关键点
(1)会利用枚举法、列表法等,求样本空间所含的基本事件数n以及事件A所含的基本事件数m;
(2)会运用古典概型的概率计算公式P(A)=求事件A发生的概率.
2.互斥事件、对立事件概率的求法
解决此类问题,首先应根据互斥事件和对立事件的定义分析出是不是互斥事件或对立事件,再选择概率公式进行计算.其方法有直接法和间接法.
对点训练
1.某校教师志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.今欲随机安排甲、乙2位志愿者为1位小学生辅导功课共4次,每位志愿者至少辅导1次,每次由1位志愿者辅导,则甲恰好辅导2次的概率为( )
A. B.
C. D.
答案:C
解析:由题意得所有不同方案有(甲,乙,乙,乙),(乙,甲,乙,乙),(乙,乙,甲,乙),(乙,乙,乙,甲),(甲,甲,乙,乙),(乙,乙,甲,甲),(甲,乙,乙,甲),(乙,甲,甲,乙),(甲,乙,甲,乙),(乙,甲,乙,甲),(乙,甲,甲,甲),(甲,乙,甲,甲),(甲,甲,乙,甲),(甲,甲,甲,乙),一共14个基本事件,其中(甲,甲,乙,乙),(乙,乙,甲,甲),(甲,乙,乙,甲),(乙,甲,甲,乙),(甲,乙,甲,乙),(乙,甲,乙,甲)共6个基本事件符合题意,故所求的概率为=,故选C.
2.已知a∈{-2,0,1,2,3},b∈{3,5},则函数f(x)=(a2-2)·ex+b为减函数的概率是( )
A. B.
C. D.
解析:函数f(x)=(a2-2)ex+b为减函数,则a2-2<0,-
3.如果一个三位数的十位上的数字比个位和百位上的数字都大,则称这个三位数为“凸数”(如132),现从集合{1,2,3,4}中任取3个互不相同的数字,组成一个三位数,则这个三位数是“凸数”的概率为( )
A. B.
C. D.
答案:B
解析:在集合{1,2,3,4}中任取3个不同的数组成一个三位数,不同的结果为:
(1)选取1,2,3,则不同的三位数有123,132,213,231,312,321;
(2)选取1,2,4,则不同的三位数有124,142,214,241,412,421;
(3)选取1,3,4,则不同的三位数有134,143,314,341,413,431;
(4)选取2,3,4,则不同的三位数有234,243,324,342,423,432.
综上,不同的三位数共有24个.
记“这个三位数是‘凸数’”为事件A,若一个三位数为“凸数”,则该三位数的十位上的数字比个位和百位上的数字都大,则十位上的数字只能为4或3.
当十位上的数字为4时,不同的“凸数”有142,143,241,243,341,342;
当十位上的数字为3时,不同的“凸数”有132,231.
综上,不同的“凸数”共有8个.故P(A)==. 故选B.
考点二 几何概型——定型定类,求量求值
1.几何概型的概率公式
P(A)=.
2.几何概型应满足两个条件
(1)试验中所有可能出现的结果(基本事件)有无限多个.
(2)每个基本事件出现的可能性相等.
[例2] (1)在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于的概率为( )
A. B.
C. D.
答案:B
解析:在区间(0,1)中随机取一个数,记为x,在区间(1,2)中随机取一个数,记为y,两数之和大于,即x+y>,则.在如图所示的平面直角坐标系中,点(x,y)构成的区域是边长为1的正方形区域(不含边界),事件A“两数之和大于”即
x+y>中,点(x,y)构成的区域为图中阴影部
分(不含边界),由几何概型的概率计算公式得
P(A)==,故选B.
(2) 如图所示的风车图案中,黑色部分和白色部分分别由全等的等腰直角三角形构成,在图案内随机取一点,则此点取自黑色部分的概率是( )
A. B. C. D.
答案:B
解析:设一个黑色等腰直角三角形的一条直角边长为a,则一个大白色等腰直角三角形的一条直角边长为a,黑色等腰直角三角形的面积为4×a2=2a2,大白色等腰直角三角形的面积为4××2a2=4a2,在图案内随机取一点,则此点取自黑色部分的概率是=,选B.
归纳总结
公式法求解几何概型的关键
(1)定型,即判断事件的属性——等可能性与无限性,确定所求概率模型为几何概型.
(2)定类,即确定所求事件的几何属性及其度量方式,确定其度量的类别——长度、角度、面积或体积等.
(3)求量,根据平面几何、立体几何的相关知识求出基本事件空间Ω度量及事件A的几何度量.
(4)求值,把所求的两个几何度量值代入几何概型的计算公式求值.
对点训练
1.阳马是底面为长方形,有一条侧棱与底面垂直的四棱锥.在阳马P-ABCD中,PC为阳马P-ABCD中最长的棱,AB=1,AD=2,PC=3,若在阳马P-ABCD的外接球内部随机取一点,则该点位于阳马内的概率为( )
A. B.
C. D.
答案:C
解析:根据题意,可知PC即为阳马P-ABCD的外接球的直径,
故外接球的体积V球=π×=.
由题意知,PA⊥平面ABCD,
则PC=,
所以3=,所以PA=2,则阳马P ABCD的体积V阳马P -ABCD=×1×2×2=.
所以所求概率P==.故选C.
2. 七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块小正方形和一块平行四边形共七块板组成的,如图是一个用七巧板拼成的大正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为________.
解析:设大正方形的边长为2,则该正方形的面积为4,阴影部分的面积为×1×2+1×=,所以在大正方形中任取一点,此点取自阴影部分的概率为=.
答案:
考点三 概率与统计的综合应用——准确审题,数据分析
角度1 概率与统计图表的交汇问题
[例3] 为了讴歌中华民族实现伟大复兴的奋斗历程,增进学生对党史的了解,某班级开展党史知识竞赛活动,现把50名学生的成绩绘制了如图所示的频率分布直方图.
(1)求a的值并估计这50名学生的平均成绩(同
一组中的数据用该组区间的中点值为代表);
(2)用分层抽样的方法从成绩在[80,90),[90,
100]两组学生中抽取5人进行培训,再从这5人
中随机抽取2人参加校级党史知识竞赛,求这
2人来自不同小组的概率.
解析:(1)根据频率分布直方图得:(0.004+0.006+a+0.030+0.024+0.016)×10=1,
解得a=0.020
估计平均成绩为:45×(0.004×10)+55×(0.006×10)+65×(0.020×10)+75×(0.030×10)+85×(0.024×10)+95×(0.016×10)=76.2.
(2)来自[80,90)小组的有3人记为a1,a2,a3,来自[90,100]小组的有2人记为b1,b2,从5人中随机抽取2人,基本事件为:a1a2,a1a3,a1b1,a1b2,a2a3,a2b1,a2b2,a3b1,a3b2,b1b2.
来自不同组的有a1b1,a1b2,a2b1,a2b2,a3b1,a3b2,
所以概率为P==.
角度2 概率统计与统计案例的交汇
[例4] 某汽车公司生产新能源汽车,2021年3~9月份销售量(单位:万辆)数据如下表所示:
月份x 3 4 5 6 7 8 9
销售量y/万辆 3.008 2.401 2.189 2.656 1.665 1.672 1.368
(1)某企业响应国家号召,购买了6辆该公司生产的新能源汽车,其中4月份生产的4辆,5月份生产的2辆,6辆汽车随机地分配给A,B两个部门使用,其中A部门用车4辆,B部门用车2辆.现了解该汽车公司2021年4月份生产的所有新能源汽车均存在安全隐患,需要召回.求该企业B部门2辆车中至多有1辆车被召回的概率.
(2)经分析可知,上述数据近似分布在一条直线附近.设y关于x的线性回归方程为=x+,根据表中数据可计算出=-0.246 5,试求出的值,并估计该公司10月份的销售量.
解析:(1)设该企业购买的6辆新能源汽车,4月份生产的4辆车分别为C1,C2,C3,C4,5月份生产的2辆车分别为D1,D2,6辆汽车随机地分配给A,B两个部门,B部门2辆车可能为(C1,C2),(C1,C3),(C1,C4),(C1,D1),(C1,D2),(C2,C3),(C2,C4),(C2,D1),(C2,D2),(C3,C4),(C3,D1),(C3,D2),(C4,D1),(C4,D2),(D1,D2),共15种情况.
其中,至多有1辆车是4月份生产的情况有(C1,D1),(C1,D2),(C2,D1),(C2,D2),(C3,D1),(C3,D2),(C4,D1),(C4,D2),(D1,D2),共9种,所以该企业B部门2辆车中至多有1辆车被召回的概率为P==.
(2)由题意得=6,=2.137.
因为回归直线过样本中心点(),所以2.137=6×(-0.246 5)+,解得=3.616.
当x=10时,=-0.246 5×10+3.616=1.151,
即该公司10月份销售量估计为1.151万辆.
角度3 概率、统计与函数的交汇
[例5] 某商店销售某海鲜,统计了春节前后50天海鲜的需求量x(10≤x≤20,单位:千克),得到频率分布直方图如图所示,已知该商店每天进货该海鲜1次,商店每销售1千克可获利50元.若供大于求,剩余的低价处理,每处理1千克亏损10元;若供不应求,可从其他商店调拨,销售1千克可获利30元.假设该商店在此期间每天进货该海鲜14千克,商店的日利润为y元.
(1)求商店的日利润y关于需求量x的函数表达式.
(2)假设同组中的每个数据用该组区间的中点值代替,视频率为概率.
①求这50天该商店销售该海鲜的日利润的平均数;
②估计日利润在区间[580,760)内的概率.
解析:(1)商店的日利润y关于需求量x的函数表达式为y=
化简得y=.
(2)①由频率分布直方图得:
海鲜需求量在区间[10,12)内的频率是2×0.08=0.16;
海鲜需求量在区间[12,14)内的频率是2×0.12=0.24;
海鲜需求量在区间[14,16)内的频率是2×0.15=0.30;
海鲜需求量在区间[16,18)内的频率是2×0.10=0.20;
海鲜需求量在区间[18,20]内的频率是2×0.05=0.10.
所以这50天商店销售该海鲜的日利润y的平均数为:
(11×60-140)×0.16+(13×60-140)×0.24+(15×30+280)×0.30+(17×30+280)×0.20+(19×30+280)×0.10=83.2+153.6+219+158+85=698.8(元).
②易知y=在区间[10,20]上单调递增,
当y=580时,可得x=12,当y=760时,可得x=16.
所以日利润y在区间[580,760)内的概率即为海鲜需求量x在区间[12,16)内的频率,即0.24+0.30=0.54.
归纳总结
对于统计与函数结合的问题,一般而言,自变量取值发生变化,对应的关系也将发生变化,故所得函数大多是分段函数.研究统计问题中由于自变量变化带来的影响时,要注意不同范围内对应的不同关系,并遵循解决含分段函数的问题的基本原则:分段函数,分段研究.
对点训练
1.某篮球队在本赛季已结束的8场比赛中,队员甲得分统计的茎叶图如图所示.
(1)求甲在比赛中得分的均值和方差的大小;
(2)从甲比赛得分在20分以下的6场比赛中随机抽取2场进行失误分析,求抽取2场都不超过均值的概率.
解析:(1)甲在比赛中得分的均值=×(7+8+10+15+17+19+21+23)=15,方差s2=×[(-8)2+(-7)2+(-5)2+02+22+42+62+82]=32.25.
(2)甲比赛得分在20分以下的分数为:7,8,10,15,17,19.
从中随机抽取2场,这2场比赛的得分如下:
(7,8),(7,10),(7,15),(7,17),(7,19),(8,10),(8,15),(8,17),(8,19),(10,15),(10,17),(10,19),(15,17),(15,19),(17,19).共15种.
其中抽到2场都不超过均值的情形是:
(7,8),(7,10),(7,15),(8,10),(8,15),(10,15),共6种,
所以所求概率P==.
2.英国时间2020年1月31日23时,英国顺利脱欧.在此之前,英国脱欧这件国际大事被社会各界广泛关注,2019英国大选之后,人们预计英国将会在2020年1月31日完成脱欧,但是因为之前脱欧多次被延期,所以很多人认为并不能如期完成.某媒体随机在人群中抽取了100人进行调查,其中40岁及以上的55人中有10人认为不能如期完成,40岁以下的人中认为能如期完成的占.
(1)完成2×2列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
(2)从上述100人中,按年龄采用分层抽样的方法抽取20人,再从这20人中选取40岁以下的2人进行深度调查,则2人中恰有1人认为英国能如期完成脱欧的概率为多少?
能如期完成 不能如期完成 总计
40岁及以上
40岁以下
总计
解析:(1)由题意可得补充完整的列联表如表:
所以K2==≈3.030,
由附表知:P(K2>2.706)=0.100,且3.030>2.706,所以有90%的把握认为“预测国际大事的准确率与年龄有关”.
能如期完成 不能如期完成 总计
40岁及以上 45 10 55
40岁以下 30 15 45
总计 75 25 100
(2)40岁及以上的人数为55,40岁以下的人数为45,比例为11∶9,抽取的20人中,40岁以下的有9人,其中有6人认为能如期完成,分别记为a,b,c,d,e,f,有3人认为不能如期完成,分别记为A,B,C,从这9人中抽取2人,有(a,b),(a,c),(a,d),(a,e),(a,f),(a,A),(a,B),(a,C),(b,c),(b,d),(b,e),(b,f),(b,A),(b,B),(b,C),(c,d),(c,e),(c,f),(c,A),(c,B),(c,C),(d,e),(d,f),(d,A),(d,B),(d,C),(e,f),(e,A),(e,B),(e,C),(f,A),(f,B),(f,C),(A,B),(A,C),(B,C),共36个基本事件.
设事件M:从20人中抽取的40岁以下的2人中恰有1人认为能如期完成脱欧.则事件M包括(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(c,A),(c,B),(c,C),(d,A),(d,B),(d,C),(e,A),(e,B),(e,C),(f,A),(f,B),(f,C),共18个基本事件,所以P(M)==,
所以从20人中选取40岁以下的2人进行深度调查,2人中恰有1人认为英国能如期完成脱欧的概率为.
概率与统计问题辨析、辨型与辨图的基本策略
(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立等.
(2)理清事件以什么形式发生,如同时发生、至少有几个发生等.
(3)明确抽取方式,如放回还是不放回、抽取有无顺序等.
(4)分清是古典概型还是几何概型后再求概率.
(5)会套用求、K2的公式,再作进一步求值与分析.
(6)理解各图表所给信息,利用信息找出所要数据.
[典例] 某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用水量 [0, 0.1) [0.1, 0.2) [0.2, 0.3) [0.3, 0.4) [0.4, 0.5) [0.5, 0.6) [0.6,
0.7]
频数 1 3 2 4 9 26 5
使用了节水龙头50天的日用水量频数分布表
日用水量 [0, 0.1) [0.1, 0.2) [0.2, 0.3) [0.3, 0.4) [0.4, 0.5) [0.5,
0.6]
频数 1 5 13 10 16 5
(1)在右图中作出使用了节水龙头50天的日用水量数据的频率分布直方图;
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表)
(1)频率分布直方图如图所示.
(2)根据频率分布直方图知,
该家庭使用节水龙头后50天日
用水量小于0.35 m3的频率为
0.2×0.1+1×0.1+2.6×0.1+
2×0.05=0.48,
因此该家庭使用节水龙头后,日用水量小于0.35 m3的概率的估计值为0.48.
(3)该家庭未使用节水龙头50天日用水量的平均数为
=×(0.05×1+0.15×3+0.25×2+0.35×4+0.45×9+0.55×26+0.65×5)=0.48.
该家庭使用了节水龙头后50天日用水量的平均数为
=×(0.05×1+0.15×5+0.25×13+0.35×10+0.45×16+0.55×5)=0.35.
估计使用节水龙头后,一年可节省水(0.48-0.35)×365=47.45(m3).
(1)求概率的关键:定型——定性——定数量(几何量)——求概率.
(2)求解统计案例问题的关键:作图(列表格)——计算——得结论.
同课章节目录
