2021—2022学年度人教版七年级数学下册5.3 平行线的性质 课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年度人教版七年级数学下册5.3 平行线的性质 课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 487.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 10:33:24 | ||
图片预览


文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线 5.3平行线的性质 课后练习
一、选择题
1.下列选项中,可以作为命题“一个钝角与一个锐角的差是锐角”的反例是( )
A. B. C. D.
2.一副直角三角板叠放如图所示,现将含角的三角板固定不动,把含角的三角板绕直角顶点按每秒的速度沿逆时针方向匀速旋转一周,当两块三角板的斜边平行时,则三角板旋转运动的时间为( )
A.5秒或7秒 B.5秒或19秒 C.5秒或17秒 D.7秒或19秒
3.如图,,平分,,,,有下列结论:①;②平分;③;④.其中正确结论的个数为( )
A.个 B.个 C.个 D.个
4.如图,已知,平分,平分,则下列判断:①;②平分;③;④中,正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,直线,,则的度数为( )
A. B. C. D.
6.如图,直线,三角板的直角顶点在直线上,已知,则等于( ).
A.25° B.55° C.65° D.75°
7.如图,已知平分,平分,.下列结论正确的有( )
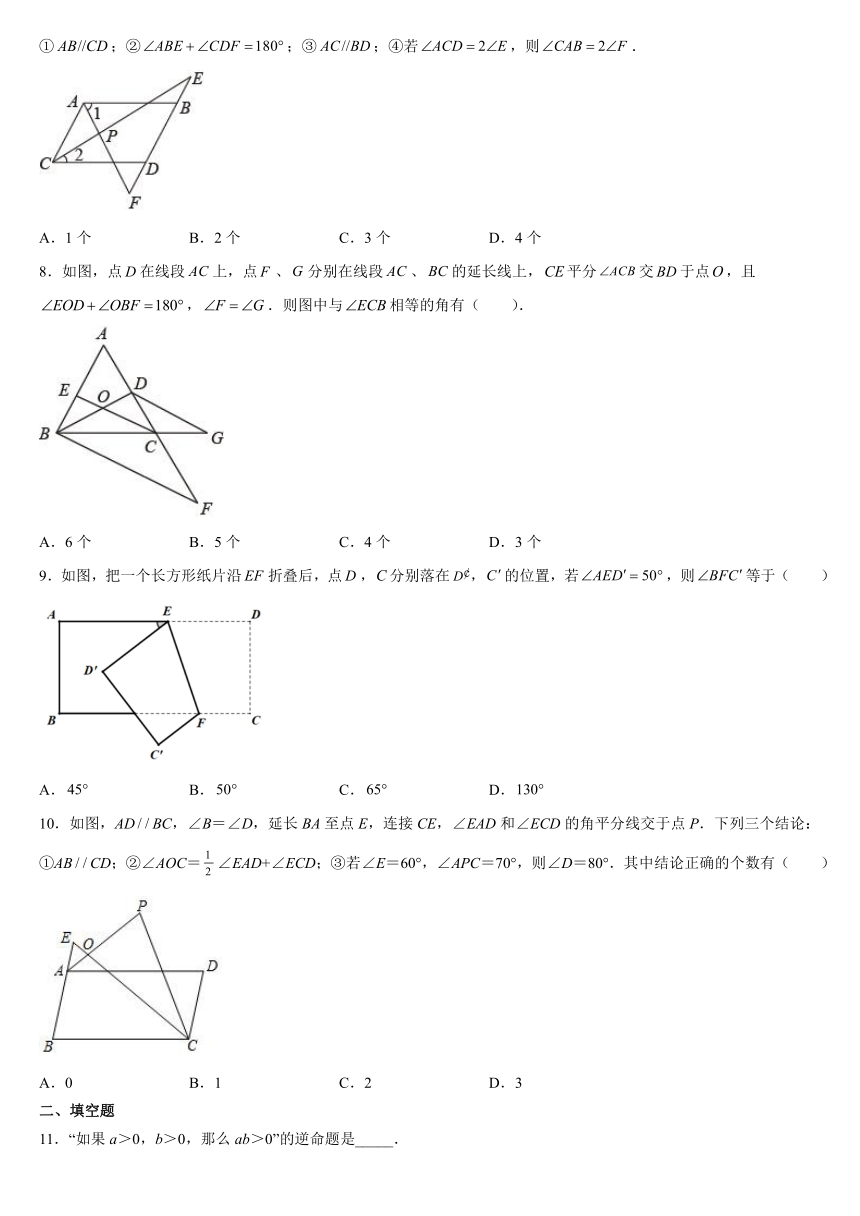
①;②;③;④若,则.
A.1个 B.2个 C.3个 D.4个
8.如图,点在线段上,点、分别在线段、的延长线上,平分交于点,且,.则图中与相等的角有( ).
A.6个 B.5个 C.4个 D.3个
9.如图,把一个长方形纸片沿折叠后,点,分别落在,的位置,若,则等于( )
A. B. C. D.
10.如图,ADBC,∠B=∠D,延长BA至点E,连接CE,∠EAD和∠ECD的角平分线交于点P.下列三个结论:
①ABCD;②∠AOC=∠EAD+∠ECD;③若∠E=60°,∠APC=70°,则∠D=80°.其中结论正确的个数有( )
A.0 B.1 C.2 D.3
二、填空题
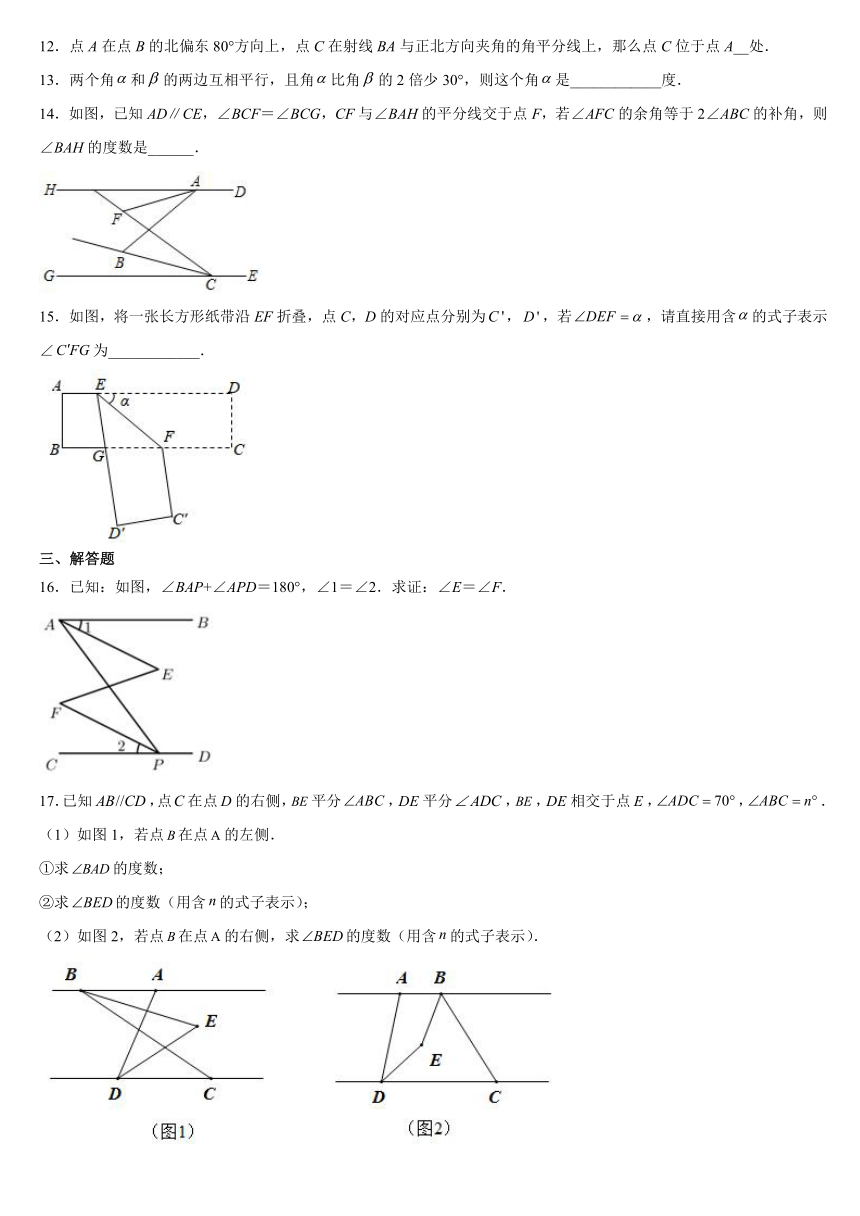
11.“如果a>0,b>0,那么ab>0”的逆命题是_____.
12.点A在点B的北偏东80°方向上,点C在射线BA与正北方向夹角的角平分线上,那么点C位于点A__处.
13.两个角和的两边互相平行,且角比角的2倍少30°,则这个角是____________度.
14.如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠ABC的补角,则∠BAH的度数是______.
15.如图,将一张长方形纸带沿EF折叠,点C,D的对应点分别为,,若,请直接用含的式子表示∠为____________.
三、解答题
16.已知:如图,∠BAP+∠APD=180°,∠1=∠2.求证:∠E=∠F.
17.已知,点在点的右侧,平分,平分,,相交于点,,.
(1)如图1,若点在点的左侧.
①求的度数;
②求的度数(用含的式子表示);
(2)如图2,若点在点的右侧,求的度数(用含的式子表示).
18.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,
①求∠BEC的度数;
②如图2,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
19.如图,已知:,垂足为点,,垂足为点,点在上,连接.
(1)与平行吗?为什么?
(2)若、,求的度数.
20.如图1,∠EFH=90°,点A、C分别在射线FE和FH上,AB∥CD.
(1)若∠FAB=150°,则∠HCD= °;
(2)小明同学发现:无论∠FAB如何变化,∠FAB﹣∠HCD的值始终为定值,并给出了一种证明该发现的辅助线作法:如图2,过A作AM∥FH,交CD于M,请你根据小明同学提供的辅助线(或自己添加其它辅助线),先确定该定值,并说明理由;
(3)如图3,把“∠EFH=90°”改为“∠EFH=120°”,其它条件保持不变,猜想∠FAB与∠HCD的数量关系,并说明理由.
21.如图,已知四边形ABCD中,∠A=106°﹣α,∠ABC=74°+α,BD⊥DC于D,EF⊥DC于F,求证:∠1=∠2.
22.如图,点A在直线PQ上,点C在直线MN上,PQ∥MN,∠CAQ=60°,CB平分∠ACM.(作答过程不需要写依据)
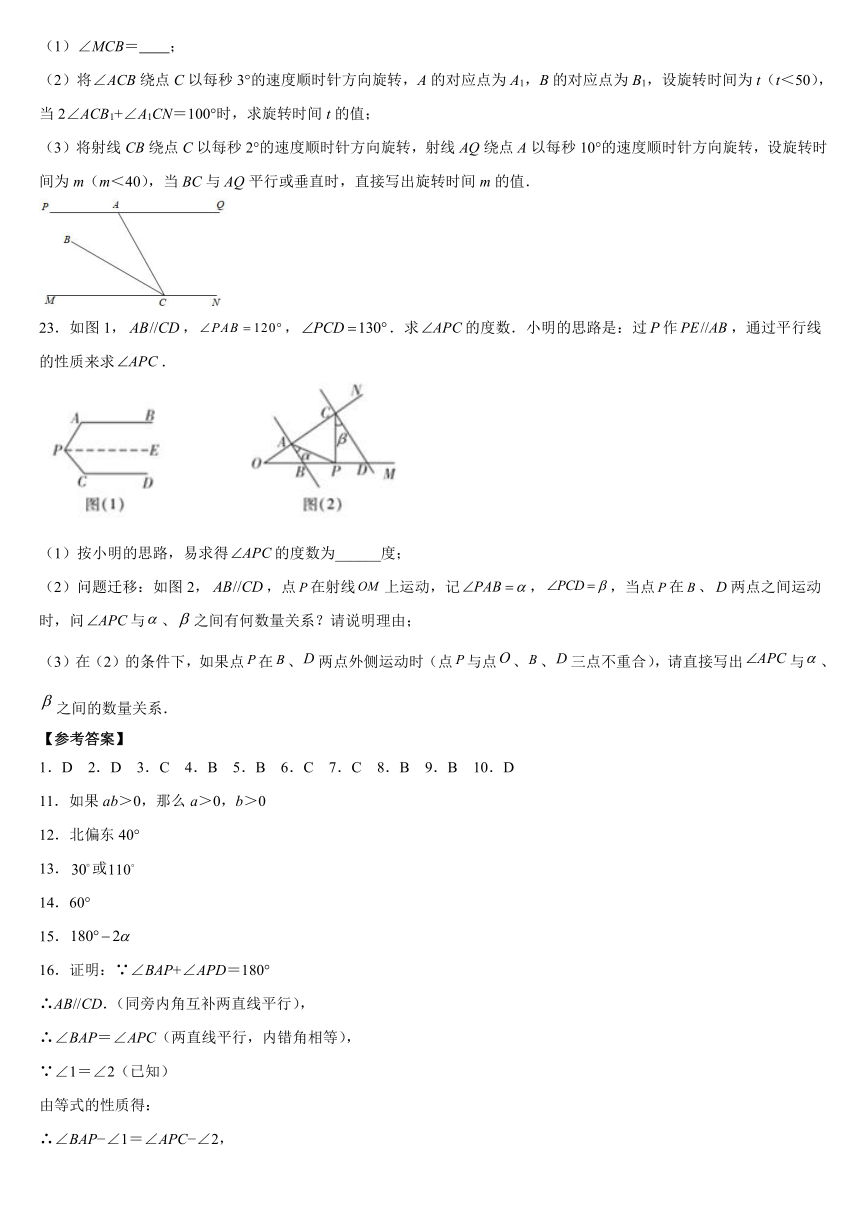
(1)∠MCB= ;
(2)将∠ACB绕点C以每秒3°的速度顺时针方向旋转,A的对应点为A1,B的对应点为B1,设旋转时间为t(t<50),当2∠ACB1+∠A1CN=100°时,求旋转时间t的值;
(3)将射线CB绕点C以每秒2°的速度顺时针方向旋转,射线AQ绕点A以每秒10°的速度顺时针方向旋转,设旋转时间为m(m<40),当BC与AQ平行或垂直时,直接写出旋转时间m的值.
23.如图1,,,.求的度数.小明的思路是:过作,通过平行线的性质来求.
(1)按小明的思路,易求得的度数为______度;
(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.
【参考答案】
1.D 2.D 3.C 4.B 5.B 6.C 7.C 8.B 9.B 10.D
11.如果ab>0,那么a>0,b>0
12.北偏东40°
13.或
14.60°
15.
16.证明:∵∠BAP+∠APD=180°
∴AB//CD.(同旁内角互补两直线平行),
∴∠BAP=∠APC(两直线平行,内错角相等),
∵∠1=∠2(已知)
由等式的性质得:
∴∠BAP ∠1=∠APC ∠2,
即∠EAP=∠FPA,
∴AE//FP(内错角相等,两直线平行),
∴∠E=∠F(由两直线平行,内错角相等),
17.(1)①AB//CD,∠ADC=70°,
∴∠BAD=70°;
②如图1,过点E作EF//AB,
∵AB//CD,
∴AAB//CD//EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=n°+35°;
(2)如图2,过点E作EF//AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB//CD,
∴AB//CD//EF,
∴∠BEF=180° ∠ABE=180° n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180° n°+35°=215° n°.
18.(1)证明:∵DE∥BC,
∴∠ADE=∠ABC,
∵∠BCF+∠ADE=180°,
∴∠BCF+∠ABC=180°,
∴CF∥AB;
(2)①解:如图,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
②∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG-∠EBC=40°-28°=12°.
19.(1)理由如下:
∵,
∴
∴(同位角相等,两直线平行)
(2)∵
∴(两直线平行,同位角相等)
∵
∴
∴(内错角相等,两直线平行)
∴(两直线平行,同位角相等)
20.解:(1)如图,过点F作FG∥AB,
∵FG∥AB,∠FAB=150°,
∴∠AFG+∠FAB=180°,
∴∠AFG=180°﹣∠FAB=180°﹣150°=30°,
∵∠EFH=90°,
∴∠CFG=∠EFH﹣∠AFG=90°﹣30°=60°,
∵AB∥CD,
∴FG∥CD,
∴∠HCD=∠CFG=60°,
故答案为:60°;
(2)∠FAB﹣∠HCD=90°,理由如下:
∵AM∥FH,∠EFH=90°,
∴∠EFH+∠FAM=180°,∠HCD=∠AMC,
∴∠FAM=180°﹣∠EFH=180°﹣90°=90°,
∵AB∥CD,
∴∠BAM=∠AMC,
∴∠HCD=∠BAM,
∴∠FAB﹣∠HCD=∠FAB﹣∠BAM=∠FAM=90°,
∴无论∠FAB如何变化,∠FAB﹣∠HCD的值始终为定值90°;
(3)∠FAB﹣∠HCD=60°,理由如下:
如图,过点A作AN∥FH交CD于点N,
∵AN∥FH,∠EFH=120°,
∴∠EFH+∠FAN=180°,∠HCD=∠ANC,
∴∠FAN=180°﹣∠EFH=180°﹣120°=60°,
∵AB∥CD,
∴∠BAN=∠ANC,
∴∠BAN=∠HCD,
∴∠FAB﹣∠HCD=∠FAB﹣∠BAN=∠FAN=60°.
21.证明:∵∠A=106°﹣α,∠ABC=74°+α,
∴∠A+∠ABC=180°,
∴AD∥BC,
∴∠1=∠DBC,
∵BD⊥DC,EF⊥DC,
∴∠BDC=∠EFC=90°,
∴BD∥EF,
∴∠2=∠DBC,
∴∠1=∠2.
22.解:(1)∵PQ∥MN,∠CAQ=60°,
∴∠ACM=∠CAQ=60°.
又∵CB平分∠ACM,
∴∠MCB=30°.
故答案为:30°.
(2)∵t<50,
∴可旋转的度数3×50=150°<180°,即B不会运动到直线CN上.
①当B1在A的左边时,t<30÷3=10,∠ACN=120°,
∴∠ACB1=30﹣3t,∠A1CN=120﹣3t
又∵2∠ACB1+∠A1CN=100°,
∴2(30﹣3t)+120﹣3t=100,
∴t=.
②当A1和B1在∠ACN之间时,10≤t≤40,
∴∠ACB1=3t﹣30,∠A1CN=120﹣3t.
又∵2∠ACB1+∠A1CN=100°,
∴2(3t﹣30)+120﹣3t=100,
∴t=.
③当B1在∠ACN之间,A1在直线CN下方时,40<t<50,
∴∠ACB1=3t﹣30,∠A1CN=3t﹣120.
又∵2∠ACB1+∠A1CN=100°,
∴2(3t﹣30)+3t﹣120=100,
∴t=(舍去).
∴综上所述,t的取值为或;
(3)∵m<40,
∴当BC∥AQ时有两种:30+2m=10m或30+2m=10m﹣180,
解得m=3.75,26.25.
∴当BC⊥AQ时有三种情况:30+2m+10m=90,30+2m+10m=270,30+2m+10m=450,
解得m=5,12,35.
答: m的值为3.75,26.25,5,20,35.
23.解:(1)∵AB∥CD,PE∥AB,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵,,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)
理由:过作交于,
∵,
∴
∴,,
∴;
(3)①当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
②当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
综上所述,
一、选择题
1.下列选项中,可以作为命题“一个钝角与一个锐角的差是锐角”的反例是( )
A. B. C. D.
2.一副直角三角板叠放如图所示,现将含角的三角板固定不动,把含角的三角板绕直角顶点按每秒的速度沿逆时针方向匀速旋转一周,当两块三角板的斜边平行时,则三角板旋转运动的时间为( )
A.5秒或7秒 B.5秒或19秒 C.5秒或17秒 D.7秒或19秒
3.如图,,平分,,,,有下列结论:①;②平分;③;④.其中正确结论的个数为( )
A.个 B.个 C.个 D.个
4.如图,已知,平分,平分,则下列判断:①;②平分;③;④中,正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,直线,,则的度数为( )
A. B. C. D.
6.如图,直线,三角板的直角顶点在直线上,已知,则等于( ).
A.25° B.55° C.65° D.75°
7.如图,已知平分,平分,.下列结论正确的有( )
①;②;③;④若,则.
A.1个 B.2个 C.3个 D.4个
8.如图,点在线段上,点、分别在线段、的延长线上,平分交于点,且,.则图中与相等的角有( ).
A.6个 B.5个 C.4个 D.3个
9.如图,把一个长方形纸片沿折叠后,点,分别落在,的位置,若,则等于( )
A. B. C. D.
10.如图,ADBC,∠B=∠D,延长BA至点E,连接CE,∠EAD和∠ECD的角平分线交于点P.下列三个结论:
①ABCD;②∠AOC=∠EAD+∠ECD;③若∠E=60°,∠APC=70°,则∠D=80°.其中结论正确的个数有( )
A.0 B.1 C.2 D.3
二、填空题
11.“如果a>0,b>0,那么ab>0”的逆命题是_____.
12.点A在点B的北偏东80°方向上,点C在射线BA与正北方向夹角的角平分线上,那么点C位于点A__处.
13.两个角和的两边互相平行,且角比角的2倍少30°,则这个角是____________度.
14.如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠ABC的补角,则∠BAH的度数是______.
15.如图,将一张长方形纸带沿EF折叠,点C,D的对应点分别为,,若,请直接用含的式子表示∠为____________.
三、解答题
16.已知:如图,∠BAP+∠APD=180°,∠1=∠2.求证:∠E=∠F.
17.已知,点在点的右侧,平分,平分,,相交于点,,.
(1)如图1,若点在点的左侧.
①求的度数;
②求的度数(用含的式子表示);
(2)如图2,若点在点的右侧,求的度数(用含的式子表示).
18.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,
①求∠BEC的度数;
②如图2,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
19.如图,已知:,垂足为点,,垂足为点,点在上,连接.
(1)与平行吗?为什么?
(2)若、,求的度数.
20.如图1,∠EFH=90°,点A、C分别在射线FE和FH上,AB∥CD.
(1)若∠FAB=150°,则∠HCD= °;
(2)小明同学发现:无论∠FAB如何变化,∠FAB﹣∠HCD的值始终为定值,并给出了一种证明该发现的辅助线作法:如图2,过A作AM∥FH,交CD于M,请你根据小明同学提供的辅助线(或自己添加其它辅助线),先确定该定值,并说明理由;
(3)如图3,把“∠EFH=90°”改为“∠EFH=120°”,其它条件保持不变,猜想∠FAB与∠HCD的数量关系,并说明理由.
21.如图,已知四边形ABCD中,∠A=106°﹣α,∠ABC=74°+α,BD⊥DC于D,EF⊥DC于F,求证:∠1=∠2.
22.如图,点A在直线PQ上,点C在直线MN上,PQ∥MN,∠CAQ=60°,CB平分∠ACM.(作答过程不需要写依据)
(1)∠MCB= ;
(2)将∠ACB绕点C以每秒3°的速度顺时针方向旋转,A的对应点为A1,B的对应点为B1,设旋转时间为t(t<50),当2∠ACB1+∠A1CN=100°时,求旋转时间t的值;
(3)将射线CB绕点C以每秒2°的速度顺时针方向旋转,射线AQ绕点A以每秒10°的速度顺时针方向旋转,设旋转时间为m(m<40),当BC与AQ平行或垂直时,直接写出旋转时间m的值.
23.如图1,,,.求的度数.小明的思路是:过作,通过平行线的性质来求.
(1)按小明的思路,易求得的度数为______度;
(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.
【参考答案】
1.D 2.D 3.C 4.B 5.B 6.C 7.C 8.B 9.B 10.D
11.如果ab>0,那么a>0,b>0
12.北偏东40°
13.或
14.60°
15.
16.证明:∵∠BAP+∠APD=180°
∴AB//CD.(同旁内角互补两直线平行),
∴∠BAP=∠APC(两直线平行,内错角相等),
∵∠1=∠2(已知)
由等式的性质得:
∴∠BAP ∠1=∠APC ∠2,
即∠EAP=∠FPA,
∴AE//FP(内错角相等,两直线平行),
∴∠E=∠F(由两直线平行,内错角相等),
17.(1)①AB//CD,∠ADC=70°,
∴∠BAD=70°;
②如图1,过点E作EF//AB,
∵AB//CD,
∴AAB//CD//EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=n°+35°;
(2)如图2,过点E作EF//AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB//CD,
∴AB//CD//EF,
∴∠BEF=180° ∠ABE=180° n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180° n°+35°=215° n°.
18.(1)证明:∵DE∥BC,
∴∠ADE=∠ABC,
∵∠BCF+∠ADE=180°,
∴∠BCF+∠ABC=180°,
∴CF∥AB;
(2)①解:如图,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
②∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG-∠EBC=40°-28°=12°.
19.(1)理由如下:
∵,
∴
∴(同位角相等,两直线平行)
(2)∵
∴(两直线平行,同位角相等)
∵
∴
∴(内错角相等,两直线平行)
∴(两直线平行,同位角相等)
20.解:(1)如图,过点F作FG∥AB,
∵FG∥AB,∠FAB=150°,
∴∠AFG+∠FAB=180°,
∴∠AFG=180°﹣∠FAB=180°﹣150°=30°,
∵∠EFH=90°,
∴∠CFG=∠EFH﹣∠AFG=90°﹣30°=60°,
∵AB∥CD,
∴FG∥CD,
∴∠HCD=∠CFG=60°,
故答案为:60°;
(2)∠FAB﹣∠HCD=90°,理由如下:
∵AM∥FH,∠EFH=90°,
∴∠EFH+∠FAM=180°,∠HCD=∠AMC,
∴∠FAM=180°﹣∠EFH=180°﹣90°=90°,
∵AB∥CD,
∴∠BAM=∠AMC,
∴∠HCD=∠BAM,
∴∠FAB﹣∠HCD=∠FAB﹣∠BAM=∠FAM=90°,
∴无论∠FAB如何变化,∠FAB﹣∠HCD的值始终为定值90°;
(3)∠FAB﹣∠HCD=60°,理由如下:
如图,过点A作AN∥FH交CD于点N,
∵AN∥FH,∠EFH=120°,
∴∠EFH+∠FAN=180°,∠HCD=∠ANC,
∴∠FAN=180°﹣∠EFH=180°﹣120°=60°,
∵AB∥CD,
∴∠BAN=∠ANC,
∴∠BAN=∠HCD,
∴∠FAB﹣∠HCD=∠FAB﹣∠BAN=∠FAN=60°.
21.证明:∵∠A=106°﹣α,∠ABC=74°+α,
∴∠A+∠ABC=180°,
∴AD∥BC,
∴∠1=∠DBC,
∵BD⊥DC,EF⊥DC,
∴∠BDC=∠EFC=90°,
∴BD∥EF,
∴∠2=∠DBC,
∴∠1=∠2.
22.解:(1)∵PQ∥MN,∠CAQ=60°,
∴∠ACM=∠CAQ=60°.
又∵CB平分∠ACM,
∴∠MCB=30°.
故答案为:30°.
(2)∵t<50,
∴可旋转的度数3×50=150°<180°,即B不会运动到直线CN上.
①当B1在A的左边时,t<30÷3=10,∠ACN=120°,
∴∠ACB1=30﹣3t,∠A1CN=120﹣3t
又∵2∠ACB1+∠A1CN=100°,
∴2(30﹣3t)+120﹣3t=100,
∴t=.
②当A1和B1在∠ACN之间时,10≤t≤40,
∴∠ACB1=3t﹣30,∠A1CN=120﹣3t.
又∵2∠ACB1+∠A1CN=100°,
∴2(3t﹣30)+120﹣3t=100,
∴t=.
③当B1在∠ACN之间,A1在直线CN下方时,40<t<50,
∴∠ACB1=3t﹣30,∠A1CN=3t﹣120.
又∵2∠ACB1+∠A1CN=100°,
∴2(3t﹣30)+3t﹣120=100,
∴t=(舍去).
∴综上所述,t的取值为或;
(3)∵m<40,
∴当BC∥AQ时有两种:30+2m=10m或30+2m=10m﹣180,
解得m=3.75,26.25.
∴当BC⊥AQ时有三种情况:30+2m+10m=90,30+2m+10m=270,30+2m+10m=450,
解得m=5,12,35.
答: m的值为3.75,26.25,5,20,35.
23.解:(1)∵AB∥CD,PE∥AB,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵,,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)
理由:过作交于,
∵,
∴
∴,,
∴;
(3)①当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
②当在延长线上时,过作交于,
∵,
∴
∴,,
∴;
综上所述,
