2021—2022学年度人教版七年级数学下册5.4 平移 课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年度人教版七年级数学下册5.4 平移 课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 10:46:58 | ||
图片预览


文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线 5.4平移 课后练习
一、选择题
1.下列说法中正确的是( )
A.两条直线被第三条直线所截,内错角相等 B.平移不改变图形的形状和大小
C.平行线间的距离是夹在两平行线间的线段的长度 D.相等的角是对顶角
2.下列命题中,是真命题的是( )
A.过一点有且只有一条直线与已知直线平行 B.平移的方向一定是水平的
C.同旁内角互补 D.对顶角相等
3.关于图形平移的特征叙述,有下列两种说法:①一个图形和它经过平移所得的图形中,两组对应点的连线一定平行;②一个图形和它经过平移所得的图形中,两组对应点的连线一定相等.其中判断正确的是( )
A.①错②对 B.①对②错 C.①②都错 D.①②都对
4.如图,将直角△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③∠C=∠BHD;④阴影部分的面积为6cm2.其中正确的是( )
A.①②③④ B.②③④ C.①②③ D.①②④
5.如图,面积为2cm2的△ABC,沿BC方向平移至△DEF的位置,平移的距离是边BC长的2倍,则图中的四边形ACED 的面积为( )
A.4cm2 B.6cm2 C.8cm2 D.10cm2
6.如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移5个单位长度就得到了另一直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )
①AC∥DF;②HE=5;③CF=5;④四边形DHCF的面积为32.5.
A.1个 B.2个 C.3个 D.4个
7.如图,将向右平移得到,如果的周长是,那么四边形的周长是( )
A.16 B.18 C.20 D.21
8.如图,人民公园内一块长方形草地上原有一条宽的笔直小路,现要将这条小路改造成弯曲小路,小路的上边线向下平移就是它的下边线,那么改造后小路的面积( )
A.变大了 B.变小了 C.没变 D.无法确定
9.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘.上架设小桥,若荷塘周长为280m,且桥宽忽略不计,则小桥总长为(矩形即长方形) ( )
A.280m B.140m C.260m D.130m
10.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC、△PB′C′的面积分别为,则下列关系正确的是( )
A. B. C. D.
二、填空题
11.如图,台阶的宽度为,其高度,水平距离,要在台阶上铺满地毯,则地毯的面积为__________
12.如图,将沿方向向右平移得.若,.则__________.
13.如图,是由通过平移得到,且点在同一条直线上,如果,.那么这次平移的距离是_________.
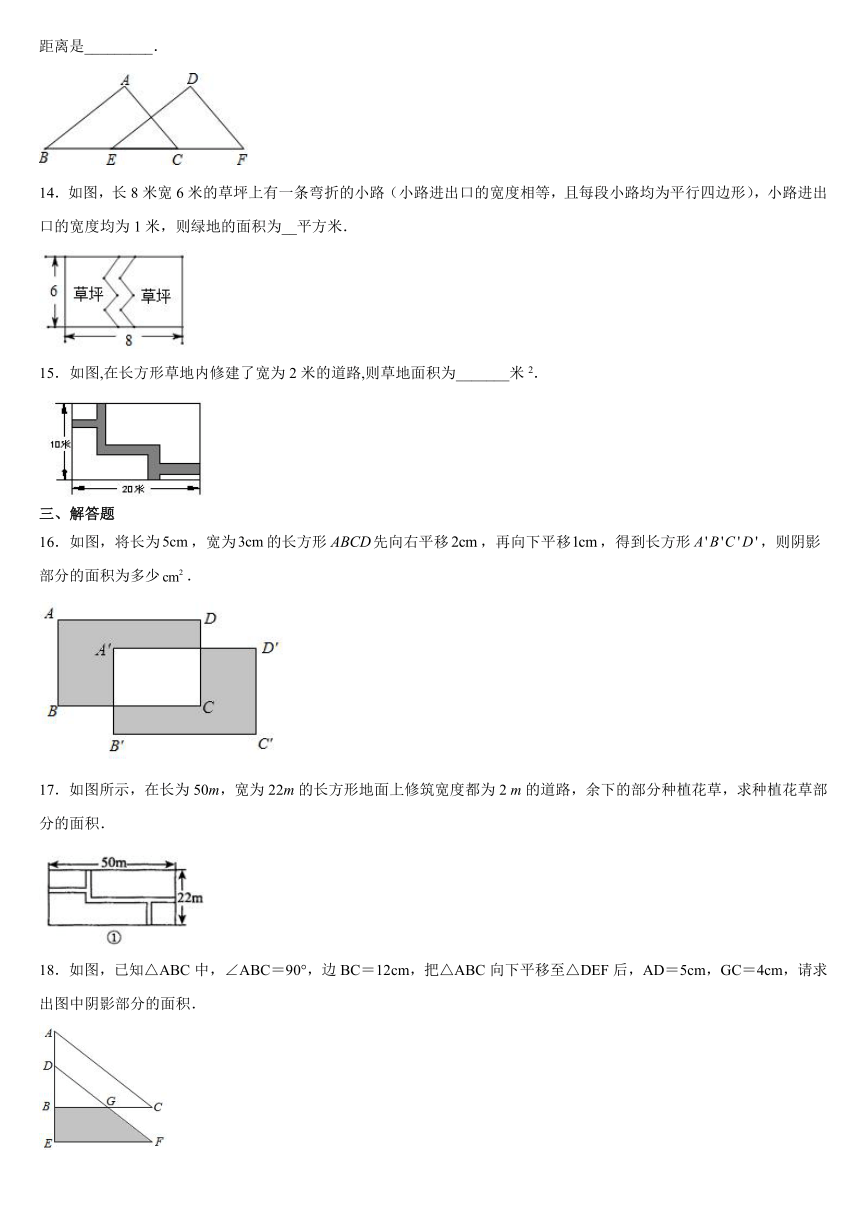
14.如图,长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等,且每段小路均为平行四边形),小路进出口的宽度均为1米,则绿地的面积为__平方米.
15.如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2.
三、解答题
16.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为多少.
17.如图所示,在长为50m,宽为22m的长方形地面上修筑宽度都为2 m的道路,余下的部分种植花草,求种植花草部分的面积.
18.如图,已知△ABC中,∠ABC=90°,边BC=12cm,把△ABC向下平移至△DEF后,AD=5cm,GC=4cm,请求出图中阴影部分的面积.
19.如图,在三角形中,,,沿方向平移至,若,.
(1)求的长;
(2)求四边形的周长.
20.如图,在中,,,将沿方向平移得到,且,.
(1)求线段的长;
(2)求四边形的周长.
21.河的两岸成平行线,A,B是位于河两岸的两个车间(如图1).要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法如下:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB,EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.
(1)分析桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.
(2)利用前一问的做法,解决下面的问题:如图2所示A、B、C三地被两条河隔开,现要修两座与河岸垂直的桥,如何修使A到B到C的路程最短?请作出示意图.
22.如图(1),已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求△ABC所扫过的图形面积;
(2)试判断,AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
23.如图,将三角形ABC沿射线BA的方向平移到三角形A'B'C'的位置,连接AC',
(1)AA'与CC'的位置关系为 ;
(2)试说明∠A'+∠CAC'+∠AC'C=180°的理由.
(3)设∠AC'B'=x,∠ACB=y,试探索∠CAC'与x、y之间的数量关系,并说明你的理由.
【参考答案】
1.B 2.D 3.A 4.A 5.B 6.D 7.C 8.C 9.B 10.C
11.15
12.4
13.4
14.42
15.144
16.18
17.960(m2)
18.50cm2
19.(1);(2)
20.(1)8;(2)31
21.(1)两点之间线段最短.(2)略.
22.(1)9;(2)BE⊥AF;(3)2.
23.(1)AA′∥CC′;(2)略;(3)∠CAC'=x+y
一、选择题
1.下列说法中正确的是( )
A.两条直线被第三条直线所截,内错角相等 B.平移不改变图形的形状和大小
C.平行线间的距离是夹在两平行线间的线段的长度 D.相等的角是对顶角
2.下列命题中,是真命题的是( )
A.过一点有且只有一条直线与已知直线平行 B.平移的方向一定是水平的
C.同旁内角互补 D.对顶角相等
3.关于图形平移的特征叙述,有下列两种说法:①一个图形和它经过平移所得的图形中,两组对应点的连线一定平行;②一个图形和它经过平移所得的图形中,两组对应点的连线一定相等.其中判断正确的是( )
A.①错②对 B.①对②错 C.①②都错 D.①②都对
4.如图,将直角△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③∠C=∠BHD;④阴影部分的面积为6cm2.其中正确的是( )
A.①②③④ B.②③④ C.①②③ D.①②④
5.如图,面积为2cm2的△ABC,沿BC方向平移至△DEF的位置,平移的距离是边BC长的2倍,则图中的四边形ACED 的面积为( )
A.4cm2 B.6cm2 C.8cm2 D.10cm2
6.如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移5个单位长度就得到了另一直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )
①AC∥DF;②HE=5;③CF=5;④四边形DHCF的面积为32.5.
A.1个 B.2个 C.3个 D.4个
7.如图,将向右平移得到,如果的周长是,那么四边形的周长是( )
A.16 B.18 C.20 D.21
8.如图,人民公园内一块长方形草地上原有一条宽的笔直小路,现要将这条小路改造成弯曲小路,小路的上边线向下平移就是它的下边线,那么改造后小路的面积( )
A.变大了 B.变小了 C.没变 D.无法确定
9.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘.上架设小桥,若荷塘周长为280m,且桥宽忽略不计,则小桥总长为(矩形即长方形) ( )
A.280m B.140m C.260m D.130m
10.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC、△PB′C′的面积分别为,则下列关系正确的是( )
A. B. C. D.
二、填空题
11.如图,台阶的宽度为,其高度,水平距离,要在台阶上铺满地毯,则地毯的面积为__________
12.如图,将沿方向向右平移得.若,.则__________.
13.如图,是由通过平移得到,且点在同一条直线上,如果,.那么这次平移的距离是_________.
14.如图,长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等,且每段小路均为平行四边形),小路进出口的宽度均为1米,则绿地的面积为__平方米.
15.如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2.
三、解答题
16.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为多少.
17.如图所示,在长为50m,宽为22m的长方形地面上修筑宽度都为2 m的道路,余下的部分种植花草,求种植花草部分的面积.
18.如图,已知△ABC中,∠ABC=90°,边BC=12cm,把△ABC向下平移至△DEF后,AD=5cm,GC=4cm,请求出图中阴影部分的面积.
19.如图,在三角形中,,,沿方向平移至,若,.
(1)求的长;
(2)求四边形的周长.
20.如图,在中,,,将沿方向平移得到,且,.
(1)求线段的长;
(2)求四边形的周长.
21.河的两岸成平行线,A,B是位于河两岸的两个车间(如图1).要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法如下:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB,EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.
(1)分析桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.
(2)利用前一问的做法,解决下面的问题:如图2所示A、B、C三地被两条河隔开,现要修两座与河岸垂直的桥,如何修使A到B到C的路程最短?请作出示意图.
22.如图(1),已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求△ABC所扫过的图形面积;
(2)试判断,AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
23.如图,将三角形ABC沿射线BA的方向平移到三角形A'B'C'的位置,连接AC',
(1)AA'与CC'的位置关系为 ;
(2)试说明∠A'+∠CAC'+∠AC'C=180°的理由.
(3)设∠AC'B'=x,∠ACB=y,试探索∠CAC'与x、y之间的数量关系,并说明你的理由.
【参考答案】
1.B 2.D 3.A 4.A 5.B 6.D 7.C 8.C 9.B 10.C
11.15
12.4
13.4
14.42
15.144
16.18
17.960(m2)
18.50cm2
19.(1);(2)
20.(1)8;(2)31
21.(1)两点之间线段最短.(2)略.
22.(1)9;(2)BE⊥AF;(3)2.
23.(1)AA′∥CC′;(2)略;(3)∠CAC'=x+y
