3.1.2函数的单调性(第1课时)课件-2021-2022学年高一数学上学期人教B版(2019)必修第一册(12张ppt)
文档属性
| 名称 | 3.1.2函数的单调性(第1课时)课件-2021-2022学年高一数学上学期人教B版(2019)必修第一册(12张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 21:59:41 | ||
图片预览



文档简介
(共12张PPT)
《3.1.2 函数的单调性》
人教版高中数学B版必修第一册
(第1课时)单调性的定义与证明
情境与问题
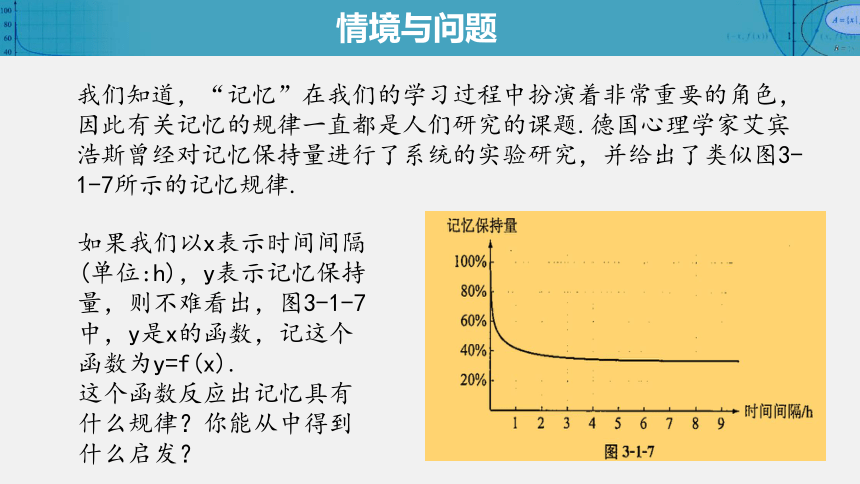
我们知道,“记忆”在我们的学习过程中扮演着非常重要的角色,因此有关记忆的规律一直都是人们研究的课题.德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究,并给出了类似图3-1-7所示的记忆规律.
如果我们以x表示时间间隔(单位:h),y表示记忆保持量,则不难看出,图3-1-7中,y是x的函数,记这个函数为y=f(x).
这个函数反应出记忆具有什么规律?你能从中得到什么启发?
情境与问题中的函数y=f(x)反应出记忆的如下规律:随着时间间隔x的增大,记忆保持量y将减小.
给定一个函数,人们有时候关心的是,函数值会随着自变量增大而怎样变化,类似的内容我们在初中曾经接触过.
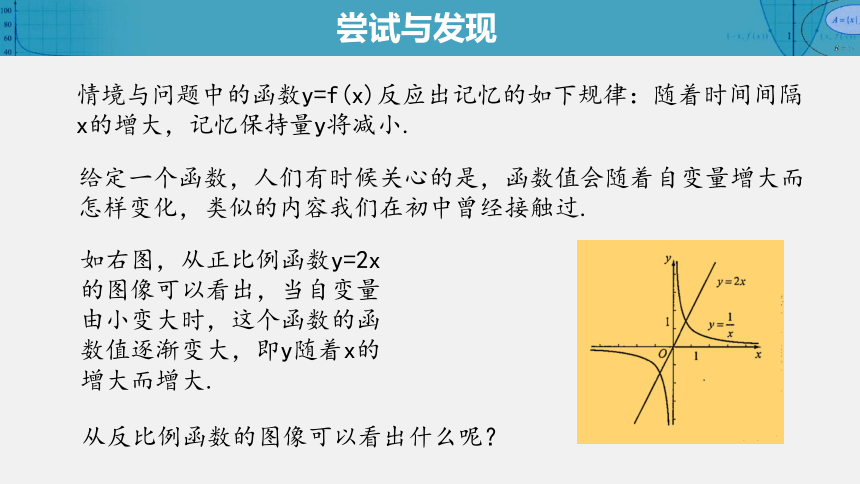
如右图,从正比例函数y=2x的图像可以看出,当自变量由小变大时,这个函数的函数值逐渐变大,即y随着x的增大而增大.
从反比例函数的图像可以看出什么呢?
尝试与发现
概念形成
思考与讨论
能否说 在定义域内是减函数?
尝试与发现
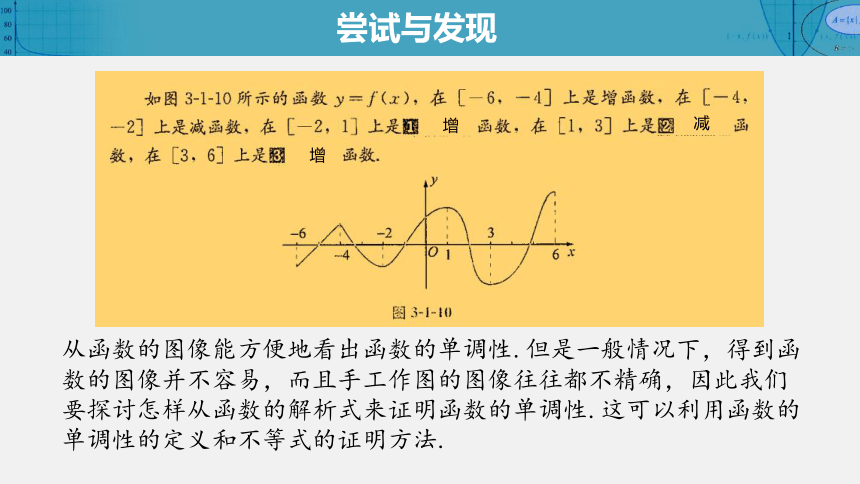
从函数的图像能方便地看出函数的单调性.但是一般情况下,得到函数的图像并不容易,而且手工作图的图像往往都不精确,因此我们要探讨怎样从函数的解析式来证明函数的单调性.这可以利用函数的单调性的定义和不等式的证明方法.
增
增
减
例1.判断并证明函数 的单调性.
证明:任取
所以,函数 为增函数.
典例讲解
概念形成
函数的最值
典例讲解
例2.判断函数 的单调性,并求这个函数的最值.
解:任取 且 ,则
那么
所以这个函数是增函数
因此,当 时,有
从而这个函数的最小值为
最大值为
课堂小结
1.知识总结:单调性的概念;单调性证明的步骤.
2.方法总结:函数的性质不仅能够从图中得到,也可从函数解析式中得到,关注函数解析式给予的信息,利于了解函数性质.
布置作业
课本第102页练习A:2、4、5、6.
谢
谢
看
观
谢
谢
看
观
谢
谢
看
观
《3.1.2 函数的单调性》
人教版高中数学B版必修第一册
(第1课时)单调性的定义与证明
情境与问题
我们知道,“记忆”在我们的学习过程中扮演着非常重要的角色,因此有关记忆的规律一直都是人们研究的课题.德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究,并给出了类似图3-1-7所示的记忆规律.
如果我们以x表示时间间隔(单位:h),y表示记忆保持量,则不难看出,图3-1-7中,y是x的函数,记这个函数为y=f(x).
这个函数反应出记忆具有什么规律?你能从中得到什么启发?
情境与问题中的函数y=f(x)反应出记忆的如下规律:随着时间间隔x的增大,记忆保持量y将减小.
给定一个函数,人们有时候关心的是,函数值会随着自变量增大而怎样变化,类似的内容我们在初中曾经接触过.
如右图,从正比例函数y=2x的图像可以看出,当自变量由小变大时,这个函数的函数值逐渐变大,即y随着x的增大而增大.
从反比例函数的图像可以看出什么呢?
尝试与发现
概念形成
思考与讨论
能否说 在定义域内是减函数?
尝试与发现
从函数的图像能方便地看出函数的单调性.但是一般情况下,得到函数的图像并不容易,而且手工作图的图像往往都不精确,因此我们要探讨怎样从函数的解析式来证明函数的单调性.这可以利用函数的单调性的定义和不等式的证明方法.
增
增
减
例1.判断并证明函数 的单调性.
证明:任取
所以,函数 为增函数.
典例讲解
概念形成
函数的最值
典例讲解
例2.判断函数 的单调性,并求这个函数的最值.
解:任取 且 ,则
那么
所以这个函数是增函数
因此,当 时,有
从而这个函数的最小值为
最大值为
课堂小结
1.知识总结:单调性的概念;单调性证明的步骤.
2.方法总结:函数的性质不仅能够从图中得到,也可从函数解析式中得到,关注函数解析式给予的信息,利于了解函数性质.
布置作业
课本第102页练习A:2、4、5、6.
谢
谢
看
观
谢
谢
看
观
谢
谢
看
观
