人教版八年级数学下册16章《二次根式》复习课件 (共33张PPT)
文档属性
| 名称 | 人教版八年级数学下册16章《二次根式》复习课件 (共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 520.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 16:09:44 | ||
图片预览




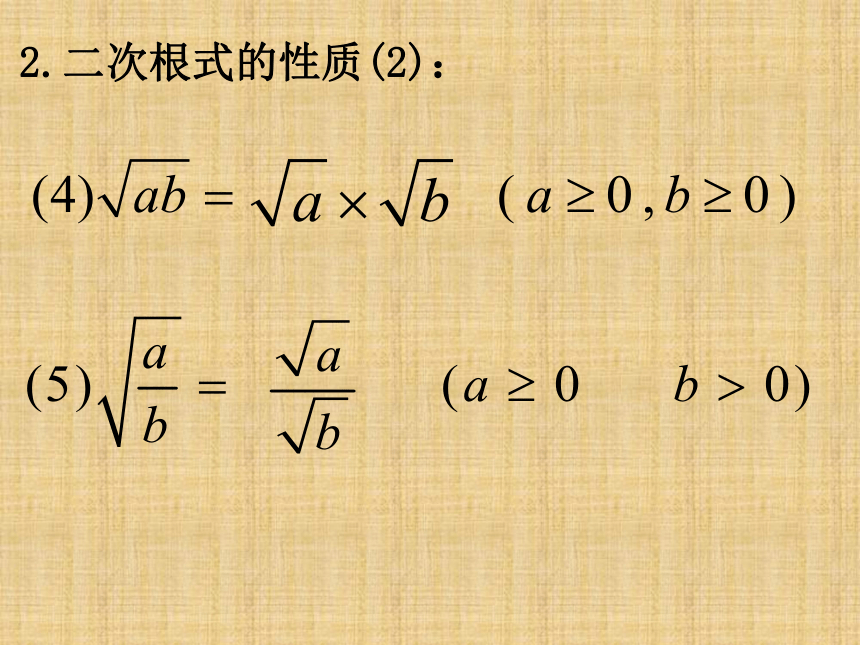





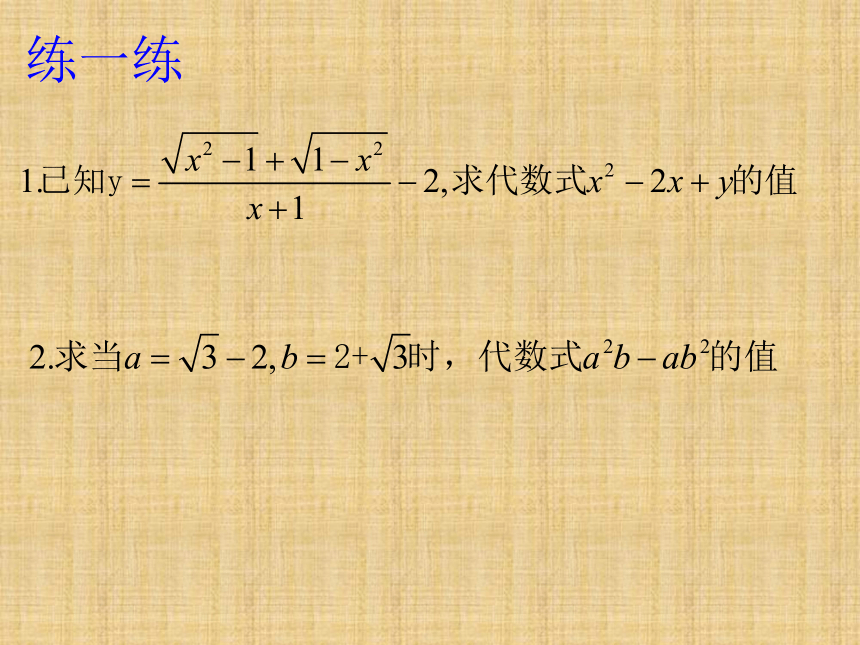

文档简介
(共33张PPT)
§16 二 次 根 式
复习
(1)形如 的 式子叫做二次根式.
(即一个 的算术平方根叫做二次根式)
本章知识
非负数
1.二次根式的有关概念:
(1)二次根式(2)最简二次根式(3)同类二次根式
注意:
二次根式有意义的条件:
被开方数大于或等于零
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式;
(2)满足下列两个条件的二次根式,叫做最简二次根式:
(3)几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式。
若 则 ;
注:若 则 ;
2.二次根式的性质(1):
(1) 非负性 :
2.二次根式的性质(2):
3.二次根式的运算:
二次根式乘法法则
二次根式除法法则
二次根式的加减:
类似于合并同类项,关键是把同类二次根式合并。
二次根式的混合运算:
原来学习的运算律(结合律、交换律、分配律)仍然适用,
原来所学的乘法公式(如 ,
)仍然适用。
1.当x取何值时,下列二次根式有意义:
①
②
③
④
⑤
⑥
⑦
⑧
题型1:二次根式有意义的条件
3.
有意义的条件是______
2. 当 _____时, 有意义。
4.求下列二次根式中字母的取值范围
解:
①
②
≤3
a=4
说明:二次根式被开方数大于等于0,所以求二次根式中字母的取值范围常转化为不等式(组)
解得
5.在实数范围内分解因式.
(1)x2-7 (2)x4-9
变式训练
练一练
2.(2005.湖北黄冈市)已知x,y为实数,且
,则 的值为( )
A.3 B.-3 C.1 D.-1
题型2:二次根式的非负性的应用
D
1.已知: ,求 的值.
解得
解:由题意,得
题型3:化简
把下列二次根化为最简二次根式
变式应用
1.式子 成立的条件是( )
D
题型4:同类二次根式
1.下列与
是同类二次根式的有:( )
B.
C.
D.
A.
2.下列与
不是同类二次根式的有:( )
B.
C.
D.
A.
(题中 )
B
D
题型5: 计算
题型6
1.如图,四边形ABCD中,∠A=∠BCD=Rt∠,已知∠B=450,
AB= CD=
求(1)四边形ABCD的周长;
(2)四边形ABCD的面积。
A
B
C
D
例1 解方程:
解:
在直角坐标系中,点P(1, )到原点的距离是_________
2
P
例2
O
x
y
例3 一个台阶如图,阶梯每一层高15cm,宽25cm,长60cm.一只蚂蚁从A点爬到B点最短路程是多少?
25
15
15
25
60
60
A
B
解:
B
15
15
25
25
60
60
A
设a.b为实数,且
解: (1)
求 的值
(1)
(2) 若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的面积.
解:(2) 若a为腰,b为底,此时底边上的高为
若a为底,b为腰,此时底边上的高为
∴三角形的面积为
∴三角形的面积为
例、 求代数式的值.
若x2-4x+1=0,求 的值.
解:
(1)由x2-4x+1=0 x+ =4.
∴原式=
D
x≤0
D
说明:注意二次根式中字母的取值条件.
5.请计算
的值
将根号内的3换成其他正数,结果怎样?
你能从计算中发现什么运算规律?(请用文字描述或用字母标示出来)
6、比较根式的大小.
解:
应用练习
7、化简:
(2) + +
+…+ = .
例、(1)设a、b、c为△ABC的三边,试化简:
二次根式的拓展提高
(2)设 的整数部分为a,小数
部分为b.求 的值。
A
B
P
D
C
若点P为线段CD上动点。
已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C,
①则AD=____ BC=____
1
2
(1)在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为
拓展3
② 设DP=a,请用含a的代数式表示AP,BP。则AP=__________,BP=__________。
③ 当a=1 时,则PA+PB=______,
当a=3,则PA+PB=______
④ PA+PB是否存在一个最小值?
细心观察图形,认真分析,思考下列问题.
(1)求出各条线段的长和各个三角形的面积。
A2
1
1
1
1
1
1
1
1
S1
S2
S3
S4
S5
S6
O
A3
A4
A5
A6
A7
A1
OA2=___
OA3=___
……
OAn=___
S1=___
S2=___
……
Sn=___
试一试
(2)请计算
S1= S2= …Sn=
A2
1
1
1
1
1
1
1
1
S1
S2
S3
S4
S5
S6
O
A3
A4
A5
A6
A7
A1
§16 二 次 根 式
复习
(1)形如 的 式子叫做二次根式.
(即一个 的算术平方根叫做二次根式)
本章知识
非负数
1.二次根式的有关概念:
(1)二次根式(2)最简二次根式(3)同类二次根式
注意:
二次根式有意义的条件:
被开方数大于或等于零
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式;
(2)满足下列两个条件的二次根式,叫做最简二次根式:
(3)几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式。
若 则 ;
注:若 则 ;
2.二次根式的性质(1):
(1) 非负性 :
2.二次根式的性质(2):
3.二次根式的运算:
二次根式乘法法则
二次根式除法法则
二次根式的加减:
类似于合并同类项,关键是把同类二次根式合并。
二次根式的混合运算:
原来学习的运算律(结合律、交换律、分配律)仍然适用,
原来所学的乘法公式(如 ,
)仍然适用。
1.当x取何值时,下列二次根式有意义:
①
②
③
④
⑤
⑥
⑦
⑧
题型1:二次根式有意义的条件
3.
有意义的条件是______
2. 当 _____时, 有意义。
4.求下列二次根式中字母的取值范围
解:
①
②
≤3
a=4
说明:二次根式被开方数大于等于0,所以求二次根式中字母的取值范围常转化为不等式(组)
解得
5.在实数范围内分解因式.
(1)x2-7 (2)x4-9
变式训练
练一练
2.(2005.湖北黄冈市)已知x,y为实数,且
,则 的值为( )
A.3 B.-3 C.1 D.-1
题型2:二次根式的非负性的应用
D
1.已知: ,求 的值.
解得
解:由题意,得
题型3:化简
把下列二次根化为最简二次根式
变式应用
1.式子 成立的条件是( )
D
题型4:同类二次根式
1.下列与
是同类二次根式的有:( )
B.
C.
D.
A.
2.下列与
不是同类二次根式的有:( )
B.
C.
D.
A.
(题中 )
B
D
题型5: 计算
题型6
1.如图,四边形ABCD中,∠A=∠BCD=Rt∠,已知∠B=450,
AB= CD=
求(1)四边形ABCD的周长;
(2)四边形ABCD的面积。
A
B
C
D
例1 解方程:
解:
在直角坐标系中,点P(1, )到原点的距离是_________
2
P
例2
O
x
y
例3 一个台阶如图,阶梯每一层高15cm,宽25cm,长60cm.一只蚂蚁从A点爬到B点最短路程是多少?
25
15
15
25
60
60
A
B
解:
B
15
15
25
25
60
60
A
设a.b为实数,且
解: (1)
求 的值
(1)
(2) 若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的面积.
解:(2) 若a为腰,b为底,此时底边上的高为
若a为底,b为腰,此时底边上的高为
∴三角形的面积为
∴三角形的面积为
例、 求代数式的值.
若x2-4x+1=0,求 的值.
解:
(1)由x2-4x+1=0 x+ =4.
∴原式=
D
x≤0
D
说明:注意二次根式中字母的取值条件.
5.请计算
的值
将根号内的3换成其他正数,结果怎样?
你能从计算中发现什么运算规律?(请用文字描述或用字母标示出来)
6、比较根式的大小.
解:
应用练习
7、化简:
(2) + +
+…+ = .
例、(1)设a、b、c为△ABC的三边,试化简:
二次根式的拓展提高
(2)设 的整数部分为a,小数
部分为b.求 的值。
A
B
P
D
C
若点P为线段CD上动点。
已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C,
①则AD=____ BC=____
1
2
(1)在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为
拓展3
② 设DP=a,请用含a的代数式表示AP,BP。则AP=__________,BP=__________。
③ 当a=1 时,则PA+PB=______,
当a=3,则PA+PB=______
④ PA+PB是否存在一个最小值?
细心观察图形,认真分析,思考下列问题.
(1)求出各条线段的长和各个三角形的面积。
A2
1
1
1
1
1
1
1
1
S1
S2
S3
S4
S5
S6
O
A3
A4
A5
A6
A7
A1
OA2=___
OA3=___
……
OAn=___
S1=___
S2=___
……
Sn=___
试一试
(2)请计算
S1= S2= …Sn=
A2
1
1
1
1
1
1
1
1
S1
S2
S3
S4
S5
S6
O
A3
A4
A5
A6
A7
A1
