人教版八年级数学下册课件:第16章二次根式复习课(课时2)课件 (共30张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:第16章二次根式复习课(课时2)课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 872.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 18:10:42 | ||
图片预览








文档简介
(共30张PPT)
第十六章 二次根式复习
第2 课时
知识梳理
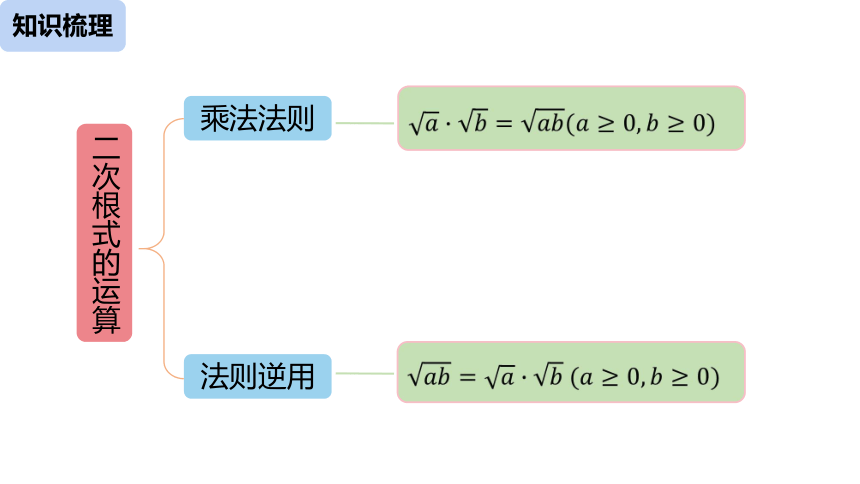
二次根式的运算
乘法法则
法则逆用
知识梳理
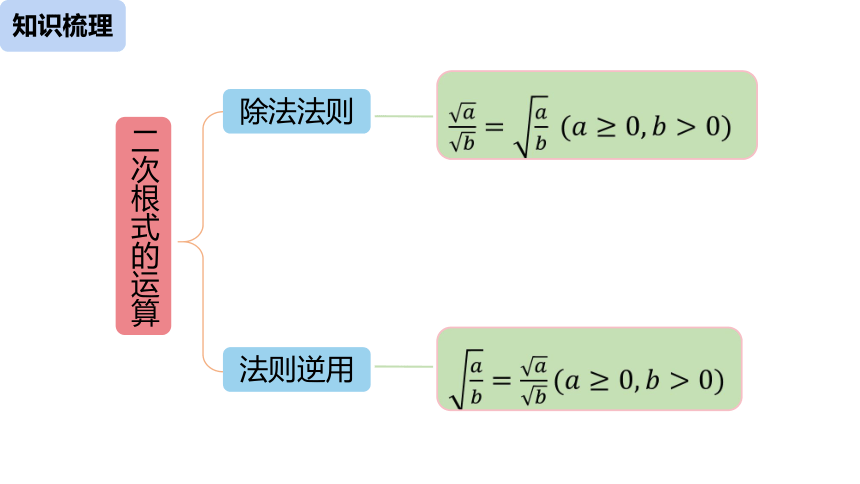
二次根式的运算
除法法则
法则逆用
知识梳理
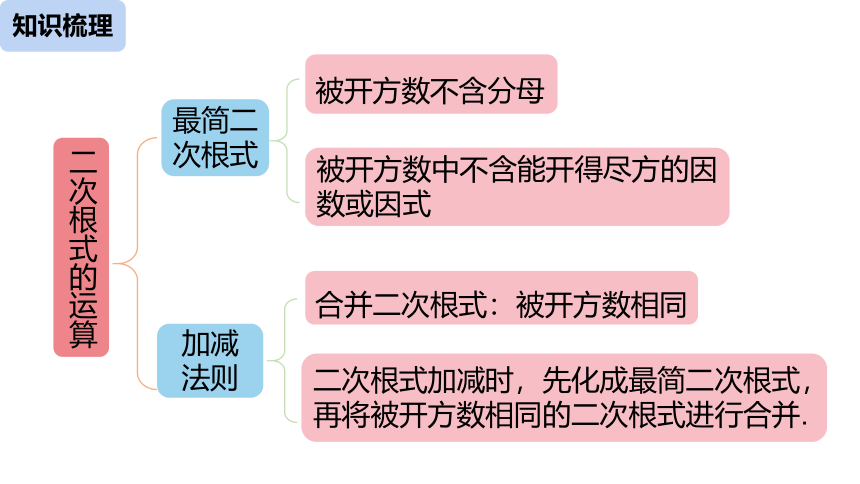
二次根式的运算
最简二次根式
被开方数不含分母
被开方数中不含能开得尽方的因数或因式
加减
法则
合并二次根式:被开方数相同
二次根式加减时,先化成最简二次根式,再将被开方数相同的二次根式进行合并.
知识梳理
二次根式的运算
混合
运算
加、减、乘、除、乘方、开方混合
先乘方,再乘除,最后加减,有括号的先去掉括号.
灵活运用运算律、多项式乘法法则和乘法公式.
知识梳理
1.二次根式的乘法法则
文字表述:二次根式相乘,把 相乘, 不变.
被开方数
根指数
知识梳理
文字表述:积的算术平方根等于积中各个因数或因式的算术平方根的积.
1.二次根式的乘法法则
知识梳理
2.二次根式的除法法则
文字表述:二次根式相除,把 相除, 不变.
被开方数
根指数
法则: (a≥0,b>0).
拓展:
知识梳理
2.二次根式的除法法则
文字表述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根 .
法则逆用: (a≥0,b>0).
知识梳理
3. 最简二次根式
最简二次根式:满足以下两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式 .
知识梳理
4. 二次根式的加减
二次根式的加减:一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
可以合并的二次根式:将二次根式化成 ,若
,则这样的二次根式可以 .
最简二次根式
被开方数相同
合并
知识梳理
5. 二次根式的混合运算
二次根式的混合运算种类:二次根式的加、减、乘、除、乘方(或开方)的混合运算.
二次根式的混合运算顺序:先乘方,再乘除,最后加减,有括号的先算括号里面的(或先去掉括号).与整式的混合运算顺序相同.
二次根式的混合运算依据:有理数的运算律、多项式乘法法则和乘法公式.
重点解析
重难点1:二次根式的乘法法则
1.计算下列式子:
重点解析
1.计算下列式子:
将二次根式下的带分数化为假分数.
重点解析
2.化简下列各式子:
重点解析
2.化简下列各式子:
重点解析
重难点2:二次根式的除法法则
1.计算下列式子:
将二次根式下的带分数化为假分数
重点解析
2.化简下列各式子:
重点解析
重难点3:最简二次根式
把下列二次根式化成最简二次根式:
重点解析
重难点4:二次根式的加减法
计算下列式子:
重点解析
重难点5:二次根式的混合运算
计算下列式子:
重点解析
计算下列式子:
深化练习
1.计算:
深化练习
二次根式乘除混合运算的方法
(1)将式子中的除法转化为乘法;
(2)利用乘法运算律转化为系数和被开方数的运算;
(3)将系数和被开方数分别相乘;
(4)结果化成最简二次根式(或整式).
深化练习
利用完全平方公式和平方差公式进行运算.
深化练习
深化练习
解析:本题可以采用“0”点取值法,即令要讨论的每个代数值为 0,求出代数式的值为 0 时字母的值,然后进行分类讨论.分类讨论时要做到不重复、不遗漏.
深化练习
深化练习
深化练习
综上可知,原式=
第十六章 二次根式复习
第2 课时
知识梳理
二次根式的运算
乘法法则
法则逆用
知识梳理
二次根式的运算
除法法则
法则逆用
知识梳理
二次根式的运算
最简二次根式
被开方数不含分母
被开方数中不含能开得尽方的因数或因式
加减
法则
合并二次根式:被开方数相同
二次根式加减时,先化成最简二次根式,再将被开方数相同的二次根式进行合并.
知识梳理
二次根式的运算
混合
运算
加、减、乘、除、乘方、开方混合
先乘方,再乘除,最后加减,有括号的先去掉括号.
灵活运用运算律、多项式乘法法则和乘法公式.
知识梳理
1.二次根式的乘法法则
文字表述:二次根式相乘,把 相乘, 不变.
被开方数
根指数
知识梳理
文字表述:积的算术平方根等于积中各个因数或因式的算术平方根的积.
1.二次根式的乘法法则
知识梳理
2.二次根式的除法法则
文字表述:二次根式相除,把 相除, 不变.
被开方数
根指数
法则: (a≥0,b>0).
拓展:
知识梳理
2.二次根式的除法法则
文字表述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根 .
法则逆用: (a≥0,b>0).
知识梳理
3. 最简二次根式
最简二次根式:满足以下两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式 .
知识梳理
4. 二次根式的加减
二次根式的加减:一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
可以合并的二次根式:将二次根式化成 ,若
,则这样的二次根式可以 .
最简二次根式
被开方数相同
合并
知识梳理
5. 二次根式的混合运算
二次根式的混合运算种类:二次根式的加、减、乘、除、乘方(或开方)的混合运算.
二次根式的混合运算顺序:先乘方,再乘除,最后加减,有括号的先算括号里面的(或先去掉括号).与整式的混合运算顺序相同.
二次根式的混合运算依据:有理数的运算律、多项式乘法法则和乘法公式.
重点解析
重难点1:二次根式的乘法法则
1.计算下列式子:
重点解析
1.计算下列式子:
将二次根式下的带分数化为假分数.
重点解析
2.化简下列各式子:
重点解析
2.化简下列各式子:
重点解析
重难点2:二次根式的除法法则
1.计算下列式子:
将二次根式下的带分数化为假分数
重点解析
2.化简下列各式子:
重点解析
重难点3:最简二次根式
把下列二次根式化成最简二次根式:
重点解析
重难点4:二次根式的加减法
计算下列式子:
重点解析
重难点5:二次根式的混合运算
计算下列式子:
重点解析
计算下列式子:
深化练习
1.计算:
深化练习
二次根式乘除混合运算的方法
(1)将式子中的除法转化为乘法;
(2)利用乘法运算律转化为系数和被开方数的运算;
(3)将系数和被开方数分别相乘;
(4)结果化成最简二次根式(或整式).
深化练习
利用完全平方公式和平方差公式进行运算.
深化练习
深化练习
解析:本题可以采用“0”点取值法,即令要讨论的每个代数值为 0,求出代数式的值为 0 时字母的值,然后进行分类讨论.分类讨论时要做到不重复、不遗漏.
深化练习
深化练习
深化练习
综上可知,原式=
