人教版八年级下册数学课件:第十六章二次根式复习课 课件(共25张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:第十六章二次根式复习课 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 722.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 18:16:38 | ||
图片预览






文档简介
(共25张PPT)
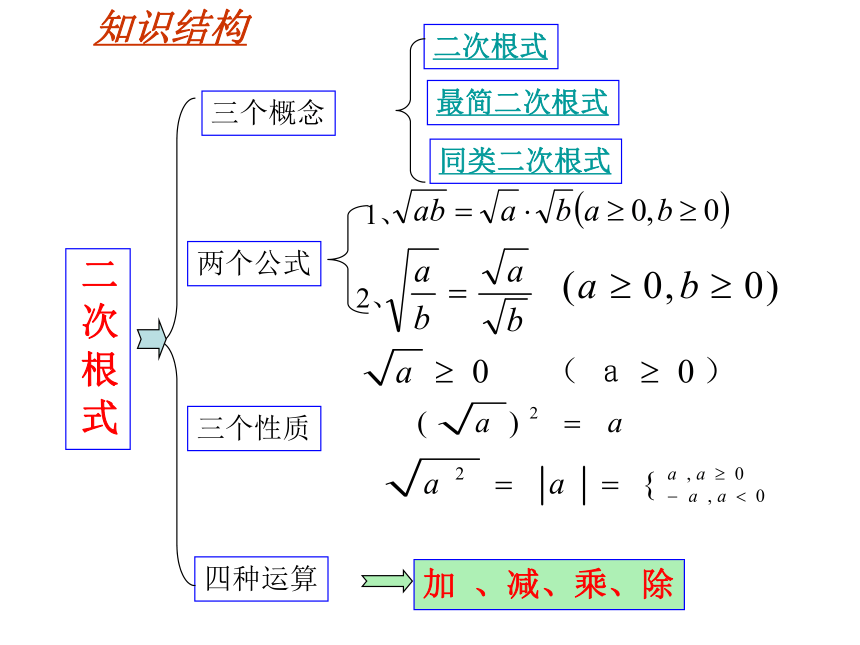
二 次 根 式
三个概念
两个公式
三个性质
四种运算
二次根式
最简二次根式
同类二次根式
1、
2、
加 、减、乘、除
知识结构
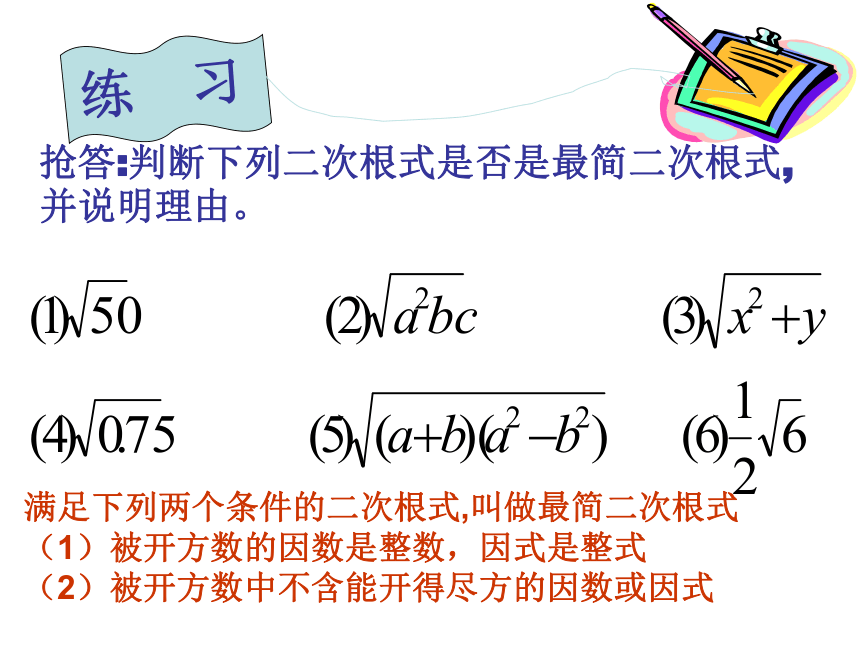
练 习
抢答:判断下列二次根式是否是最简二次根式,并说明理由。
满足下列两个条件的二次根式,叫做最简二次根式
(1)被开方数的因数是整数,因式是整式
(2)被开方数中不含能开得尽方的因数或因式
2.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
4.如果最简二次根式 与 是同类二次根式,求m、n 的值.
B
125
3. 与 是同类二次根式的是( )
A. B. C. D.
D
1.
二次根式的性质
归纳
2.从取值范围来看,
a≥0
a取任何实数
1:从运算顺序来看,
先开方,后平方
先平方,后开方
3.从运算结果来看:
= a
a (a≥ 0)
-a (a≤0)
=
=∣a∣
1.求下列二次根式中字母X的取值范围:
题型1:确定二次根式中被开方数所含字母的取值范围.
2. +
有意义的条件是 .
3、 ,则ab= .
1
a=4
题型2:二次根式的非负性的应用
4.已知: + =0,则x+y= .
4
.
1
练习:计算
题型:二次根式的性质的应用.
3实数p在数轴上的位置如图所示,化简
交流讨论:
题型:二次根式的性质的应用.
二次根式的运算
在二次根式的运算中,最后结果一般要求
(1)分母中不含有二次根式.
(2) 最后结果中的二次根式要求写成最简的二次根式的形式.
例1:
练习:计算
①
②
③
④
⑤
④
化简下列各式
÷
②
①
③
(四)二次根式的运算
①
②
③
④
练 习
2、二次根式加减运算的步骤:
(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.
(3)不是同类二次根式的不能合并.
计算
1、注意运算顺序
2、运用运算律
整式运算的运算律在
二次根式的运算中仍然适应.
B
A
(1)下列各式不是二次根式的是( )
(3)选择:下列计算正确的是( )
( )
( )
C
C
3、实数在数轴上的位置如图示,
化简|a-1|+
。
4、请计算a= , b= ,
求 a2b-ab2 的值
C
4.在函数 中,自变量x的取值范围是 ( )
A.x ≥4 B. x ≤4 C. x >4 D. x <4
1、二次根式 有意义,则x的取值范围是
2、二次根式 的值是( )
A、-3 B、3或-3 C、9 D、3
x≥-1
D
3、 +
有意义的条件是 __ .
二 次 根 式
三个概念
两个公式
三个性质
四种运算
二次根式
最简二次根式
同类二次根式
1、
2、
加 、减、乘、除
知识结构
练 习
抢答:判断下列二次根式是否是最简二次根式,并说明理由。
满足下列两个条件的二次根式,叫做最简二次根式
(1)被开方数的因数是整数,因式是整式
(2)被开方数中不含能开得尽方的因数或因式
2.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
4.如果最简二次根式 与 是同类二次根式,求m、n 的值.
B
125
3. 与 是同类二次根式的是( )
A. B. C. D.
D
1.
二次根式的性质
归纳
2.从取值范围来看,
a≥0
a取任何实数
1:从运算顺序来看,
先开方,后平方
先平方,后开方
3.从运算结果来看:
= a
a (a≥ 0)
-a (a≤0)
=
=∣a∣
1.求下列二次根式中字母X的取值范围:
题型1:确定二次根式中被开方数所含字母的取值范围.
2. +
有意义的条件是 .
3、 ,则ab= .
1
a=4
题型2:二次根式的非负性的应用
4.已知: + =0,则x+y= .
4
.
1
练习:计算
题型:二次根式的性质的应用.
3实数p在数轴上的位置如图所示,化简
交流讨论:
题型:二次根式的性质的应用.
二次根式的运算
在二次根式的运算中,最后结果一般要求
(1)分母中不含有二次根式.
(2) 最后结果中的二次根式要求写成最简的二次根式的形式.
例1:
练习:计算
①
②
③
④
⑤
④
化简下列各式
÷
②
①
③
(四)二次根式的运算
①
②
③
④
练 习
2、二次根式加减运算的步骤:
(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.
(3)不是同类二次根式的不能合并.
计算
1、注意运算顺序
2、运用运算律
整式运算的运算律在
二次根式的运算中仍然适应.
B
A
(1)下列各式不是二次根式的是( )
(3)选择:下列计算正确的是( )
( )
( )
C
C
3、实数在数轴上的位置如图示,
化简|a-1|+
。
4、请计算a= , b= ,
求 a2b-ab2 的值
C
4.在函数 中,自变量x的取值范围是 ( )
A.x ≥4 B. x ≤4 C. x >4 D. x <4
1、二次根式 有意义,则x的取值范围是
2、二次根式 的值是( )
A、-3 B、3或-3 C、9 D、3
x≥-1
D
3、 +
有意义的条件是 __ .
