26.1 反比例函数 同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级下 26.1反比例函数同步练习
一.选择题
1.(2021秋 揭西县期末)下列关系式中y是x的反比例函数的是( )
A.y=5x B. C. D.xy=3
2.(2021秋 徐汇区校级期末)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
3.(2021秋 南海区期末)已知反比例函数经过点A(3,2)、B(﹣1,m),则m的值为( )
A.﹣6 B. C. D.6
4.(2021秋 运城期末)点A(﹣3,y1),B(1,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y1>y3>y2 C.y2>y2>y1 D.y3>y1>y2
5.(2021秋 徐汇区期末)如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,﹣4),那么另一个交点的坐标为( )
A.(﹣3,﹣4) B.(3,4) C.(﹣3,4) D.(﹣4,3)
6.(2021秋 大同期末)已知点A(3,﹣4)在反比例函数y=的图象上,则下列说法正确的是( )
A.图象位于第一、三象限 B.点(2,6)在该函数图象上
C.当x<0时,y随x的增大而增大 D.当y≥﹣4时,x≥3
7.(2021秋 市中区期末)如图,关于x的函数y=﹣(k≠0)和y=kx﹣k,它们在同一坐标系内的图象大致是( )
A.B. C. D.
8.(2021秋 金牛区期末)如图,一次函数y=kx+b(k≠0)图象与反比例函数y=(m≠0)图象交于点A(﹣1,2),B(2,﹣1),则不等式kx+b<的解集是( )
A.x<﹣1或x>2 B.﹣1<x<0或0<x<2 C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
9.(2021秋 鸡冠区校级期末)如图,已知反比例函数y=(x>0)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为3,则k的值为( )
A.6 B.12 C.﹣3 D.﹣6
10.(2021秋 和平区期末)如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△OAQ的面积为S2,若S1+S2=3,则k的值为( )
A.2 B.1 C.﹣1 D.﹣2
二.填空题
11.(2021秋 鸡冠区校级期末)已知函数y=(m+2)x|m|﹣3是关于x的反比例函数,则实数m的值是 .
12.(2021秋 正定县期末)已知反比例函数y=的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是 .
13.(2021秋 蓬江区期末)如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣2的图象交于点P(a,b),则代数式的值为 .
14.(2021秋 仙居县期末)已知反比例函数y=,若y>﹣1,则x的取值范围是 .
15.(2021秋 海淀区校级期末)对于函数y=图象上任意两点A(x1,y1),B(x2,y2),其中x2﹣x1=1,若|y2﹣y1|<1,则x1的取值范围是 .
16.(2021秋 金安区期中)双曲线C1:y=和C2:y=如图所示,点A是C1上一点,分别过点A作AB⊥x轴,AC⊥y轴,垂足分别为点B、点C,AB,AC与C2分别交于点D、点E,若四边形ADOE的面积为4,则k1﹣k2= .
三.解答题
17.(2021 红桥区模拟)如图,它是反比例函数y=(m为常数,且m≠5)图象的一支.
(Ⅰ)图象的另一支位于哪个象限?求m的取值范围;
(Ⅱ)点A(2,3)在该反比例函数的图象上.
①判断点B(3,2),C(4,﹣2),D(﹣1,﹣6)是否在这个函数的图象上,并说明理由;
②在该函数图象的某一支上任取点M(x1,y1)和N(x2,y2).如果x1<x2,那么y1和y2有怎样的大小关系?
18.(2021秋 白云区期末)已知函数y=(k﹣2)xk+2为反比例函数.
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于第 象限;在每一个象限内,y随x的增大而 ;
(3)当﹣3≤x≤﹣时,函数的最大值为 ,最小值为 .
19.(2021秋 虹口区校级期末)已知函数y=y1﹣y2,且y1为x的反比例函数,y2为x的正比例函数,且和x=1时,y的值都是1.求y关于x的函数关系式.
20.(2021秋 覃塘区期中)已知点(﹣2,3)在反比例函数y=的图象上.
(1)求k的值;
(2)已知a>0且a≠1,A(a,y1)与B(a﹣1,y2)两点都在该反比例函数的图象上,试比较y1与y2的大小.
21.(2021 雷州市三模)如图,一次函数y=kx+b的图象与反比例函数y=﹣的图象交于A(﹣4,2),B(2,c)两点,一次函数与x轴交于点C,
(1)求一次函数的解析式和点C的坐标;
(2)连接AO、BO,求△AOB的面积;
(3)点P为x轴上的一点,连接BP,若S△BCP=2S△AOB,请求出点P的坐标.
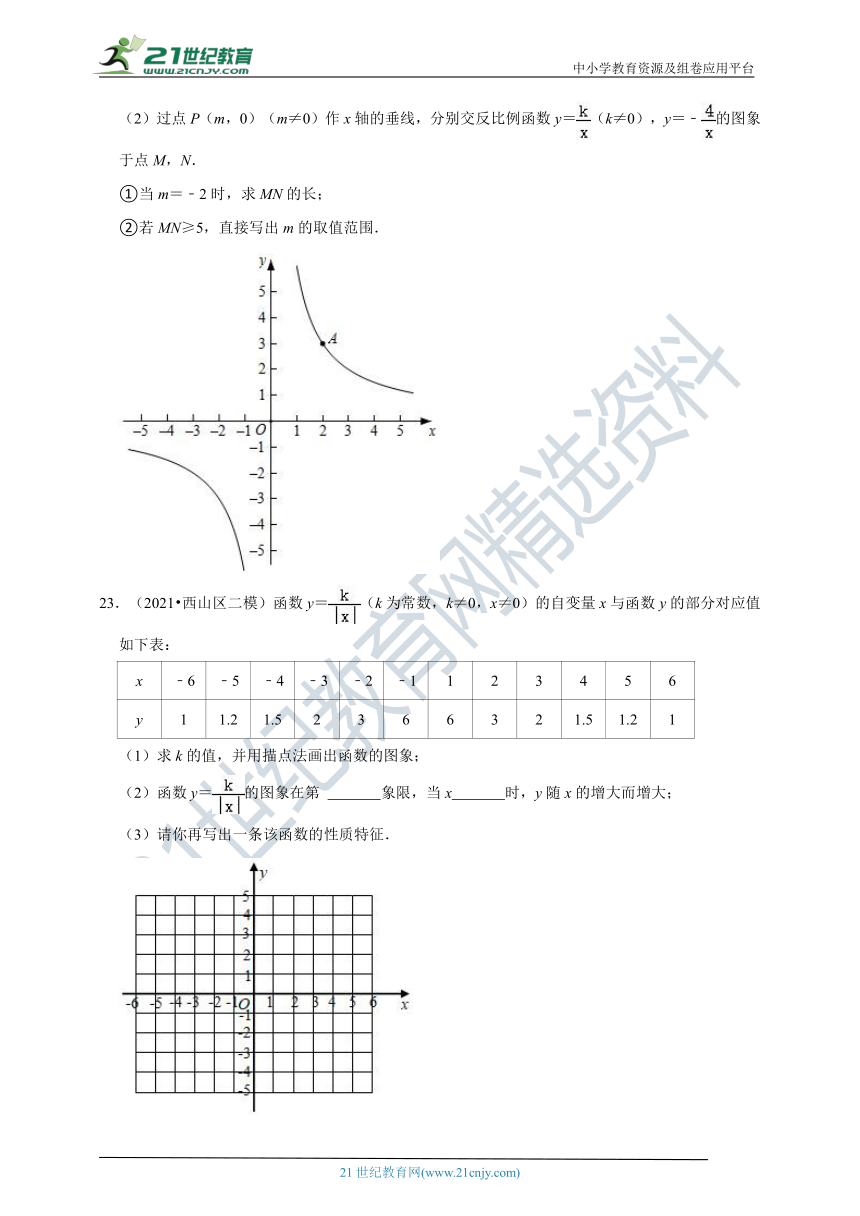
22.(2021秋 石景山区期末)在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象过点A(2,3).
(1)求k的值;
(2)过点P(m,0)(m≠0)作x轴的垂线,分别交反比例函数y=(k≠0),y=﹣的图象于点M,N.
①当m=﹣2时,求MN的长;
②若MN≥5,直接写出m的取值范围.
23.(2021 西山区二模)函数y=(k为常数,k≠0,x≠0)的自变量x与函数y的部分对应值如下表:
x ﹣6 ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y 1 1.2 1.5 2 3 6 6 3 2 1.5 1.2 1
(1)求k的值,并用描点法画出函数的图象;
(2)函数y=的图象在第 象限,当x 时,y随x的增大而增大;
(3)请你再写出一条该函数的性质特征.
答案与解析
一.选择题
1.(2021秋 揭西县期末)下列关系式中y是x的反比例函数的是( )
A.y=5x B. C. D.xy=3
【解析】解:A.y=5x,是正比例函数,故A不符合题意;
B.y=(k为常数,k≠0)是反比例函数,故B不符合题意;
C.y=,不是y是x的反比例函数,故C不符合题意;
D.xy=3,是反比例函数,故D符合题意;
故选:D.
2.(2021秋 徐汇区校级期末)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
【解析】解:A、y=是反比例函数,∵2>0,故在第一象限内y随x的增大而减小,不符合题意;
B、y=﹣2x是正比例函数,k=﹣2<0,故y随着x增大而减小,符合题意;
C、y=是反比例函数,∵﹣2<0,故在第一象限内y随x的增大而减小,不符合题意;
D、y=2x,正比例函数,k>0,故y随着x增大而增大,不符合题意;
故选:B.
3.(2021秋 南海区期末)已知反比例函数经过点A(3,2)、B(﹣1,m),则m的值为( )
A.﹣6 B. C. D.6
【解析】解:∵反比例函数经过点A(3,2),
∴k=3×2=6,
∴y=,
将点B(﹣1,m)代入反比例函数解析式得:
m=﹣6,
故选:A.
4.(2021秋 运城期末)点A(﹣3,y1),B(1,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y1>y3>y2 C.y2>y2>y1 D.y3>y1>y2
【解析】解:∵反比例函数y=中,k=﹣3<0,
∴此函数图象在二、四象限,
∵﹣3<0,
∴点A(﹣3,y1)在第二象限,
∴y1>0,
∵3>1>0,
∴B(1,y2),C(3,y3)两点在第四象限,
∴y2<y3<0.
∴y1,y2,y3的大小关系为y1>y3>y2.
故选:B.
5.(2021秋 徐汇区期末)如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,﹣4),那么另一个交点的坐标为( )
A.(﹣3,﹣4) B.(3,4) C.(﹣3,4) D.(﹣4,3)
【解析】解:由正比例函数图象和反比例函数图象的性质得,图象的两个交点是关于原点对称的,
∵正比例函数图象与反比例函数图象的一个交点的坐标为(3,﹣4),
∴另一个交点的坐标为(﹣3,4),
故选:C.
6.(2021秋 大同期末)已知点A(3,﹣4)在反比例函数y=的图象上,则下列说法正确的是( )
A.图象位于第一、三象限 B.点(2,6)在该函数图象上
C.当x<0时,y随x的增大而增大 D.当y≥﹣4时,x≥3
【解析】解:∵点A(3,﹣4)在反比例函数y=的图象上,
∴k=xy=3×(﹣4)=﹣12,
A、∵k=﹣12<0,
∴此函数的图象位于二、四象限,故本选项错误;
B、∵2×6=12≠﹣12,
∴点(2、6)不在此函数的图象上,故本选项错误;
C、∵k=﹣12<0,
∴在每一象限内y随x的增大而增大,
∴当x<0时,y随x的增大而增大,故本选项正确;
D、∵当y≥﹣4时,即﹣≥﹣4,
解得x<0或x≥3,故本选项错误;
故选:C.
7.(2021秋 市中区期末)如图,关于x的函数y=﹣(k≠0)和y=kx﹣k,它们在同一坐标系内的图象大致是( )
A.B. C. D.
【解析】解:A、由反比例函数图象可得k<0,∴一次函数y=kx﹣k应经过一二四象限,故A选项错误;
B、由反比例函数图象可得k>0,∴一次函数y=kx﹣k应经过一三四象限,故B选项正确;
C、由反比例函数图象可得k<0,∴一次函数y=kx﹣k应经过一二四象限,故C选项错误;
D、由反比例函数图象可得k>0,∴一次函数y=kx﹣k应经过一三四象限,故D选项错误;
故选:B.
8.(2021秋 金牛区期末)如图,一次函数y=kx+b(k≠0)图象与反比例函数y=(m≠0)图象交于点A(﹣1,2),B(2,﹣1),则不等式kx+b<的解集是( )
A.x<﹣1或x>2 B.﹣1<x<0或0<x<2 C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
【解析】解:由函数图象可知,当一次函数y=kx+b(k≠0)图象在反比例函数y=(m≠0)图象下方时,x的取值范围是:﹣1<x<0或x>2,
∴不等式kx+b<的解集是:﹣1<x<0或x>2,
故选:D.
9.(2021秋 鸡冠区校级期末)如图,已知反比例函数y=(x>0)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为3,则k的值为( )
A.6 B.12 C.﹣3 D.﹣6
【解析】解:设P的坐标是(m,n),则mn=k,
PA=n,△ABP中,AP边上的高是m,
∵△PAB的面积为3,即|mn|=3,
∴k=mn=﹣6.
故选:D.
10.(2021秋 和平区期末)如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△OAQ的面积为S2,若S1+S2=3,则k的值为( )
A.2 B.1 C.﹣1 D.﹣2
【解析】解:由题意得S1=|k|,,
则,
解得|k|=2,
∵图象在二、四象,
∴k<0,
∴k=﹣2.
故选:D.
二.填空题
11.(2021秋 鸡冠区校级期末)已知函数y=(m+2)x|m|﹣3是关于x的反比例函数,则实数m的值是 2 .
【解析】解:由题意得:
|m|﹣3=﹣1,且m+2≠0,
∴m=2,
故答案为:2.
12.(2021秋 正定县期末)已知反比例函数y=的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是 m>﹣ .
【解析】解:∵反比例函数y=的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,
∴1+3m>0,
解得,m>﹣,
故答案为m>﹣.
13.(2021秋 蓬江区期末)如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣2的图象交于点P(a,b),则代数式的值为 ﹣ .
【解析】解:∵函数y=(x>0)与y=x﹣2的图象交于点P(a,b),
∴ab=,b=a﹣2,
∴b﹣a=﹣2,
∴===﹣,
故答案为:﹣.
14.(2021秋 仙居县期末)已知反比例函数y=,若y>﹣1,则x的取值范围是 x<﹣3或x>0 .
【解析】解:∵y=,
∴该函数图象在第一、三象限,当x<0时,y<0;当x>0时,y>0;
∴当y>﹣1时,则>﹣1,x<0,
解得,x<﹣3或x>0,
故答案为:x<﹣3或x>0.
15.(2021秋 海淀区校级期末)对于函数y=图象上任意两点A(x1,y1),B(x2,y2),其中x2﹣x1=1,若|y2﹣y1|<1,则x1的取值范围是 x1>2或x1<﹣3 .
【解析】解:∵x2﹣x1=1,
∴x2=x1+1,
∴y1=,y2=,
∵|y2﹣y1|<1,
∴|﹣|<1,
∴||<1,
∴|x1(x1+1)|>6,
∴x1(x1+1)>6或x1(x1+1)<﹣6,
解得x1>2或x1<﹣3,
故答案为:x1>2或x1<﹣3.
16.(2021秋 金安区期中)双曲线C1:y=和C2:y=如图所示,点A是C1上一点,分别过点A作AB⊥x轴,AC⊥y轴,垂足分别为点B、点C,AB,AC与C2分别交于点D、点E,若四边形ADOE的面积为4,则k1﹣k2= ﹣4 .
【解析】解:∵D,E在反比例函数y=的图象上,且图象在第二象限,
∴S△OBD=OB BD=﹣k2,S△OCE=OC CE=﹣k2,
∵A在反比例函数y=的图象上,且图象在第二象限,
∴S矩形ABOC=OB OC=﹣k1
∴k1﹣k2=﹣[﹣k1﹣(﹣k2)]=﹣(S矩形ABOC﹣S△OBD﹣S△OCE)=﹣S四边形ADOE=﹣4,
故答案为:﹣4.
三.解答题
17.(2021 红桥区模拟)如图,它是反比例函数y=(m为常数,且m≠5)图象的一支.
(Ⅰ)图象的另一支位于哪个象限?求m的取值范围;
(Ⅱ)点A(2,3)在该反比例函数的图象上.
①判断点B(3,2),C(4,﹣2),D(﹣1,﹣6)是否在这个函数的图象上,并说明理由;
②在该函数图象的某一支上任取点M(x1,y1)和N(x2,y2).如果x1<x2,那么y1和y2有怎样的大小关系?
【解析】解:(Ⅰ)由图象在第一象限,根据对称性可知另一支位于第三象限,
∵图象在第一、三象限,
∴m﹣5>0,解得m>5;
(Ⅱ)∵点A(2,3)在该反比例函数的图象上,
∴m﹣5=2×3=6,
①点B(3,2)和D(﹣1,﹣6)在这个函数的图象上,
∵3×2=6,4×(﹣2)=﹣8≠6,﹣1×(﹣6)=6,
∴点B(3,2)和D(﹣1,﹣6)在这个函数的图象上,点C不在这个函数图象上;
②∵反比例函数图象在第一、三象限,
∴在每一个象限内y随x的增大而减小,
∵x1<x2,
∴y1>y2.
18.(2021秋 白云区期末)已知函数y=(k﹣2)xk+2为反比例函数.
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于第 二、四 象限;在每一个象限内,y随x的增大而 增大 ;
(3)当﹣3≤x≤﹣时,函数的最大值为 10 ,最小值为 .
【解析】解:(1)由题意得:k+2=﹣1,且k﹣2≠0,
解得:k=﹣3,
∴k﹣2=﹣5,
∴这个反比例函数的解析式为;
(2)∵﹣5<0,
∴图象在第二、四象限,在各象限内,y随x增大而增大;
故答案为:二、四;增大;
(3)当x=﹣3时,y最小==;
当x=﹣时,y最大==10;
故答案为:10;.
19.(2021秋 虹口区校级期末)已知函数y=y1﹣y2,且y1为x的反比例函数,y2为x的正比例函数,且和x=1时,y的值都是1.求y关于x的函数关系式.
【解析】解:∵y1与x成反比例,y2与x成正比例,
∴y1=,y2=kx.
∵y=y1﹣y2,
∴y=﹣kx,
∵当x=﹣时,y=1;当x=1时,y=1,
∴,
∴
∴y=﹣2x.
20.(2021秋 覃塘区期中)已知点(﹣2,3)在反比例函数y=的图象上.
(1)求k的值;
(2)已知a>0且a≠1,A(a,y1)与B(a﹣1,y2)两点都在该反比例函数的图象上,试比较y1与y2的大小.
【解析】解:(1)∵点(﹣2,3)在反比例函数y=的图象上,
∴k=﹣2×3=﹣6,
∴这个反比例函数的解析式为y=﹣;
(2)∵y=﹣中k=﹣6<0,
∴在每个象限函数值y随x的增大而增大,
当a>1,a﹣1>0时,A(a,y1)与B(a﹣1,y2)两点都在第四象限,
∴y1>y2;
当0<a<1,﹣1<a﹣1<0时,A(a,y1)在第四象限,B(a﹣1,y2)在第二象限,
∴y1<y2.
21.(2021 雷州市三模)如图,一次函数y=kx+b的图象与反比例函数y=﹣的图象交于A(﹣4,2),B(2,c)两点,一次函数与x轴交于点C,
(1)求一次函数的解析式和点C的坐标;
(2)连接AO、BO,求△AOB的面积;
(3)点P为x轴上的一点,连接BP,若S△BCP=2S△AOB,请求出点P的坐标.
【解析】解:(1)把B(2,c)代入,
∴,
∴B(2,﹣4),
把A(﹣4,2),B(2,﹣4)代入y=kx+b得,
∴,
所以一次函数为:y=﹣x﹣2.
令y=0,则﹣x﹣2=0,
∴x=﹣2,
∴C(﹣2,0);
(2)如图,连接OA,OB,
∴,
,
∴S△AOB=2+4=6.
(3)设P的坐标为(x,0),则PC=|x+2|,
由(2)得S△AOB=6,
∴S△BCP=2S△AOB=12,
∴,
∴x+2=±6,
∴x=4或﹣8,
∴P的坐标为(4,0)或(﹣8,0).
22.(2021秋 石景山区期末)在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象过点A(2,3).
(1)求k的值;
(2)过点P(m,0)(m≠0)作x轴的垂线,分别交反比例函数y=(k≠0),y=﹣的图象于点M,N.
①当m=﹣2时,求MN的长;
②若MN≥5,直接写出m的取值范围.
【解析】解:(1)∵反比例函数y=(k≠0)的图象过点A(2,3),
∴k=2×3=6;
(2)①当m=﹣2时,则P(﹣2,0),
把x=﹣2代入y=得,y=﹣3,
∴M(﹣2,﹣3),
把x=﹣2代入y=﹣得,y=2,
∴N(﹣2,2),
∴MN=2﹣(﹣3)=5;
②若MN≥5,m的取值范围是﹣2≤m<0或0<m≤2.
23.(2021 西山区二模)函数y=(k为常数,k≠0,x≠0)的自变量x与函数y的部分对应值如下表:
x ﹣6 ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y 1 1.2 1.5 2 3 6 6 3 2 1.5 1.2 1
(1)求k的值,并用描点法画出函数的图象;
(2)函数y=的图象在第 一、二 象限,当x <0 时,y随x的增大而增大;
(3)请你再写出一条该函数的性质特征.
【解析】解:(1)把x=3,y=2代入函数中得:k=6,
函数图象如图所示:
(2)根据图象可知:函数y=的图象在第一、二象限,当x<0时,y随x的增大而增大;
故答案为:一、二;x<0;
(3)再写一条该函数的性质特征为:函数图象关于y轴对称(合理即可).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下 26.1反比例函数同步练习
一.选择题
1.(2021秋 揭西县期末)下列关系式中y是x的反比例函数的是( )
A.y=5x B. C. D.xy=3
2.(2021秋 徐汇区校级期末)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
3.(2021秋 南海区期末)已知反比例函数经过点A(3,2)、B(﹣1,m),则m的值为( )
A.﹣6 B. C. D.6
4.(2021秋 运城期末)点A(﹣3,y1),B(1,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y1>y3>y2 C.y2>y2>y1 D.y3>y1>y2
5.(2021秋 徐汇区期末)如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,﹣4),那么另一个交点的坐标为( )
A.(﹣3,﹣4) B.(3,4) C.(﹣3,4) D.(﹣4,3)
6.(2021秋 大同期末)已知点A(3,﹣4)在反比例函数y=的图象上,则下列说法正确的是( )
A.图象位于第一、三象限 B.点(2,6)在该函数图象上
C.当x<0时,y随x的增大而增大 D.当y≥﹣4时,x≥3
7.(2021秋 市中区期末)如图,关于x的函数y=﹣(k≠0)和y=kx﹣k,它们在同一坐标系内的图象大致是( )
A.B. C. D.
8.(2021秋 金牛区期末)如图,一次函数y=kx+b(k≠0)图象与反比例函数y=(m≠0)图象交于点A(﹣1,2),B(2,﹣1),则不等式kx+b<的解集是( )
A.x<﹣1或x>2 B.﹣1<x<0或0<x<2 C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
9.(2021秋 鸡冠区校级期末)如图,已知反比例函数y=(x>0)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为3,则k的值为( )
A.6 B.12 C.﹣3 D.﹣6
10.(2021秋 和平区期末)如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△OAQ的面积为S2,若S1+S2=3,则k的值为( )
A.2 B.1 C.﹣1 D.﹣2
二.填空题
11.(2021秋 鸡冠区校级期末)已知函数y=(m+2)x|m|﹣3是关于x的反比例函数,则实数m的值是 .
12.(2021秋 正定县期末)已知反比例函数y=的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是 .
13.(2021秋 蓬江区期末)如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣2的图象交于点P(a,b),则代数式的值为 .
14.(2021秋 仙居县期末)已知反比例函数y=,若y>﹣1,则x的取值范围是 .
15.(2021秋 海淀区校级期末)对于函数y=图象上任意两点A(x1,y1),B(x2,y2),其中x2﹣x1=1,若|y2﹣y1|<1,则x1的取值范围是 .
16.(2021秋 金安区期中)双曲线C1:y=和C2:y=如图所示,点A是C1上一点,分别过点A作AB⊥x轴,AC⊥y轴,垂足分别为点B、点C,AB,AC与C2分别交于点D、点E,若四边形ADOE的面积为4,则k1﹣k2= .
三.解答题
17.(2021 红桥区模拟)如图,它是反比例函数y=(m为常数,且m≠5)图象的一支.
(Ⅰ)图象的另一支位于哪个象限?求m的取值范围;
(Ⅱ)点A(2,3)在该反比例函数的图象上.
①判断点B(3,2),C(4,﹣2),D(﹣1,﹣6)是否在这个函数的图象上,并说明理由;
②在该函数图象的某一支上任取点M(x1,y1)和N(x2,y2).如果x1<x2,那么y1和y2有怎样的大小关系?
18.(2021秋 白云区期末)已知函数y=(k﹣2)xk+2为反比例函数.
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于第 象限;在每一个象限内,y随x的增大而 ;
(3)当﹣3≤x≤﹣时,函数的最大值为 ,最小值为 .
19.(2021秋 虹口区校级期末)已知函数y=y1﹣y2,且y1为x的反比例函数,y2为x的正比例函数,且和x=1时,y的值都是1.求y关于x的函数关系式.
20.(2021秋 覃塘区期中)已知点(﹣2,3)在反比例函数y=的图象上.
(1)求k的值;
(2)已知a>0且a≠1,A(a,y1)与B(a﹣1,y2)两点都在该反比例函数的图象上,试比较y1与y2的大小.
21.(2021 雷州市三模)如图,一次函数y=kx+b的图象与反比例函数y=﹣的图象交于A(﹣4,2),B(2,c)两点,一次函数与x轴交于点C,
(1)求一次函数的解析式和点C的坐标;
(2)连接AO、BO,求△AOB的面积;
(3)点P为x轴上的一点,连接BP,若S△BCP=2S△AOB,请求出点P的坐标.
22.(2021秋 石景山区期末)在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象过点A(2,3).
(1)求k的值;
(2)过点P(m,0)(m≠0)作x轴的垂线,分别交反比例函数y=(k≠0),y=﹣的图象于点M,N.
①当m=﹣2时,求MN的长;
②若MN≥5,直接写出m的取值范围.
23.(2021 西山区二模)函数y=(k为常数,k≠0,x≠0)的自变量x与函数y的部分对应值如下表:
x ﹣6 ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y 1 1.2 1.5 2 3 6 6 3 2 1.5 1.2 1
(1)求k的值,并用描点法画出函数的图象;
(2)函数y=的图象在第 象限,当x 时,y随x的增大而增大;
(3)请你再写出一条该函数的性质特征.
答案与解析
一.选择题
1.(2021秋 揭西县期末)下列关系式中y是x的反比例函数的是( )
A.y=5x B. C. D.xy=3
【解析】解:A.y=5x,是正比例函数,故A不符合题意;
B.y=(k为常数,k≠0)是反比例函数,故B不符合题意;
C.y=,不是y是x的反比例函数,故C不符合题意;
D.xy=3,是反比例函数,故D符合题意;
故选:D.
2.(2021秋 徐汇区校级期末)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
【解析】解:A、y=是反比例函数,∵2>0,故在第一象限内y随x的增大而减小,不符合题意;
B、y=﹣2x是正比例函数,k=﹣2<0,故y随着x增大而减小,符合题意;
C、y=是反比例函数,∵﹣2<0,故在第一象限内y随x的增大而减小,不符合题意;
D、y=2x,正比例函数,k>0,故y随着x增大而增大,不符合题意;
故选:B.
3.(2021秋 南海区期末)已知反比例函数经过点A(3,2)、B(﹣1,m),则m的值为( )
A.﹣6 B. C. D.6
【解析】解:∵反比例函数经过点A(3,2),
∴k=3×2=6,
∴y=,
将点B(﹣1,m)代入反比例函数解析式得:
m=﹣6,
故选:A.
4.(2021秋 运城期末)点A(﹣3,y1),B(1,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y1>y3>y2 C.y2>y2>y1 D.y3>y1>y2
【解析】解:∵反比例函数y=中,k=﹣3<0,
∴此函数图象在二、四象限,
∵﹣3<0,
∴点A(﹣3,y1)在第二象限,
∴y1>0,
∵3>1>0,
∴B(1,y2),C(3,y3)两点在第四象限,
∴y2<y3<0.
∴y1,y2,y3的大小关系为y1>y3>y2.
故选:B.
5.(2021秋 徐汇区期末)如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,﹣4),那么另一个交点的坐标为( )
A.(﹣3,﹣4) B.(3,4) C.(﹣3,4) D.(﹣4,3)
【解析】解:由正比例函数图象和反比例函数图象的性质得,图象的两个交点是关于原点对称的,
∵正比例函数图象与反比例函数图象的一个交点的坐标为(3,﹣4),
∴另一个交点的坐标为(﹣3,4),
故选:C.
6.(2021秋 大同期末)已知点A(3,﹣4)在反比例函数y=的图象上,则下列说法正确的是( )
A.图象位于第一、三象限 B.点(2,6)在该函数图象上
C.当x<0时,y随x的增大而增大 D.当y≥﹣4时,x≥3
【解析】解:∵点A(3,﹣4)在反比例函数y=的图象上,
∴k=xy=3×(﹣4)=﹣12,
A、∵k=﹣12<0,
∴此函数的图象位于二、四象限,故本选项错误;
B、∵2×6=12≠﹣12,
∴点(2、6)不在此函数的图象上,故本选项错误;
C、∵k=﹣12<0,
∴在每一象限内y随x的增大而增大,
∴当x<0时,y随x的增大而增大,故本选项正确;
D、∵当y≥﹣4时,即﹣≥﹣4,
解得x<0或x≥3,故本选项错误;
故选:C.
7.(2021秋 市中区期末)如图,关于x的函数y=﹣(k≠0)和y=kx﹣k,它们在同一坐标系内的图象大致是( )
A.B. C. D.
【解析】解:A、由反比例函数图象可得k<0,∴一次函数y=kx﹣k应经过一二四象限,故A选项错误;
B、由反比例函数图象可得k>0,∴一次函数y=kx﹣k应经过一三四象限,故B选项正确;
C、由反比例函数图象可得k<0,∴一次函数y=kx﹣k应经过一二四象限,故C选项错误;
D、由反比例函数图象可得k>0,∴一次函数y=kx﹣k应经过一三四象限,故D选项错误;
故选:B.
8.(2021秋 金牛区期末)如图,一次函数y=kx+b(k≠0)图象与反比例函数y=(m≠0)图象交于点A(﹣1,2),B(2,﹣1),则不等式kx+b<的解集是( )
A.x<﹣1或x>2 B.﹣1<x<0或0<x<2 C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
【解析】解:由函数图象可知,当一次函数y=kx+b(k≠0)图象在反比例函数y=(m≠0)图象下方时,x的取值范围是:﹣1<x<0或x>2,
∴不等式kx+b<的解集是:﹣1<x<0或x>2,
故选:D.
9.(2021秋 鸡冠区校级期末)如图,已知反比例函数y=(x>0)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为3,则k的值为( )
A.6 B.12 C.﹣3 D.﹣6
【解析】解:设P的坐标是(m,n),则mn=k,
PA=n,△ABP中,AP边上的高是m,
∵△PAB的面积为3,即|mn|=3,
∴k=mn=﹣6.
故选:D.
10.(2021秋 和平区期末)如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△OAQ的面积为S2,若S1+S2=3,则k的值为( )
A.2 B.1 C.﹣1 D.﹣2
【解析】解:由题意得S1=|k|,,
则,
解得|k|=2,
∵图象在二、四象,
∴k<0,
∴k=﹣2.
故选:D.
二.填空题
11.(2021秋 鸡冠区校级期末)已知函数y=(m+2)x|m|﹣3是关于x的反比例函数,则实数m的值是 2 .
【解析】解:由题意得:
|m|﹣3=﹣1,且m+2≠0,
∴m=2,
故答案为:2.
12.(2021秋 正定县期末)已知反比例函数y=的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是 m>﹣ .
【解析】解:∵反比例函数y=的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,
∴1+3m>0,
解得,m>﹣,
故答案为m>﹣.
13.(2021秋 蓬江区期末)如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣2的图象交于点P(a,b),则代数式的值为 ﹣ .
【解析】解:∵函数y=(x>0)与y=x﹣2的图象交于点P(a,b),
∴ab=,b=a﹣2,
∴b﹣a=﹣2,
∴===﹣,
故答案为:﹣.
14.(2021秋 仙居县期末)已知反比例函数y=,若y>﹣1,则x的取值范围是 x<﹣3或x>0 .
【解析】解:∵y=,
∴该函数图象在第一、三象限,当x<0时,y<0;当x>0时,y>0;
∴当y>﹣1时,则>﹣1,x<0,
解得,x<﹣3或x>0,
故答案为:x<﹣3或x>0.
15.(2021秋 海淀区校级期末)对于函数y=图象上任意两点A(x1,y1),B(x2,y2),其中x2﹣x1=1,若|y2﹣y1|<1,则x1的取值范围是 x1>2或x1<﹣3 .
【解析】解:∵x2﹣x1=1,
∴x2=x1+1,
∴y1=,y2=,
∵|y2﹣y1|<1,
∴|﹣|<1,
∴||<1,
∴|x1(x1+1)|>6,
∴x1(x1+1)>6或x1(x1+1)<﹣6,
解得x1>2或x1<﹣3,
故答案为:x1>2或x1<﹣3.
16.(2021秋 金安区期中)双曲线C1:y=和C2:y=如图所示,点A是C1上一点,分别过点A作AB⊥x轴,AC⊥y轴,垂足分别为点B、点C,AB,AC与C2分别交于点D、点E,若四边形ADOE的面积为4,则k1﹣k2= ﹣4 .
【解析】解:∵D,E在反比例函数y=的图象上,且图象在第二象限,
∴S△OBD=OB BD=﹣k2,S△OCE=OC CE=﹣k2,
∵A在反比例函数y=的图象上,且图象在第二象限,
∴S矩形ABOC=OB OC=﹣k1
∴k1﹣k2=﹣[﹣k1﹣(﹣k2)]=﹣(S矩形ABOC﹣S△OBD﹣S△OCE)=﹣S四边形ADOE=﹣4,
故答案为:﹣4.
三.解答题
17.(2021 红桥区模拟)如图,它是反比例函数y=(m为常数,且m≠5)图象的一支.
(Ⅰ)图象的另一支位于哪个象限?求m的取值范围;
(Ⅱ)点A(2,3)在该反比例函数的图象上.
①判断点B(3,2),C(4,﹣2),D(﹣1,﹣6)是否在这个函数的图象上,并说明理由;
②在该函数图象的某一支上任取点M(x1,y1)和N(x2,y2).如果x1<x2,那么y1和y2有怎样的大小关系?
【解析】解:(Ⅰ)由图象在第一象限,根据对称性可知另一支位于第三象限,
∵图象在第一、三象限,
∴m﹣5>0,解得m>5;
(Ⅱ)∵点A(2,3)在该反比例函数的图象上,
∴m﹣5=2×3=6,
①点B(3,2)和D(﹣1,﹣6)在这个函数的图象上,
∵3×2=6,4×(﹣2)=﹣8≠6,﹣1×(﹣6)=6,
∴点B(3,2)和D(﹣1,﹣6)在这个函数的图象上,点C不在这个函数图象上;
②∵反比例函数图象在第一、三象限,
∴在每一个象限内y随x的增大而减小,
∵x1<x2,
∴y1>y2.
18.(2021秋 白云区期末)已知函数y=(k﹣2)xk+2为反比例函数.
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于第 二、四 象限;在每一个象限内,y随x的增大而 增大 ;
(3)当﹣3≤x≤﹣时,函数的最大值为 10 ,最小值为 .
【解析】解:(1)由题意得:k+2=﹣1,且k﹣2≠0,
解得:k=﹣3,
∴k﹣2=﹣5,
∴这个反比例函数的解析式为;
(2)∵﹣5<0,
∴图象在第二、四象限,在各象限内,y随x增大而增大;
故答案为:二、四;增大;
(3)当x=﹣3时,y最小==;
当x=﹣时,y最大==10;
故答案为:10;.
19.(2021秋 虹口区校级期末)已知函数y=y1﹣y2,且y1为x的反比例函数,y2为x的正比例函数,且和x=1时,y的值都是1.求y关于x的函数关系式.
【解析】解:∵y1与x成反比例,y2与x成正比例,
∴y1=,y2=kx.
∵y=y1﹣y2,
∴y=﹣kx,
∵当x=﹣时,y=1;当x=1时,y=1,
∴,
∴
∴y=﹣2x.
20.(2021秋 覃塘区期中)已知点(﹣2,3)在反比例函数y=的图象上.
(1)求k的值;
(2)已知a>0且a≠1,A(a,y1)与B(a﹣1,y2)两点都在该反比例函数的图象上,试比较y1与y2的大小.
【解析】解:(1)∵点(﹣2,3)在反比例函数y=的图象上,
∴k=﹣2×3=﹣6,
∴这个反比例函数的解析式为y=﹣;
(2)∵y=﹣中k=﹣6<0,
∴在每个象限函数值y随x的增大而增大,
当a>1,a﹣1>0时,A(a,y1)与B(a﹣1,y2)两点都在第四象限,
∴y1>y2;
当0<a<1,﹣1<a﹣1<0时,A(a,y1)在第四象限,B(a﹣1,y2)在第二象限,
∴y1<y2.
21.(2021 雷州市三模)如图,一次函数y=kx+b的图象与反比例函数y=﹣的图象交于A(﹣4,2),B(2,c)两点,一次函数与x轴交于点C,
(1)求一次函数的解析式和点C的坐标;
(2)连接AO、BO,求△AOB的面积;
(3)点P为x轴上的一点,连接BP,若S△BCP=2S△AOB,请求出点P的坐标.
【解析】解:(1)把B(2,c)代入,
∴,
∴B(2,﹣4),
把A(﹣4,2),B(2,﹣4)代入y=kx+b得,
∴,
所以一次函数为:y=﹣x﹣2.
令y=0,则﹣x﹣2=0,
∴x=﹣2,
∴C(﹣2,0);
(2)如图,连接OA,OB,
∴,
,
∴S△AOB=2+4=6.
(3)设P的坐标为(x,0),则PC=|x+2|,
由(2)得S△AOB=6,
∴S△BCP=2S△AOB=12,
∴,
∴x+2=±6,
∴x=4或﹣8,
∴P的坐标为(4,0)或(﹣8,0).
22.(2021秋 石景山区期末)在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象过点A(2,3).
(1)求k的值;
(2)过点P(m,0)(m≠0)作x轴的垂线,分别交反比例函数y=(k≠0),y=﹣的图象于点M,N.
①当m=﹣2时,求MN的长;
②若MN≥5,直接写出m的取值范围.
【解析】解:(1)∵反比例函数y=(k≠0)的图象过点A(2,3),
∴k=2×3=6;
(2)①当m=﹣2时,则P(﹣2,0),
把x=﹣2代入y=得,y=﹣3,
∴M(﹣2,﹣3),
把x=﹣2代入y=﹣得,y=2,
∴N(﹣2,2),
∴MN=2﹣(﹣3)=5;
②若MN≥5,m的取值范围是﹣2≤m<0或0<m≤2.
23.(2021 西山区二模)函数y=(k为常数,k≠0,x≠0)的自变量x与函数y的部分对应值如下表:
x ﹣6 ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y 1 1.2 1.5 2 3 6 6 3 2 1.5 1.2 1
(1)求k的值,并用描点法画出函数的图象;
(2)函数y=的图象在第 一、二 象限,当x <0 时,y随x的增大而增大;
(3)请你再写出一条该函数的性质特征.
【解析】解:(1)把x=3,y=2代入函数中得:k=6,
函数图象如图所示:
(2)根据图象可知:函数y=的图象在第一、二象限,当x<0时,y随x的增大而增大;
故答案为:一、二;x<0;
(3)再写一条该函数的性质特征为:函数图象关于y轴对称(合理即可).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
