26.2 实际问题与反比例函数 同步练习(含解析)
文档属性
| 名称 | 26.2 实际问题与反比例函数 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 21:22:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级下 26.2实际问题与反比例函数同步练习
一.选择题
1.(2021秋 泰山区期中)如果等腰三角形的面积为6,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
2.(2020 莫旗一模)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
3.(2021 石景山区一模)下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
4.(2021春 海淀区校级月考)某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
5.(2021 云岩区模拟)阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
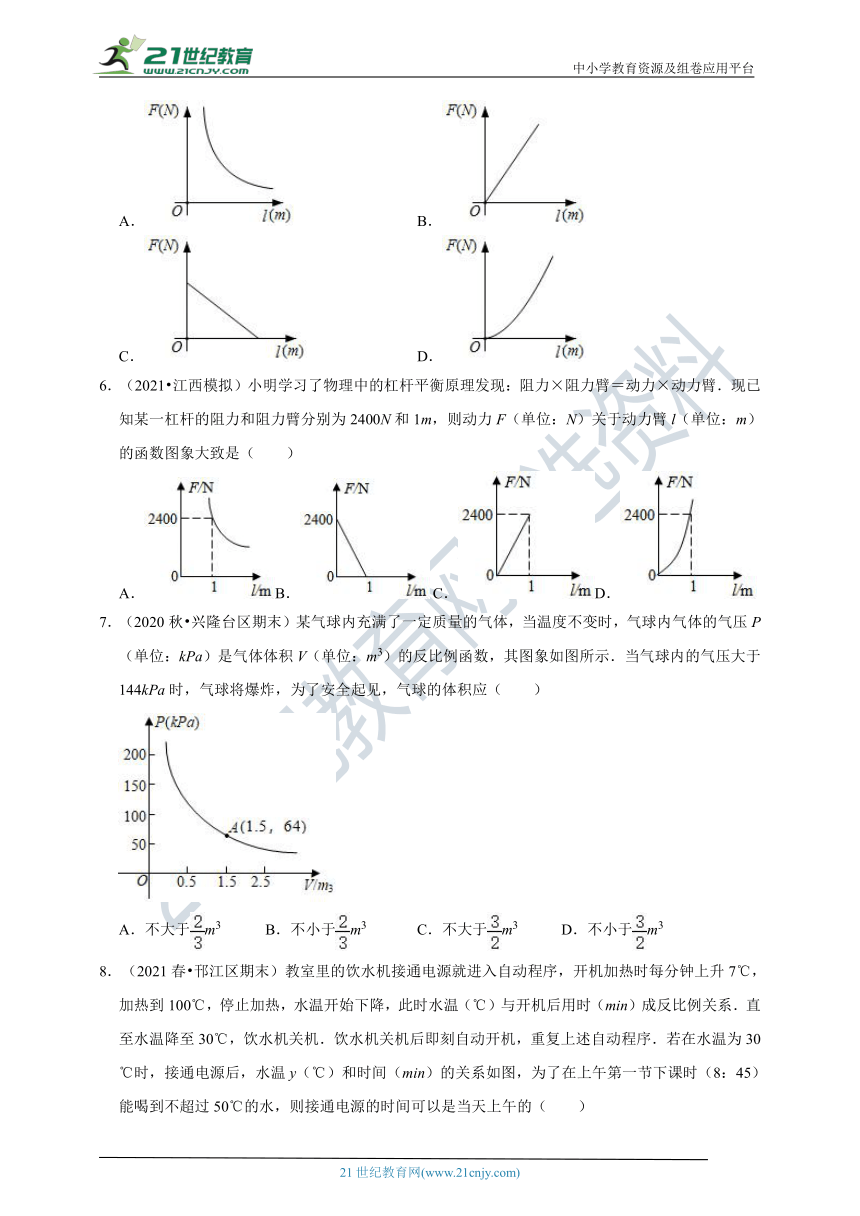
6.(2021 江西模拟)小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A.B. C.D.
7.(2020秋 兴隆台区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示.当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
8.(2021春 邗江区期末)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升7℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.8:00
二.填空题
9.(2020秋 斗门区期末)一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=10m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为 kg/m3.
10.(2021秋 和平区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气体体积为2m3时,气压是 kPa.
11.(2020秋 如皋市期中)调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
12.(2020秋 樊城区期末)某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积V的范围是 .
13.(2016 石景山区二模)为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过 分钟后教室内的空气才能达到安全要求.
14.(2013 聊城模拟)我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为200Ω的滑动变阻器及一电流表测电源电压,结果如图所示.
(1)电流I(安培)与电阻R(欧姆)之间的函数解析式为 ;
(2)当电阻在2Ω~200Ω之间时,电流应在 范围内,电流随电阻的增大而 ;
(3)若限制电流不超过20安培,则电阻在 之间.
三.解答题
15.(2021秋 永定区期中)在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.
(1)y关于x的函数关系式是 ,x的取值范围是 ;
(2)在平面直角坐标系中画出该函数图象.
16.(2021 吴兴区一模)已知一辆货车上装有20吨货物,货车到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)若要求不超过4小时卸完车上的这批货物,那么平均每小时至少要卸货多少吨?
17.(2021秋 仙居县期末)如图,取一根长1米的质地均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点30cm处挂一个重9.8牛的物体,在中点O右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧秤与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛,精确到0.1牛)有什么变化.小慧在做此《数学活动》时,得到下表的数据:
L/cm 5 10 15 20 25 30 35 40
F/牛 58.8 60.2 19.6 14.7 11.8 9.8 8.4 7.4
结果老师发现其中有一个数据明显有错误.
(1)你认为当L= cm时所对应的F数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出F与L的函数关系式;
(3)若弹簧秤的最大量程是60牛,求L的取值范围.
18.(2021 东胜区一模)A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
19.(2021秋 海淀区校级期末)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的函数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.
(1)写出该材料温度上升和下降阶段,y与x的函数关系式:
①上升阶段:当0≤x≤5时,y= ;
②下降阶段:当x>5时,y .
(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?
20.(2020秋 清涧县期末)李叔叔驾驶小汽车从A地匀速行驶到B地,行驶里程为480km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定不超过120km/h.
(1)求v与t之间的关系式;
(2)李叔叔上午8点驾驶小汽车从A地出发,需要在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
21.(2020秋 如皋市期末)为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
答案与解析
一.选择题
1.(2021秋 泰山区期中)如果等腰三角形的面积为6,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
【解析】解:∵等腰三角形的面积为6,底边长为x,底边上的高为y,
∴xy=6,
∴y与x的函数关系式为:y=.
故选:A.
2.(2020 莫旗一模)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
【解析】解:由于以80千米/时的平均速度用了6小时到达目的地,那么路程为80×6=480千米,
∴汽车的速度v(千米/时)与时间t(小时)的函数关系为v=.
故选:A.
3.(2021 石景山区一模)下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
【解析】解:A.圆的周长与其半径是正比例函数,故不符合题意;
B.平行四边形面积一定时,其一边长与这边上的高是反比例函数,故符合题意;
C.销售单价一定时,销售总价与销售数量是正比例函数,故不符合题意;
D.汽车匀速行驶过程中,行驶路程与行驶时间是正比例函数,故不符合题意.
故选:B.
4.(2021春 海淀区校级月考)某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
【解析】解:观察图象易知p与S之间的是反比例函数关系,设p=,
由于A(20,10)在此函数的图象上,
∴k=20×10=200,
∴p=.
故选:B.
5.(2021 云岩区模拟)阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
【解析】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=,是反比例函数,A选项符合,
故选:A.
6.(2021 江西模拟)小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A.B. C. D.
【解析】】解:∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是2400N和1m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:2400×1=Fl,
则F=,是反比例函数,A选项符合,
故选:A.
7.(2020秋 兴隆台区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示.当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
【解析】解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=
∵图象过点(1.5,64)
∴k=96,
即P=在第一象限内,P随V的增大而减小,
∴当P≤144时,V≥=.
故选:B.
8.(2021春 邗江区期末)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升7℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.8:00
【解析】解:∵开机加热时每分钟上升7℃,
∴加热到100℃所需要的时间为:=10min,
∴每次加热10min后,饮水机就会断电,开始冷却
设10分钟后,水温与开机所用时间所成的反比例函数为y=,
∵点(10,100)在反比例函数图象上,
∴k=1000,
∴反比例函数为,
令y=30,则,
∴,
∴每次开机加热min后,饮水机就要重新从30℃开始加热,
如果7:20开机至8:45,经过的时间为85分钟,
85﹣=>10,
∴此时饮水机第三次加热,从30℃加热了分钟,
水温为y==>50℃,
故A选项不合题意,
如果7:30开机至8:45,经过的时间为75分钟,
75﹣×2=<10,
∴此时饮水机第三次加热了,从30℃加热了分钟,
水温为30+=>50℃,
故B选项不合题意,
如果7:45开机至8:45,经过的时间为60分钟,
∴此时饮水机第二次加热,从30℃加热了20分钟,
水温为y==50,
故C选项符合题意,
如果8:00开机至8:45,经过的时间为45分钟,
∴此时饮水机第二次加热,从30℃加热了5分钟,
水温为y=30+5×7=65>50℃,
故D选项不符合题意,
故选:C.
二.填空题
9.(2020秋 斗门区期末)一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=10m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为 7 kg/m3.
【解析】解:设ρ=,
当V=10m3时,ρ=1.4kg/m3,
∴1.4=,
∴k=1.4×10=14,
∴ρ与V的函数关系式是ρ=;
当V=2m3时,ρ==7(kg/m3).
故答案为:7.
10.(2021秋 和平区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气体体积为2m3时,气压是 50 kPa.
【解析】解:设P=,
由图象知100=,
所以k=100,
故P=,
当V=2时,P==50;
故答案为:50.
11.(2020秋 如皋市期中)调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 300 元.
【解析】解:由表中数据得:xy=6000,
∴y=,
则所求函数关系式为y=;
由题意得:(x﹣180)y=2400,
把y=代入得:(x﹣180) =2400,
解得:x=300,
经检验,x=300是原方程的根,
答:要使该款运动鞋每天的销售利润达到2400元,则其售价应定为300元.
故答案为:300.
12.(2020秋 樊城区期末)某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积V的范围是 V≥ .
【解析】解:设气球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=,
∵图象过点(1.5,64),
∴k=96,
即P=,在第一象限内,P随V的增大而减小,
∴当P≤160时,V=≥.
故答案为:V≥.
13.(2016 石景山区二模)为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过 50 分钟后教室内的空气才能达到安全要求.
【解析】解:设药物燃烧后y与x之间的解析式y=,把点(10,8)代入y=得8=,
解得k2=80,
∴y关于x的函数式为:y=;
当y=1.6时,由y=;得x=50(11分),
所以50分钟后学生才可进入教室.
故答案为:50.
14.(2013 聊城模拟)我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为200Ω的滑动变阻器及一电流表测电源电压,结果如图所示.
(1)电流I(安培)与电阻R(欧姆)之间的函数解析式为 I= ;
(2)当电阻在2Ω~200Ω之间时,电流应在 0.72安培~72安培 范围内,电流随电阻的增大而 减小 ;
(3)若限制电流不超过20安培,则电阻在 7.2Ω~200Ω 之间.
【解析】解:(1)设函数解析式为I=,
将点A(8,18)代入,得m=144,
故函数解析式为I=;
(2)当2≤R≤200时,可得0.72≤I≤72,
故电流应在0.72安培~72安培范围内;电流随电阻的增大而减小;
(3)若限制电流不超过20安培,
则R≥=7.2(Ω),
∵最大电阻为200Ω的滑动变阻器,
∴电阻在7.2Ω~200Ω之间.
故答案为:(1)I=;(2)0.72安培~72安培,减小;(3)7.2Ω~200Ω.
三.解答题
15.(2021秋 永定区期中)在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.
(1)y关于x的函数关系式是 y= ,x的取值范围是 x>0 ;
(2)在平面直角坐标系中画出该函数图象.
【解析】解:(1)在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2,
∴xy=2,
∴xy=4,
∴y关于x的函数关系式是y=,
x的取值范围为x>0,
故答案为:y=,x>0;
(2)在平面直角坐标系中画出该函数图象如图所示.
16.(2021 吴兴区一模)已知一辆货车上装有20吨货物,货车到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)若要求不超过4小时卸完车上的这批货物,那么平均每小时至少要卸货多少吨?
【解析】解:(1)依题意得:vt=20,
∴v=(t>0).
(2)∵k=20>0,
∴在第一象限,v随t的增大而减小.
又当t=4时,v==5,
∴当0<t≤4时,v≥5.
答:平均每小时至少要卸货5吨.
17.(2021秋 仙居县期末)如图,取一根长1米的质地均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点30cm处挂一个重9.8牛的物体,在中点O右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧秤与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛,精确到0.1牛)有什么变化.小慧在做此《数学活动》时,得到下表的数据:
L/cm 5 10 15 20 25 30 35 40
F/牛 58.8 60.2 19.6 14.7 11.8 9.8 8.4 7.4
结果老师发现其中有一个数据明显有错误.
(1)你认为当L= 10 cm时所对应的F数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出F与L的函数关系式;
(3)若弹簧秤的最大量程是60牛,求L的取值范围.
【解析】解:(1)根据杠杆原理知 F L=30×9.8.
当L=10cm时,F=29.4牛顿.所以表格中数据错了;
(2)根据杠杆原理知F L=30×9.8.
∴F与L的函数关系式为:;
(3)当F=60牛时,由得L=4.9,
根据反比例函数的图像与性质可得L≥4.9,
∵由题意可知L≤50,
∴L的取值范围是4.9cm≤L≤50cm.
18.(2021 东胜区一模)A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
【解析】解:(1)根据题意,路程为400,
设小汽车的行驶时间为t小时,行驶速度为v千米/小时,
则v关于t的函数表达式为v=;
(2)设从A地匀速行驶到B地要t小时,则≤80,
解得:t≥5,
∴他从A地匀速行驶到B地至少要5小时;
(3)∵v≤100,
≤100,
解得:t≥4,
∴某人从A地出发最少用4个小时才能到达B地,
7点至10点40分,是3小时,
∴他不能在10点40分之前到达B地.
19.(2021秋 海淀区校级期末)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的函数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.
(1)写出该材料温度上升和下降阶段,y与x的函数关系式:
①上升阶段:当0≤x≤5时,y= 9x+15 ;
②下降阶段:当x>5时,y = .
(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?
【解析】解:(1)①上升阶段:当0≤x<5时,为一次函数,设一次函数表达式为y=kx+b,
由于一次函数图象过点(0,15),(5,60),
所以,
解得:,
所以y=9x+15,
②下降阶段:当x≥5时,为反比例函数,设函数关系式为:y=,
由于图象过点(5,60),所以m=300.
则y=;
故答案为:9x+15;=
(2)当0≤x<5时,y=9x+15=30,得x=,
因为y随x的增大而增大,所以x>,
当x≥5时,y==30,
得x=10,因为y随x的增大而减小,
所以x<10,
10﹣=,
答:可加工min.
20.(2020秋 清涧县期末)李叔叔驾驶小汽车从A地匀速行驶到B地,行驶里程为480km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定不超过120km/h.
(1)求v与t之间的关系式;
(2)李叔叔上午8点驾驶小汽车从A地出发,需要在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
【解析】解:(1)vt=480,且全程速度限定不超过120km/h,
∴v与t之间的关系式为.
(2)∵8点至12点4(8分)的时间长为4.8h,8点至14点的时间长为6h,
∴将t=6代入中,得v=80,
将t=4.8代入中,得v=100.
∴小汽车行驶速度v的范围为80≤v≤100.
21.(2020秋 如皋市期末)为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
【解析】解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1=,
设药物燃烧后y关于x的函数关系式为y=(k2>0),
代入(8,6)得6=,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:(x>8),
∴;
(2)有效,理由如下:
把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
∴这次消毒是有效的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下 26.2实际问题与反比例函数同步练习
一.选择题
1.(2021秋 泰山区期中)如果等腰三角形的面积为6,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
2.(2020 莫旗一模)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
3.(2021 石景山区一模)下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
4.(2021春 海淀区校级月考)某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
5.(2021 云岩区模拟)阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
6.(2021 江西模拟)小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A.B. C.D.
7.(2020秋 兴隆台区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示.当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
8.(2021春 邗江区期末)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升7℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.8:00
二.填空题
9.(2020秋 斗门区期末)一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=10m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为 kg/m3.
10.(2021秋 和平区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气体体积为2m3时,气压是 kPa.
11.(2020秋 如皋市期中)调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
12.(2020秋 樊城区期末)某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积V的范围是 .
13.(2016 石景山区二模)为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过 分钟后教室内的空气才能达到安全要求.
14.(2013 聊城模拟)我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为200Ω的滑动变阻器及一电流表测电源电压,结果如图所示.
(1)电流I(安培)与电阻R(欧姆)之间的函数解析式为 ;
(2)当电阻在2Ω~200Ω之间时,电流应在 范围内,电流随电阻的增大而 ;
(3)若限制电流不超过20安培,则电阻在 之间.
三.解答题
15.(2021秋 永定区期中)在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.
(1)y关于x的函数关系式是 ,x的取值范围是 ;
(2)在平面直角坐标系中画出该函数图象.
16.(2021 吴兴区一模)已知一辆货车上装有20吨货物,货车到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)若要求不超过4小时卸完车上的这批货物,那么平均每小时至少要卸货多少吨?
17.(2021秋 仙居县期末)如图,取一根长1米的质地均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点30cm处挂一个重9.8牛的物体,在中点O右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧秤与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛,精确到0.1牛)有什么变化.小慧在做此《数学活动》时,得到下表的数据:
L/cm 5 10 15 20 25 30 35 40
F/牛 58.8 60.2 19.6 14.7 11.8 9.8 8.4 7.4
结果老师发现其中有一个数据明显有错误.
(1)你认为当L= cm时所对应的F数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出F与L的函数关系式;
(3)若弹簧秤的最大量程是60牛,求L的取值范围.
18.(2021 东胜区一模)A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
19.(2021秋 海淀区校级期末)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的函数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.
(1)写出该材料温度上升和下降阶段,y与x的函数关系式:
①上升阶段:当0≤x≤5时,y= ;
②下降阶段:当x>5时,y .
(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?
20.(2020秋 清涧县期末)李叔叔驾驶小汽车从A地匀速行驶到B地,行驶里程为480km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定不超过120km/h.
(1)求v与t之间的关系式;
(2)李叔叔上午8点驾驶小汽车从A地出发,需要在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
21.(2020秋 如皋市期末)为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
答案与解析
一.选择题
1.(2021秋 泰山区期中)如果等腰三角形的面积为6,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
【解析】解:∵等腰三角形的面积为6,底边长为x,底边上的高为y,
∴xy=6,
∴y与x的函数关系式为:y=.
故选:A.
2.(2020 莫旗一模)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
【解析】解:由于以80千米/时的平均速度用了6小时到达目的地,那么路程为80×6=480千米,
∴汽车的速度v(千米/时)与时间t(小时)的函数关系为v=.
故选:A.
3.(2021 石景山区一模)下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
【解析】解:A.圆的周长与其半径是正比例函数,故不符合题意;
B.平行四边形面积一定时,其一边长与这边上的高是反比例函数,故符合题意;
C.销售单价一定时,销售总价与销售数量是正比例函数,故不符合题意;
D.汽车匀速行驶过程中,行驶路程与行驶时间是正比例函数,故不符合题意.
故选:B.
4.(2021春 海淀区校级月考)某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
【解析】解:观察图象易知p与S之间的是反比例函数关系,设p=,
由于A(20,10)在此函数的图象上,
∴k=20×10=200,
∴p=.
故选:B.
5.(2021 云岩区模拟)阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
【解析】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=,是反比例函数,A选项符合,
故选:A.
6.(2021 江西模拟)小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A.B. C. D.
【解析】】解:∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是2400N和1m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:2400×1=Fl,
则F=,是反比例函数,A选项符合,
故选:A.
7.(2020秋 兴隆台区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示.当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
【解析】解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=
∵图象过点(1.5,64)
∴k=96,
即P=在第一象限内,P随V的增大而减小,
∴当P≤144时,V≥=.
故选:B.
8.(2021春 邗江区期末)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升7℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.8:00
【解析】解:∵开机加热时每分钟上升7℃,
∴加热到100℃所需要的时间为:=10min,
∴每次加热10min后,饮水机就会断电,开始冷却
设10分钟后,水温与开机所用时间所成的反比例函数为y=,
∵点(10,100)在反比例函数图象上,
∴k=1000,
∴反比例函数为,
令y=30,则,
∴,
∴每次开机加热min后,饮水机就要重新从30℃开始加热,
如果7:20开机至8:45,经过的时间为85分钟,
85﹣=>10,
∴此时饮水机第三次加热,从30℃加热了分钟,
水温为y==>50℃,
故A选项不合题意,
如果7:30开机至8:45,经过的时间为75分钟,
75﹣×2=<10,
∴此时饮水机第三次加热了,从30℃加热了分钟,
水温为30+=>50℃,
故B选项不合题意,
如果7:45开机至8:45,经过的时间为60分钟,
∴此时饮水机第二次加热,从30℃加热了20分钟,
水温为y==50,
故C选项符合题意,
如果8:00开机至8:45,经过的时间为45分钟,
∴此时饮水机第二次加热,从30℃加热了5分钟,
水温为y=30+5×7=65>50℃,
故D选项不符合题意,
故选:C.
二.填空题
9.(2020秋 斗门区期末)一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=10m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为 7 kg/m3.
【解析】解:设ρ=,
当V=10m3时,ρ=1.4kg/m3,
∴1.4=,
∴k=1.4×10=14,
∴ρ与V的函数关系式是ρ=;
当V=2m3时,ρ==7(kg/m3).
故答案为:7.
10.(2021秋 和平区期末)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气体体积为2m3时,气压是 50 kPa.
【解析】解:设P=,
由图象知100=,
所以k=100,
故P=,
当V=2时,P==50;
故答案为:50.
11.(2020秋 如皋市期中)调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 300 元.
【解析】解:由表中数据得:xy=6000,
∴y=,
则所求函数关系式为y=;
由题意得:(x﹣180)y=2400,
把y=代入得:(x﹣180) =2400,
解得:x=300,
经检验,x=300是原方程的根,
答:要使该款运动鞋每天的销售利润达到2400元,则其售价应定为300元.
故答案为:300.
12.(2020秋 樊城区期末)某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积V的范围是 V≥ .
【解析】解:设气球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=,
∵图象过点(1.5,64),
∴k=96,
即P=,在第一象限内,P随V的增大而减小,
∴当P≤160时,V=≥.
故答案为:V≥.
13.(2016 石景山区二模)为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过 50 分钟后教室内的空气才能达到安全要求.
【解析】解:设药物燃烧后y与x之间的解析式y=,把点(10,8)代入y=得8=,
解得k2=80,
∴y关于x的函数式为:y=;
当y=1.6时,由y=;得x=50(11分),
所以50分钟后学生才可进入教室.
故答案为:50.
14.(2013 聊城模拟)我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为200Ω的滑动变阻器及一电流表测电源电压,结果如图所示.
(1)电流I(安培)与电阻R(欧姆)之间的函数解析式为 I= ;
(2)当电阻在2Ω~200Ω之间时,电流应在 0.72安培~72安培 范围内,电流随电阻的增大而 减小 ;
(3)若限制电流不超过20安培,则电阻在 7.2Ω~200Ω 之间.
【解析】解:(1)设函数解析式为I=,
将点A(8,18)代入,得m=144,
故函数解析式为I=;
(2)当2≤R≤200时,可得0.72≤I≤72,
故电流应在0.72安培~72安培范围内;电流随电阻的增大而减小;
(3)若限制电流不超过20安培,
则R≥=7.2(Ω),
∵最大电阻为200Ω的滑动变阻器,
∴电阻在7.2Ω~200Ω之间.
故答案为:(1)I=;(2)0.72安培~72安培,减小;(3)7.2Ω~200Ω.
三.解答题
15.(2021秋 永定区期中)在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2.
(1)y关于x的函数关系式是 y= ,x的取值范围是 x>0 ;
(2)在平面直角坐标系中画出该函数图象.
【解析】解:(1)在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为2,
∴xy=2,
∴xy=4,
∴y关于x的函数关系式是y=,
x的取值范围为x>0,
故答案为:y=,x>0;
(2)在平面直角坐标系中画出该函数图象如图所示.
16.(2021 吴兴区一模)已知一辆货车上装有20吨货物,货车到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)若要求不超过4小时卸完车上的这批货物,那么平均每小时至少要卸货多少吨?
【解析】解:(1)依题意得:vt=20,
∴v=(t>0).
(2)∵k=20>0,
∴在第一象限,v随t的增大而减小.
又当t=4时,v==5,
∴当0<t≤4时,v≥5.
答:平均每小时至少要卸货5吨.
17.(2021秋 仙居县期末)如图,取一根长1米的质地均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点30cm处挂一个重9.8牛的物体,在中点O右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧秤与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛,精确到0.1牛)有什么变化.小慧在做此《数学活动》时,得到下表的数据:
L/cm 5 10 15 20 25 30 35 40
F/牛 58.8 60.2 19.6 14.7 11.8 9.8 8.4 7.4
结果老师发现其中有一个数据明显有错误.
(1)你认为当L= 10 cm时所对应的F数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出F与L的函数关系式;
(3)若弹簧秤的最大量程是60牛,求L的取值范围.
【解析】解:(1)根据杠杆原理知 F L=30×9.8.
当L=10cm时,F=29.4牛顿.所以表格中数据错了;
(2)根据杠杆原理知F L=30×9.8.
∴F与L的函数关系式为:;
(3)当F=60牛时,由得L=4.9,
根据反比例函数的图像与性质可得L≥4.9,
∵由题意可知L≤50,
∴L的取值范围是4.9cm≤L≤50cm.
18.(2021 东胜区一模)A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
【解析】解:(1)根据题意,路程为400,
设小汽车的行驶时间为t小时,行驶速度为v千米/小时,
则v关于t的函数表达式为v=;
(2)设从A地匀速行驶到B地要t小时,则≤80,
解得:t≥5,
∴他从A地匀速行驶到B地至少要5小时;
(3)∵v≤100,
≤100,
解得:t≥4,
∴某人从A地出发最少用4个小时才能到达B地,
7点至10点40分,是3小时,
∴他不能在10点40分之前到达B地.
19.(2021秋 海淀区校级期末)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的函数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.
(1)写出该材料温度上升和下降阶段,y与x的函数关系式:
①上升阶段:当0≤x≤5时,y= 9x+15 ;
②下降阶段:当x>5时,y = .
(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?
【解析】解:(1)①上升阶段:当0≤x<5时,为一次函数,设一次函数表达式为y=kx+b,
由于一次函数图象过点(0,15),(5,60),
所以,
解得:,
所以y=9x+15,
②下降阶段:当x≥5时,为反比例函数,设函数关系式为:y=,
由于图象过点(5,60),所以m=300.
则y=;
故答案为:9x+15;=
(2)当0≤x<5时,y=9x+15=30,得x=,
因为y随x的增大而增大,所以x>,
当x≥5时,y==30,
得x=10,因为y随x的增大而减小,
所以x<10,
10﹣=,
答:可加工min.
20.(2020秋 清涧县期末)李叔叔驾驶小汽车从A地匀速行驶到B地,行驶里程为480km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定不超过120km/h.
(1)求v与t之间的关系式;
(2)李叔叔上午8点驾驶小汽车从A地出发,需要在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
【解析】解:(1)vt=480,且全程速度限定不超过120km/h,
∴v与t之间的关系式为.
(2)∵8点至12点4(8分)的时间长为4.8h,8点至14点的时间长为6h,
∴将t=6代入中,得v=80,
将t=4.8代入中,得v=100.
∴小汽车行驶速度v的范围为80≤v≤100.
21.(2020秋 如皋市期末)为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
【解析】解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1=,
设药物燃烧后y关于x的函数关系式为y=(k2>0),
代入(8,6)得6=,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:(x>8),
∴;
(2)有效,理由如下:
把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
∴这次消毒是有效的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
