27.2 相似三角形 同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级下 27.2相似三角形同步练习
一.选择题
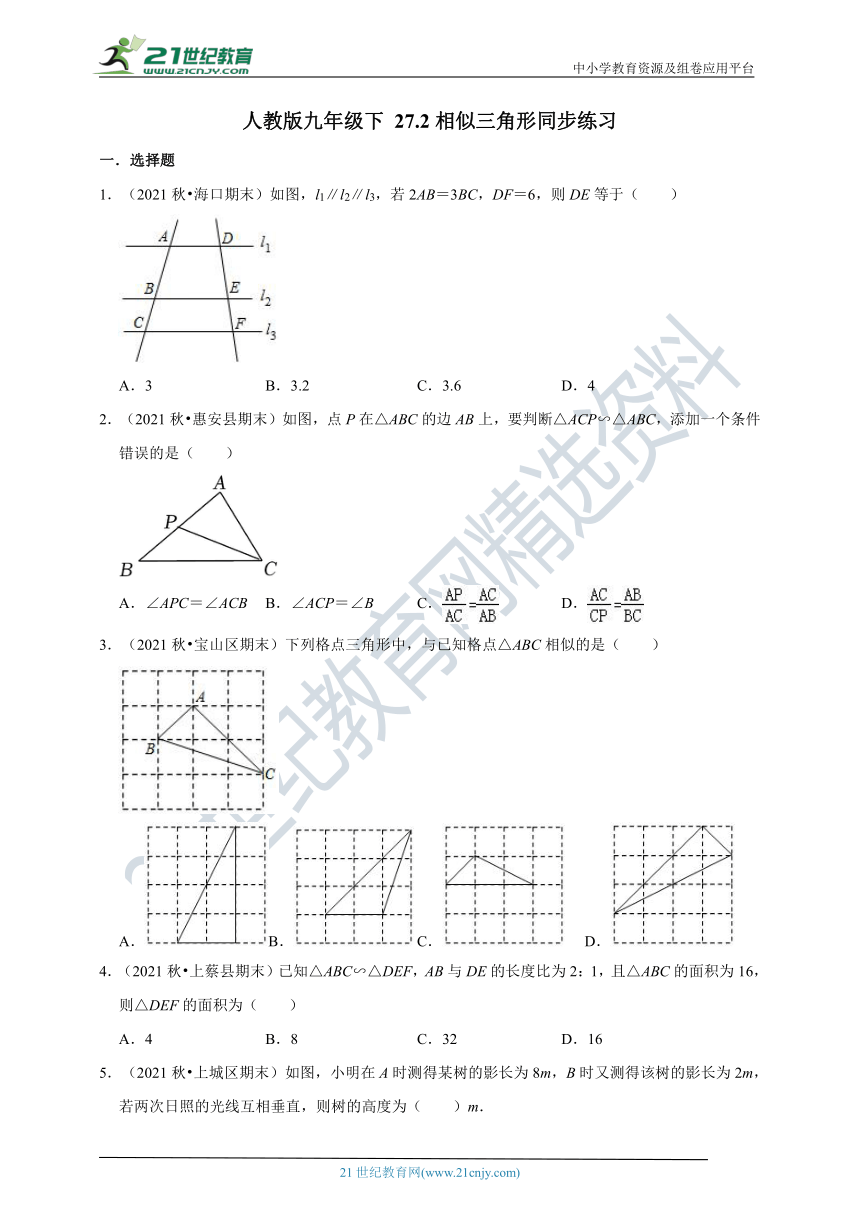
1.(2021秋 海口期末)如图,l1∥l2∥l3,若2AB=3BC,DF=6,则DE等于( )
A.3 B.3.2 C.3.6 D.4
2.(2021秋 惠安县期末)如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件错误的是( )
A.∠APC=∠ACB B.∠ACP=∠B C. D.
3.(2021秋 宝山区期末)下列格点三角形中,与已知格点△ABC相似的是( )
A.B. C. D.
4.(2021秋 上蔡县期末)已知△ABC∽△DEF,AB与DE的长度比为2:1,且△ABC的面积为16,则△DEF的面积为( )
A.4 B.8 C.32 D.16
5.(2021秋 上城区期末)如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
6.(2021秋 建华区期末)如图,M为线段AB上一点,AD与BC交于E,∠CMD=∠A=∠B,BC交MD于F,AD交MC于G,则图中相似三角形有( )
A.4对 B.3对 C.2对 D.1对
7.(2021秋 孟津县期末)如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似 B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似 D.甲与丙不相似,乙与丁不相似
8.(2021秋 鄞州区校级期末)如图,在平行四边形ABCD中,E、F是BC的三等分点,则EP:PQ:DQ=( )
A.1:1:2 B.3:2:5 C.5:3:12 D.4:3:9
9.(2021秋 南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A.4 B. C. D.5
10.(2021秋 余杭区期末)如图,在△ABC中,DE∥BC,EF∥AB,记S△ADE=S1,S△CEF=S2,S四边形BDEF=S3,则下列关于S1,S2,S3的关系式正确的是( )
A.S3=S1+S2 B.S3=2 C.S3= D.=+
二.填空题
11.(2021秋 蜀山区期末)如图,D是△ABC边AB延长线上一点,请添加一个条件: ,使△ACD∽△ABC.
12.(2021秋 兰考县期末)两个相似三角形的相似比为,较大三角形的周长是8;较小三角形的面积是6,则较大三角形的面积是 ;较小三角形的周长是 .
13.(2021秋 三水区期末)如图,小明为了测量树的高度CD,他在与树根同一水平面上的B处放置一块平面镜,然后他站在A处刚好能从镜中看到树顶D,已知A、B、C三点在同一直线上,且AB=2m,BC=8m.他的眼睛离地面的高度1.6m,则树的高度CD为 m.
14.(2021秋 锦州期末)如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE= .
15.(2021秋 黄浦区期末)如图,△ABC是边长为3的等边三角形,D、E分别是边BC、AC上的点,∠ADE=60°,如果BD=1,那么CE= .
16.(2021秋 达川区期末)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OB的中点,连接AE并延长交BC于点F,若△BEF的面积为1,则正方形ABCD的面积为 .
三.解答题
17.(2021秋 长春期末)如图,AD、BE是△ABC的高,连接DE.
(1)求证:△ACD∽△BCE;
(2)若点D是BC的中点,CE=6,BE=8,求AB的长.
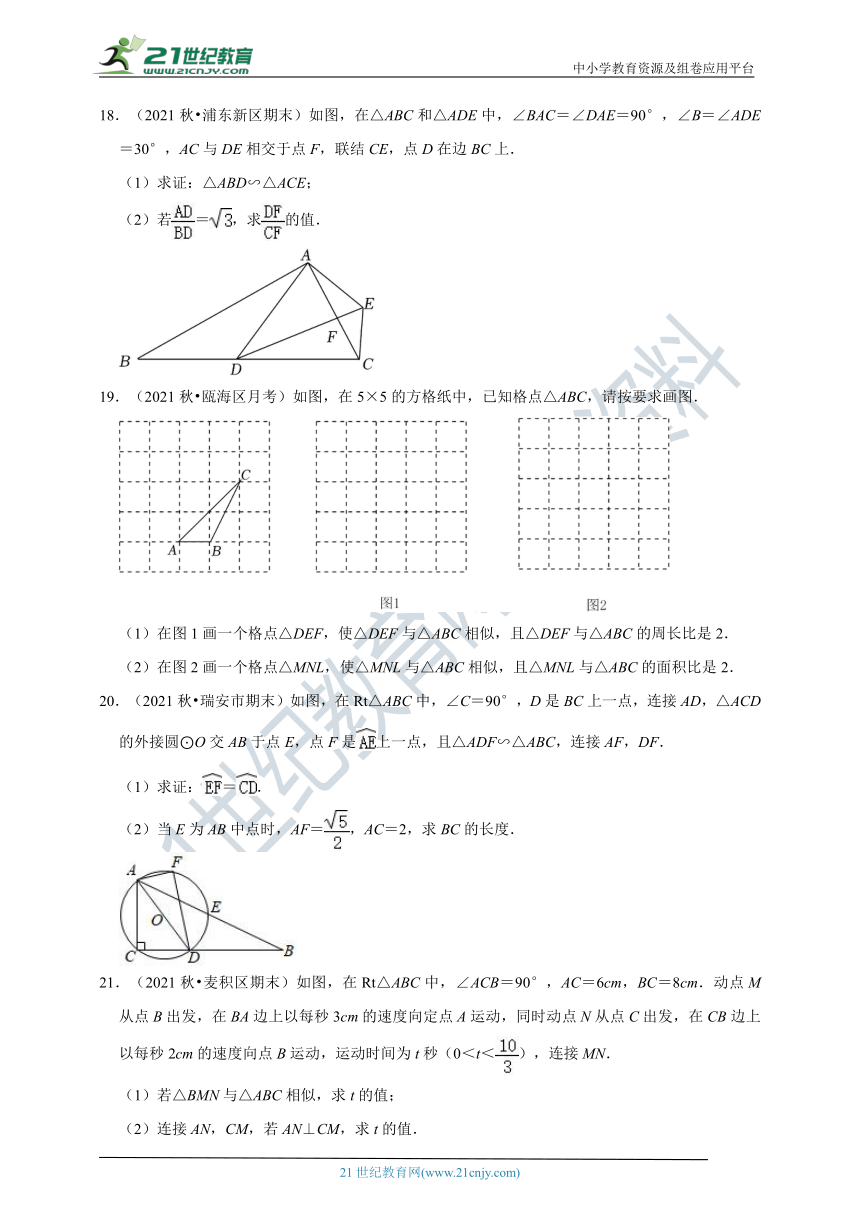
18.(2021秋 浦东新区期末)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠B=∠ADE=30°,AC与DE相交于点F,联结CE,点D在边BC上.
(1)求证:△ABD∽△ACE;
(2)若=,求的值.
19.(2021秋 瓯海区月考)如图,在5×5的方格纸中,已知格点△ABC,请按要求画图.
(1)在图1画一个格点△DEF,使△DEF与△ABC相似,且△DEF与△ABC的周长比是2.
(2)在图2画一个格点△MNL,使△MNL与△ABC相似,且△MNL与△ABC的面积比是2.
20.(2021秋 瑞安市期末)如图,在Rt△ABC中,∠C=90°,D是BC上一点,连接AD,△ACD的外接圆⊙O交AB于点E,点F是上一点,且△ADF∽△ABC,连接AF,DF.
(1)求证:=.
(2)当E为AB中点时,AF=,AC=2,求BC的长度.
21.(2021秋 麦积区期末)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
22.(2021秋 阜南县月考)一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
23.(2021秋 萧山区校级月考)如图,在菱形ABCD中,点E在BC边上(与点B、C不重合),连接AE交BD于点G.
(1)若AG=BG,AB=2,BD=3,求线段DG的长;
(2)设BC=kBE,△BGE的面积为S,△AGD和四边形CDGE的面积分别为S1和S2,把S1和S2分别用k、S的代数式表示;
(3)求的最大值.
答案与解析
一.选择题
1.(2021秋 海口期末)如图,l1∥l2∥l3,若2AB=3BC,DF=6,则DE等于( )
A.3 B.3.2 C.3.6 D.4
【解析】解:∵l1∥l2∥l3,2AB=3BC,
∴==,
∴=,
∵DF=6,
∴DE==3.6,
故选:C.
2.(2021秋 惠安县期末)如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件错误的是( )
A.∠APC=∠ACB B.∠ACP=∠B C. D.
【解析】解:A、∵∠APC=∠ACB,∠A=∠A,
∴△ACP∽△ABC,故此选项不符合题意;
B、∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,故此选项不符合题意;
C、∵,∠A=∠A,
∴△ACP∽△ABC,故此选项不符合题意;
D、两组边对应成比例的两个三角形不一定相似,故此选项符合题意.
故选:D.
3.(2021秋 宝山区期末)下列格点三角形中,与已知格点△ABC相似的是( )
A.B. C. D.
【解析】解:设小正方形的边长是1,
由勾股定理得:AB==,AC==2,BC==,
A.三角形的三边的长度分别为:=2,2,4,
∵=,=,=,
∴==,所以与格点△ABC相似,故本选项符合题意;
B.三角形的三边的长度分别为:2,=,=3,
∵=1,=,=,
∴≠≠,所以与格点△ABC不相似,故本选项不符合题意;
C.三角形的三边的长度分别为:=,=,3,
∵=1,=,=,
∴≠≠,所以与格点△ABC不相似,故本选项不符合题意;
D.三角形的三边的长度分别为:=,=3,=2,
∵=1,=,=,
∴≠≠,所以与格点△ABC不相似,故本选项不符合题意;
故选:A.
4.(2021秋 上蔡县期末)已知△ABC∽△DEF,AB与DE的长度比为2:1,且△ABC的面积为16,则△DEF的面积为( )
A.4 B.8 C.32 D.16
【解析】解:∵△ABC∽△DEF,AB与DE的长度比为2:1,
∴△ABC与△DEF的相似比为2:1,
∴△ABC与△DEF的面积比为4:1,
∵△ABC的面积为16,
∴△DEF的面积为16×=4,
故选:A.
5.(2021秋 上城区期末)如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
【解析】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴△EDC∽△CDF,
∴=,即DC2=ED FD=2×8=16,
解得CD=4m.
故选:B.
6.(2021秋 建华区期末)如图,M为线段AB上一点,AD与BC交于E,∠CMD=∠A=∠B,BC交MD于F,AD交MC于G,则图中相似三角形有( )
A.4对 B.3对 C.2对 D.1对
【解析】解:∵∠CMD=∠B,∠C=∠C,
∴△MCF∽△BCM,
∵∠CMD=∠A,∠D=∠D,
∴△AMD∽△MGD,
∵∠CMD=∠A=∠B,∠AMG=∠B+∠C,∠BFM=∠CMD+∠C,
∴∠AMG=∠BFM,
∴△AMG∽△BFM.
故选:B.
7.(2021秋 孟津县期末)如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似 B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似 D.甲与丙不相似,乙与丁不相似
【解析】解:∵OA:OB=OC:OD=2:3,
即,
而∠AOB=∠COD,
∴△AOB∽△COD,
∵,
∴,
∵∠AOC=∠BOD,
∴△AOC∽△BOD.
故选:A.
8.(2021秋 鄞州区校级期末)如图,在平行四边形ABCD中,E、F是BC的三等分点,则EP:PQ:DQ=( )
A.1:1:2 B.3:2:5 C.5:3:12 D.4:3:9
【解析】解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E、F是BC的三等分点,
∴AD=BC=3BE=3EF=3CF,
∵AD∥BC,
∴△AQD∽△CQE,△APD∽△FPE,
∴=,,
设DQ=3x,EQ=2x,则DE=5x,
∴DP=,EP=,
∴PQ=EQ﹣EP=2x﹣,
∴EP:PQ:DQ=5:3:12,
故选:C.
9.(2021秋 南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A.4 B. C. D.5
【解析】解:∵EF⊥FG,
∴∠EFB+∠GFC=90°,
∵四边形ABCD为矩形,
∴∠A=∠B=∠C=90°,AB=CD,
∴∠GFC+∠FGC=90°,
∴∠EFB=∠FGC,
∴△EFB∽△FGC,
∴,
∵BE=3,BF=2,FC=6,
∴,
∴CG=4,
同理可得△DAE∽△EBF,
∴,
∴,
∴AE=,
∴BA=AE+BE=+3=,
∴DG=CD﹣CG=﹣4=.
故选:B.
10.(2021秋 余杭区期末)如图,在△ABC中,DE∥BC,EF∥AB,记S△ADE=S1,S△CEF=S2,S四边形BDEF=S3,则下列关于S1,S2,S3的关系式正确的是( )
A.S3=S1+S2 B.S3=2 C.S3= D.=+
【解析】解:设AD=a,BD=b,DB与EF间的距离为h,
∵EF∥AB,DF∥BC,
∴四边形DBFE是平行四边形,
∴BD=EF=b,
∵DF∥BC,EF∥AB,
∴∠AFD=∠ACB,∠DAF=∠EFC,
∴△ADF∽△FEC,
∴==()2=,
∵S1=ah,
∴S2=,
∴S1S2=,
∴bh=2,
∵S3=bh,
∴S3=2.
故选:B.
二.填空题
11.(2021秋 蜀山区期末)如图,D是△ABC边AB延长线上一点,请添加一个条件: ∠ACD=∠ABC或∠ACB=∠D或 ,使△ACD∽△ABC.
【解析】解:添加:∠ACD=∠ABC.
∵∠A=∠A,∠ACD=∠ABC,
∴△ABC∽△ACD.
添加:∠ACB=∠D.
∵∠A=∠A,∠ACB=∠D,
∴△ABC∽△ACD.
添加:.
∵∠A=∠A,,
∴△ABC∽△ACD.
故答案为:∠ACD=∠ABC或∠ACB=∠D或.
12.(2021秋 兰考县期末)两个相似三角形的相似比为,较大三角形的周长是8;较小三角形的面积是6,则较大三角形的面积是 9 ;较小三角形的周长是 8 .
【解析】解:∵两个相似三角形的相似比为,
∴周长的比等于,面积的比等于3:2,
∵较大三角形的周长是8;较小三角形的面积是6,
∴则较大三角形的面积是9;较小三角形的周长是8,
故答案为:9,8.
13.(2021秋 三水区期末)如图,小明为了测量树的高度CD,他在与树根同一水平面上的B处放置一块平面镜,然后他站在A处刚好能从镜中看到树顶D,已知A、B、C三点在同一直线上,且AB=2m,BC=8m.他的眼睛离地面的高度1.6m,则树的高度CD为 6.4 m.
【解析】解:由题意可得:∠EBA=∠DBC,∠EAB=∠DCB,
故△EAB∽△DCB,
则=,
∵AB=2m,BC=8m,AE=1.6m,
∴=,
解得:DC=6.4,
故答案为:6.4.
14.(2021秋 锦州期末)如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE= 4或 .
【解析】解:∵△BDE∽△BCA或△BDE∽△BAC,
∴或,
∵BD=BC,BC=15,
∴BD=5,
∵AB=12,
∴或,
解得:BE=4或.
故答案为:4或.
15.(2021秋 黄浦区期末)如图,△ABC是边长为3的等边三角形,D、E分别是边BC、AC上的点,∠ADE=60°,如果BD=1,那么CE= .
【解析】解:∵△ABC为等边三角形,
∴∠B=∠C=60°,AB=BC=3,
∴CD=BC﹣BD=3﹣1=2,
∵∠ADC=∠B+∠BAD,
即∠ADE+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠D,
∴△CDE∽△BAD,
∴=,即=,
∴CE=.
故答案为:.
16.(2021秋 达川区期末)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OB的中点,连接AE并延长交BC于点F,若△BEF的面积为1,则正方形ABCD的面积为 24 .
【解析】解:∵四边形ABCD是正方形,
∴OB=OD,AD∥BC,
∴△EBF∽△EDA,
∵点E是OB的中点
∴OB=2BE,
∴DE:BE=3:1,
∴=3,
∴=9,
∵△BEF的面积为1,
∴S△AED=9,S△AEB=3S△BEF=3,
∴S△ABD=S△AED+S△AEB=9+3=12,
∴S正方形ABCD=2S△ABD=2×12=24.
故答案为:24.
三.解答题
17.(2021秋 长春期末)如图,AD、BE是△ABC的高,连接DE.
(1)求证:△ACD∽△BCE;
(2)若点D是BC的中点,CE=6,BE=8,求AB的长.
【解析】(1)证明:∵AD、BE是△ABC的高,
∴∠ADC=∠BEC=90°,
∵∠C=∠C,
∴△ACD∽△BCE;
(2)解:∵点D是BC的中点,AD⊥BC,
∴AB=AC,
在Rt△BEC中,
∵CE=6,BE=8,
∴BC===10,
∴CD=BC=5,
∵△ACD∽△BCE,
∴,
∴AD=,
∴AC===,
∴AB=AC=.
18.(2021秋 浦东新区期末)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠B=∠ADE=30°,AC与DE相交于点F,联结CE,点D在边BC上.
(1)求证:△ABD∽△ACE;
(2)若=,求的值.
【解析】(1)证明:∵∠ADE=∠DAE,∠B=∠ADE,
∴△BAC∽△DAE,
∴,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE;
(2)解:∵△ABD∽△ACE,
∴,
∵∠DAE=90°,∠ADE=30°,
∴=,
∴= ==3,
∵△ADF∽△ECF,
∴==3.
19.(2021秋 瓯海区月考)如图,在5×5的方格纸中,已知格点△ABC,请按要求画图.
(1)在图1画一个格点△DEF,使△DEF与△ABC相似,且△DEF与△ABC的周长比是2.
(2)在图2画一个格点△MNL,使△MNL与△ABC相似,且△MNL与△ABC的面积比是2.
【解析】解:(1)如图所示,△DEF即为所求.
(2)如图所示,△MNL即为所求.
20.(2021秋 瑞安市期末)如图,在Rt△ABC中,∠C=90°,D是BC上一点,连接AD,△ACD的外接圆⊙O交AB于点E,点F是上一点,且△ADF∽△ABC,连接AF,DF.
(1)求证:=.
(2)当E为AB中点时,AF=,AC=2,求BC的长度.
【解析】(1)证明:∵△ADF∽△ABC,
∴∠BAC=∠DAF,
∴∠CAD+∠BAD=∠BAD+∠EAF,
∴∠CAD=∠EAF,
∴;
(2)解:连接DE,
∵=,
∴DF=CE,
∵E为AB中点,
∴CE=AE=BE=AB,
∴DF=AB,
∵△ADF∽△ABC,
∴=,
∵AF=,AC=2,
∴=,
设DF=x,BC=4x,
∴AB=2x,
在Rt△ABC中:AC2+BC2=AB2,
∴4+16x2=20x2,
解得x=±1(负值舍去),
∴BC=4.
21.(2021秋 麦积区期末)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
【解析】解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB===10(cm),
由题意得BM=3 tcm,CN=2tcm,
∴BN=(8﹣2t)cm.
当△BMN∽△BAC时,=,即=,
解得:t=;
当△BMN∽△BCA时,=,即=,
解得:t=,
综上所述,△BMN与△ABC相似时,t的值为或;
(2)如图,过点M作MD⊥CB于点D,
∴∠BDM=∠ACB=90°,
∵∠B=∠B,
∴△BDM∽△BCA,
∴==,
∵AC=6cm,BC=8cm,BA=10cm,BM=3tcm,
∴DM=tcm,BD=tcm,
∴CD=(8﹣t)cm,
∵AN⊥CM,∠ACB=90°,
∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD.
∵MD⊥CB,
∴∠MDC=∠ACB=90°,
∴△CAN∽△DCM,
∴=,即=,
解得:t=.
22.(2021秋 阜南县月考)一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
【解析】解:设图1加工桌面长xcm,过点C作CM⊥AB,垂足为M,与GF相交于点N,
∵BC=75cm,AC=100cm,
∴BA===125(cm),
∵S△ACB=AB MC,
∴CM===60(cm),
∵GF∥DE,
∴△CGF∽△CAB,
∴,
∴.
∴.
∴x=;
设图2加工桌面长ycm,
∵FD∥BC,
∴Rt△AFD∽Rt△ACB,
∴,
,
解得y=,
∵,
∴图2加工方法得到的正方形面积较大.
23.(2021秋 萧山区校级月考)如图,在菱形ABCD中,点E在BC边上(与点B、C不重合),连接AE交BD于点G.
(1)若AG=BG,AB=2,BD=3,求线段DG的长;
(2)设BC=kBE,△BGE的面积为S,△AGD和四边形CDGE的面积分别为S1和S2,把S1和S2分别用k、S的代数式表示;
(3)求的最大值.
【解析】解:(1)∵AG=BG,
∴∠BAG=∠ABG,
∵四边形ABCD为菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠BAG=∠ADB,
∴△BAG∽△BDA,
∴,即=,
∴BG=,
∴DG=BD﹣BG=3﹣=;
(2)∵四边形ABCD为菱形,
∴BC=AD=kBE,AD∥BC,
∵AD∥BE,
∴∠DAE=∠BEA,∠ADG=∠BEG,
∴△ADG∽△EBG,
∴=()2=k2,==k,
∴S1=k2S,
∵==k,
∴S△ABG=,
∵△ABD的面积=△BDC的面积,
∴S2=S1+﹣S=k2S+kS﹣S=(k2+k﹣1)S;
(3)∵==1+﹣=﹣(﹣)2+,
∴的最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下 27.2相似三角形同步练习
一.选择题
1.(2021秋 海口期末)如图,l1∥l2∥l3,若2AB=3BC,DF=6,则DE等于( )
A.3 B.3.2 C.3.6 D.4
2.(2021秋 惠安县期末)如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件错误的是( )
A.∠APC=∠ACB B.∠ACP=∠B C. D.
3.(2021秋 宝山区期末)下列格点三角形中,与已知格点△ABC相似的是( )
A.B. C. D.
4.(2021秋 上蔡县期末)已知△ABC∽△DEF,AB与DE的长度比为2:1,且△ABC的面积为16,则△DEF的面积为( )
A.4 B.8 C.32 D.16
5.(2021秋 上城区期末)如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
6.(2021秋 建华区期末)如图,M为线段AB上一点,AD与BC交于E,∠CMD=∠A=∠B,BC交MD于F,AD交MC于G,则图中相似三角形有( )
A.4对 B.3对 C.2对 D.1对
7.(2021秋 孟津县期末)如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似 B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似 D.甲与丙不相似,乙与丁不相似
8.(2021秋 鄞州区校级期末)如图,在平行四边形ABCD中,E、F是BC的三等分点,则EP:PQ:DQ=( )
A.1:1:2 B.3:2:5 C.5:3:12 D.4:3:9
9.(2021秋 南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A.4 B. C. D.5
10.(2021秋 余杭区期末)如图,在△ABC中,DE∥BC,EF∥AB,记S△ADE=S1,S△CEF=S2,S四边形BDEF=S3,则下列关于S1,S2,S3的关系式正确的是( )
A.S3=S1+S2 B.S3=2 C.S3= D.=+
二.填空题
11.(2021秋 蜀山区期末)如图,D是△ABC边AB延长线上一点,请添加一个条件: ,使△ACD∽△ABC.
12.(2021秋 兰考县期末)两个相似三角形的相似比为,较大三角形的周长是8;较小三角形的面积是6,则较大三角形的面积是 ;较小三角形的周长是 .
13.(2021秋 三水区期末)如图,小明为了测量树的高度CD,他在与树根同一水平面上的B处放置一块平面镜,然后他站在A处刚好能从镜中看到树顶D,已知A、B、C三点在同一直线上,且AB=2m,BC=8m.他的眼睛离地面的高度1.6m,则树的高度CD为 m.
14.(2021秋 锦州期末)如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE= .
15.(2021秋 黄浦区期末)如图,△ABC是边长为3的等边三角形,D、E分别是边BC、AC上的点,∠ADE=60°,如果BD=1,那么CE= .
16.(2021秋 达川区期末)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OB的中点,连接AE并延长交BC于点F,若△BEF的面积为1,则正方形ABCD的面积为 .
三.解答题
17.(2021秋 长春期末)如图,AD、BE是△ABC的高,连接DE.
(1)求证:△ACD∽△BCE;
(2)若点D是BC的中点,CE=6,BE=8,求AB的长.
18.(2021秋 浦东新区期末)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠B=∠ADE=30°,AC与DE相交于点F,联结CE,点D在边BC上.
(1)求证:△ABD∽△ACE;
(2)若=,求的值.
19.(2021秋 瓯海区月考)如图,在5×5的方格纸中,已知格点△ABC,请按要求画图.
(1)在图1画一个格点△DEF,使△DEF与△ABC相似,且△DEF与△ABC的周长比是2.
(2)在图2画一个格点△MNL,使△MNL与△ABC相似,且△MNL与△ABC的面积比是2.
20.(2021秋 瑞安市期末)如图,在Rt△ABC中,∠C=90°,D是BC上一点,连接AD,△ACD的外接圆⊙O交AB于点E,点F是上一点,且△ADF∽△ABC,连接AF,DF.
(1)求证:=.
(2)当E为AB中点时,AF=,AC=2,求BC的长度.
21.(2021秋 麦积区期末)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
22.(2021秋 阜南县月考)一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
23.(2021秋 萧山区校级月考)如图,在菱形ABCD中,点E在BC边上(与点B、C不重合),连接AE交BD于点G.
(1)若AG=BG,AB=2,BD=3,求线段DG的长;
(2)设BC=kBE,△BGE的面积为S,△AGD和四边形CDGE的面积分别为S1和S2,把S1和S2分别用k、S的代数式表示;
(3)求的最大值.
答案与解析
一.选择题
1.(2021秋 海口期末)如图,l1∥l2∥l3,若2AB=3BC,DF=6,则DE等于( )
A.3 B.3.2 C.3.6 D.4
【解析】解:∵l1∥l2∥l3,2AB=3BC,
∴==,
∴=,
∵DF=6,
∴DE==3.6,
故选:C.
2.(2021秋 惠安县期末)如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件错误的是( )
A.∠APC=∠ACB B.∠ACP=∠B C. D.
【解析】解:A、∵∠APC=∠ACB,∠A=∠A,
∴△ACP∽△ABC,故此选项不符合题意;
B、∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,故此选项不符合题意;
C、∵,∠A=∠A,
∴△ACP∽△ABC,故此选项不符合题意;
D、两组边对应成比例的两个三角形不一定相似,故此选项符合题意.
故选:D.
3.(2021秋 宝山区期末)下列格点三角形中,与已知格点△ABC相似的是( )
A.B. C. D.
【解析】解:设小正方形的边长是1,
由勾股定理得:AB==,AC==2,BC==,
A.三角形的三边的长度分别为:=2,2,4,
∵=,=,=,
∴==,所以与格点△ABC相似,故本选项符合题意;
B.三角形的三边的长度分别为:2,=,=3,
∵=1,=,=,
∴≠≠,所以与格点△ABC不相似,故本选项不符合题意;
C.三角形的三边的长度分别为:=,=,3,
∵=1,=,=,
∴≠≠,所以与格点△ABC不相似,故本选项不符合题意;
D.三角形的三边的长度分别为:=,=3,=2,
∵=1,=,=,
∴≠≠,所以与格点△ABC不相似,故本选项不符合题意;
故选:A.
4.(2021秋 上蔡县期末)已知△ABC∽△DEF,AB与DE的长度比为2:1,且△ABC的面积为16,则△DEF的面积为( )
A.4 B.8 C.32 D.16
【解析】解:∵△ABC∽△DEF,AB与DE的长度比为2:1,
∴△ABC与△DEF的相似比为2:1,
∴△ABC与△DEF的面积比为4:1,
∵△ABC的面积为16,
∴△DEF的面积为16×=4,
故选:A.
5.(2021秋 上城区期末)如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
【解析】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴△EDC∽△CDF,
∴=,即DC2=ED FD=2×8=16,
解得CD=4m.
故选:B.
6.(2021秋 建华区期末)如图,M为线段AB上一点,AD与BC交于E,∠CMD=∠A=∠B,BC交MD于F,AD交MC于G,则图中相似三角形有( )
A.4对 B.3对 C.2对 D.1对
【解析】解:∵∠CMD=∠B,∠C=∠C,
∴△MCF∽△BCM,
∵∠CMD=∠A,∠D=∠D,
∴△AMD∽△MGD,
∵∠CMD=∠A=∠B,∠AMG=∠B+∠C,∠BFM=∠CMD+∠C,
∴∠AMG=∠BFM,
∴△AMG∽△BFM.
故选:B.
7.(2021秋 孟津县期末)如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似 B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似 D.甲与丙不相似,乙与丁不相似
【解析】解:∵OA:OB=OC:OD=2:3,
即,
而∠AOB=∠COD,
∴△AOB∽△COD,
∵,
∴,
∵∠AOC=∠BOD,
∴△AOC∽△BOD.
故选:A.
8.(2021秋 鄞州区校级期末)如图,在平行四边形ABCD中,E、F是BC的三等分点,则EP:PQ:DQ=( )
A.1:1:2 B.3:2:5 C.5:3:12 D.4:3:9
【解析】解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E、F是BC的三等分点,
∴AD=BC=3BE=3EF=3CF,
∵AD∥BC,
∴△AQD∽△CQE,△APD∽△FPE,
∴=,,
设DQ=3x,EQ=2x,则DE=5x,
∴DP=,EP=,
∴PQ=EQ﹣EP=2x﹣,
∴EP:PQ:DQ=5:3:12,
故选:C.
9.(2021秋 南京期末)如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A.4 B. C. D.5
【解析】解:∵EF⊥FG,
∴∠EFB+∠GFC=90°,
∵四边形ABCD为矩形,
∴∠A=∠B=∠C=90°,AB=CD,
∴∠GFC+∠FGC=90°,
∴∠EFB=∠FGC,
∴△EFB∽△FGC,
∴,
∵BE=3,BF=2,FC=6,
∴,
∴CG=4,
同理可得△DAE∽△EBF,
∴,
∴,
∴AE=,
∴BA=AE+BE=+3=,
∴DG=CD﹣CG=﹣4=.
故选:B.
10.(2021秋 余杭区期末)如图,在△ABC中,DE∥BC,EF∥AB,记S△ADE=S1,S△CEF=S2,S四边形BDEF=S3,则下列关于S1,S2,S3的关系式正确的是( )
A.S3=S1+S2 B.S3=2 C.S3= D.=+
【解析】解:设AD=a,BD=b,DB与EF间的距离为h,
∵EF∥AB,DF∥BC,
∴四边形DBFE是平行四边形,
∴BD=EF=b,
∵DF∥BC,EF∥AB,
∴∠AFD=∠ACB,∠DAF=∠EFC,
∴△ADF∽△FEC,
∴==()2=,
∵S1=ah,
∴S2=,
∴S1S2=,
∴bh=2,
∵S3=bh,
∴S3=2.
故选:B.
二.填空题
11.(2021秋 蜀山区期末)如图,D是△ABC边AB延长线上一点,请添加一个条件: ∠ACD=∠ABC或∠ACB=∠D或 ,使△ACD∽△ABC.
【解析】解:添加:∠ACD=∠ABC.
∵∠A=∠A,∠ACD=∠ABC,
∴△ABC∽△ACD.
添加:∠ACB=∠D.
∵∠A=∠A,∠ACB=∠D,
∴△ABC∽△ACD.
添加:.
∵∠A=∠A,,
∴△ABC∽△ACD.
故答案为:∠ACD=∠ABC或∠ACB=∠D或.
12.(2021秋 兰考县期末)两个相似三角形的相似比为,较大三角形的周长是8;较小三角形的面积是6,则较大三角形的面积是 9 ;较小三角形的周长是 8 .
【解析】解:∵两个相似三角形的相似比为,
∴周长的比等于,面积的比等于3:2,
∵较大三角形的周长是8;较小三角形的面积是6,
∴则较大三角形的面积是9;较小三角形的周长是8,
故答案为:9,8.
13.(2021秋 三水区期末)如图,小明为了测量树的高度CD,他在与树根同一水平面上的B处放置一块平面镜,然后他站在A处刚好能从镜中看到树顶D,已知A、B、C三点在同一直线上,且AB=2m,BC=8m.他的眼睛离地面的高度1.6m,则树的高度CD为 6.4 m.
【解析】解:由题意可得:∠EBA=∠DBC,∠EAB=∠DCB,
故△EAB∽△DCB,
则=,
∵AB=2m,BC=8m,AE=1.6m,
∴=,
解得:DC=6.4,
故答案为:6.4.
14.(2021秋 锦州期末)如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE= 4或 .
【解析】解:∵△BDE∽△BCA或△BDE∽△BAC,
∴或,
∵BD=BC,BC=15,
∴BD=5,
∵AB=12,
∴或,
解得:BE=4或.
故答案为:4或.
15.(2021秋 黄浦区期末)如图,△ABC是边长为3的等边三角形,D、E分别是边BC、AC上的点,∠ADE=60°,如果BD=1,那么CE= .
【解析】解:∵△ABC为等边三角形,
∴∠B=∠C=60°,AB=BC=3,
∴CD=BC﹣BD=3﹣1=2,
∵∠ADC=∠B+∠BAD,
即∠ADE+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠D,
∴△CDE∽△BAD,
∴=,即=,
∴CE=.
故答案为:.
16.(2021秋 达川区期末)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OB的中点,连接AE并延长交BC于点F,若△BEF的面积为1,则正方形ABCD的面积为 24 .
【解析】解:∵四边形ABCD是正方形,
∴OB=OD,AD∥BC,
∴△EBF∽△EDA,
∵点E是OB的中点
∴OB=2BE,
∴DE:BE=3:1,
∴=3,
∴=9,
∵△BEF的面积为1,
∴S△AED=9,S△AEB=3S△BEF=3,
∴S△ABD=S△AED+S△AEB=9+3=12,
∴S正方形ABCD=2S△ABD=2×12=24.
故答案为:24.
三.解答题
17.(2021秋 长春期末)如图,AD、BE是△ABC的高,连接DE.
(1)求证:△ACD∽△BCE;
(2)若点D是BC的中点,CE=6,BE=8,求AB的长.
【解析】(1)证明:∵AD、BE是△ABC的高,
∴∠ADC=∠BEC=90°,
∵∠C=∠C,
∴△ACD∽△BCE;
(2)解:∵点D是BC的中点,AD⊥BC,
∴AB=AC,
在Rt△BEC中,
∵CE=6,BE=8,
∴BC===10,
∴CD=BC=5,
∵△ACD∽△BCE,
∴,
∴AD=,
∴AC===,
∴AB=AC=.
18.(2021秋 浦东新区期末)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠B=∠ADE=30°,AC与DE相交于点F,联结CE,点D在边BC上.
(1)求证:△ABD∽△ACE;
(2)若=,求的值.
【解析】(1)证明:∵∠ADE=∠DAE,∠B=∠ADE,
∴△BAC∽△DAE,
∴,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE;
(2)解:∵△ABD∽△ACE,
∴,
∵∠DAE=90°,∠ADE=30°,
∴=,
∴= ==3,
∵△ADF∽△ECF,
∴==3.
19.(2021秋 瓯海区月考)如图,在5×5的方格纸中,已知格点△ABC,请按要求画图.
(1)在图1画一个格点△DEF,使△DEF与△ABC相似,且△DEF与△ABC的周长比是2.
(2)在图2画一个格点△MNL,使△MNL与△ABC相似,且△MNL与△ABC的面积比是2.
【解析】解:(1)如图所示,△DEF即为所求.
(2)如图所示,△MNL即为所求.
20.(2021秋 瑞安市期末)如图,在Rt△ABC中,∠C=90°,D是BC上一点,连接AD,△ACD的外接圆⊙O交AB于点E,点F是上一点,且△ADF∽△ABC,连接AF,DF.
(1)求证:=.
(2)当E为AB中点时,AF=,AC=2,求BC的长度.
【解析】(1)证明:∵△ADF∽△ABC,
∴∠BAC=∠DAF,
∴∠CAD+∠BAD=∠BAD+∠EAF,
∴∠CAD=∠EAF,
∴;
(2)解:连接DE,
∵=,
∴DF=CE,
∵E为AB中点,
∴CE=AE=BE=AB,
∴DF=AB,
∵△ADF∽△ABC,
∴=,
∵AF=,AC=2,
∴=,
设DF=x,BC=4x,
∴AB=2x,
在Rt△ABC中:AC2+BC2=AB2,
∴4+16x2=20x2,
解得x=±1(负值舍去),
∴BC=4.
21.(2021秋 麦积区期末)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
【解析】解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB===10(cm),
由题意得BM=3 tcm,CN=2tcm,
∴BN=(8﹣2t)cm.
当△BMN∽△BAC时,=,即=,
解得:t=;
当△BMN∽△BCA时,=,即=,
解得:t=,
综上所述,△BMN与△ABC相似时,t的值为或;
(2)如图,过点M作MD⊥CB于点D,
∴∠BDM=∠ACB=90°,
∵∠B=∠B,
∴△BDM∽△BCA,
∴==,
∵AC=6cm,BC=8cm,BA=10cm,BM=3tcm,
∴DM=tcm,BD=tcm,
∴CD=(8﹣t)cm,
∵AN⊥CM,∠ACB=90°,
∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD.
∵MD⊥CB,
∴∠MDC=∠ACB=90°,
∴△CAN∽△DCM,
∴=,即=,
解得:t=.
22.(2021秋 阜南县月考)一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
【解析】解:设图1加工桌面长xcm,过点C作CM⊥AB,垂足为M,与GF相交于点N,
∵BC=75cm,AC=100cm,
∴BA===125(cm),
∵S△ACB=AB MC,
∴CM===60(cm),
∵GF∥DE,
∴△CGF∽△CAB,
∴,
∴.
∴.
∴x=;
设图2加工桌面长ycm,
∵FD∥BC,
∴Rt△AFD∽Rt△ACB,
∴,
,
解得y=,
∵,
∴图2加工方法得到的正方形面积较大.
23.(2021秋 萧山区校级月考)如图,在菱形ABCD中,点E在BC边上(与点B、C不重合),连接AE交BD于点G.
(1)若AG=BG,AB=2,BD=3,求线段DG的长;
(2)设BC=kBE,△BGE的面积为S,△AGD和四边形CDGE的面积分别为S1和S2,把S1和S2分别用k、S的代数式表示;
(3)求的最大值.
【解析】解:(1)∵AG=BG,
∴∠BAG=∠ABG,
∵四边形ABCD为菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠BAG=∠ADB,
∴△BAG∽△BDA,
∴,即=,
∴BG=,
∴DG=BD﹣BG=3﹣=;
(2)∵四边形ABCD为菱形,
∴BC=AD=kBE,AD∥BC,
∵AD∥BE,
∴∠DAE=∠BEA,∠ADG=∠BEG,
∴△ADG∽△EBG,
∴=()2=k2,==k,
∴S1=k2S,
∵==k,
∴S△ABG=,
∵△ABD的面积=△BDC的面积,
∴S2=S1+﹣S=k2S+kS﹣S=(k2+k﹣1)S;
(3)∵==1+﹣=﹣(﹣)2+,
∴的最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
