27.3 位似 同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级下 27.3位似同步练习
一.选择题
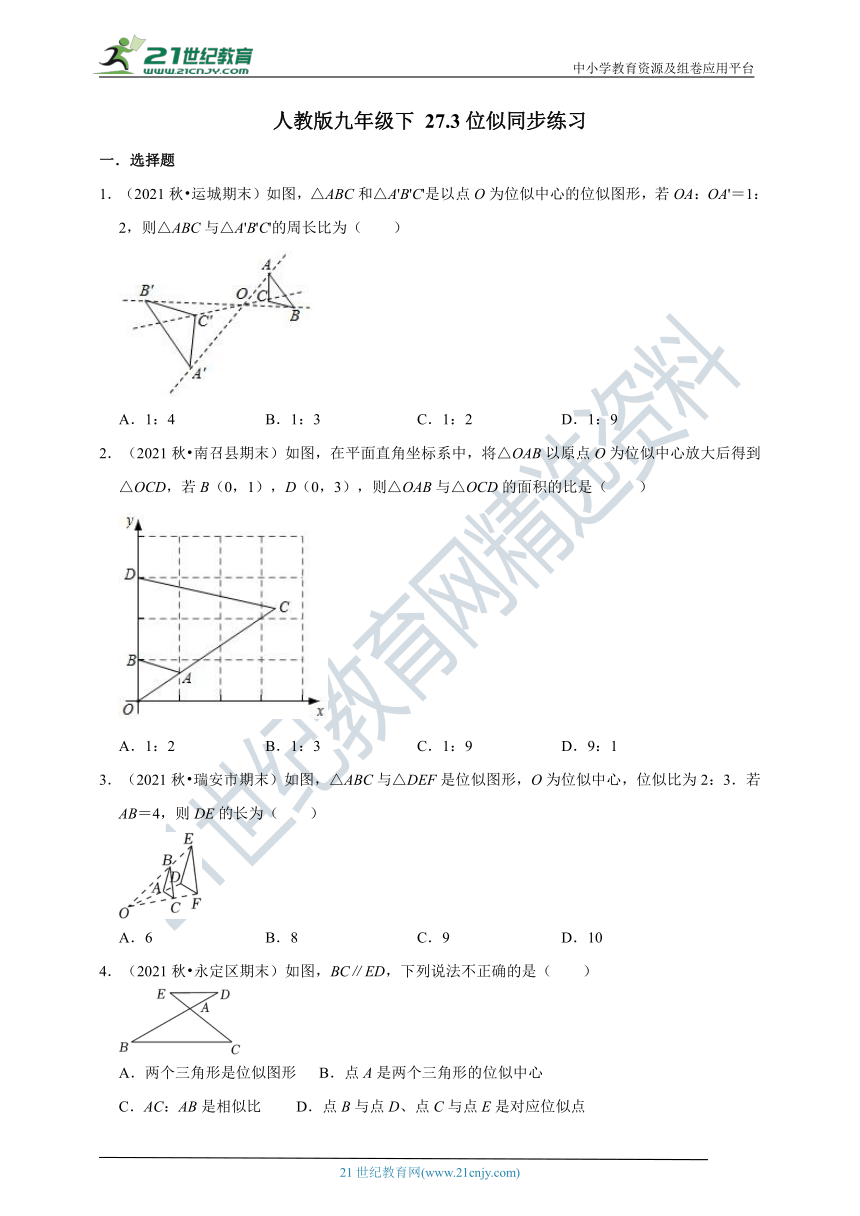
1.(2021秋 运城期末)如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,若OA:OA'=1:2,则△ABC与△A'B'C'的周长比为( )
A.1:4 B.1:3 C.1:2 D.1:9
2.(2021秋 南召县期末)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的面积的比是( )
A.1:2 B.1:3 C.1:9 D.9:1
3.(2021秋 瑞安市期末)如图,△ABC与△DEF是位似图形,O为位似中心,位似比为2:3.若AB=4,则DE的长为( )
A.6 B.8 C.9 D.10
4.(2021秋 永定区期末)如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形 B.点A是两个三角形的位似中心
C.AC:AB是相似比 D.点B与点D、点C与点E是对应位似点
5.(2021秋 邵东市期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
6.(2021秋 道县期末)下列说法正确的是( )
A.相似图形一定是位似图形 B.一条线段的黄金分割点只有一个
C.两个边数相同的正多边形是相似图形
D.相似三角形对应角的平分线的比等于对应边上高的比的平方
7.(2021秋 九龙坡区校级期末)如图,四边形ABCD和四边形A1B1C1D1是以点O为位似中心的位似图形,若OA:OA1=:2,则四边形ABCD与四边形A1B1C1D1的面积比为( )
A. B.3:4 C.3:2 D.9:4
8.(2021秋 仁寿县期末)点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法中错误的是( )
A.EF=BC B.EF与AD互相平分 C.△AFE是△ABC的位似图形 D.
9.(2021秋 太原期末)如图,在平面直角坐标系中,四边形ABCD与四边形A'B'C'D'是位似图形.位似中心到点D和点D'的距离的比值是( )
A.2 B. C. D.
二.填空题
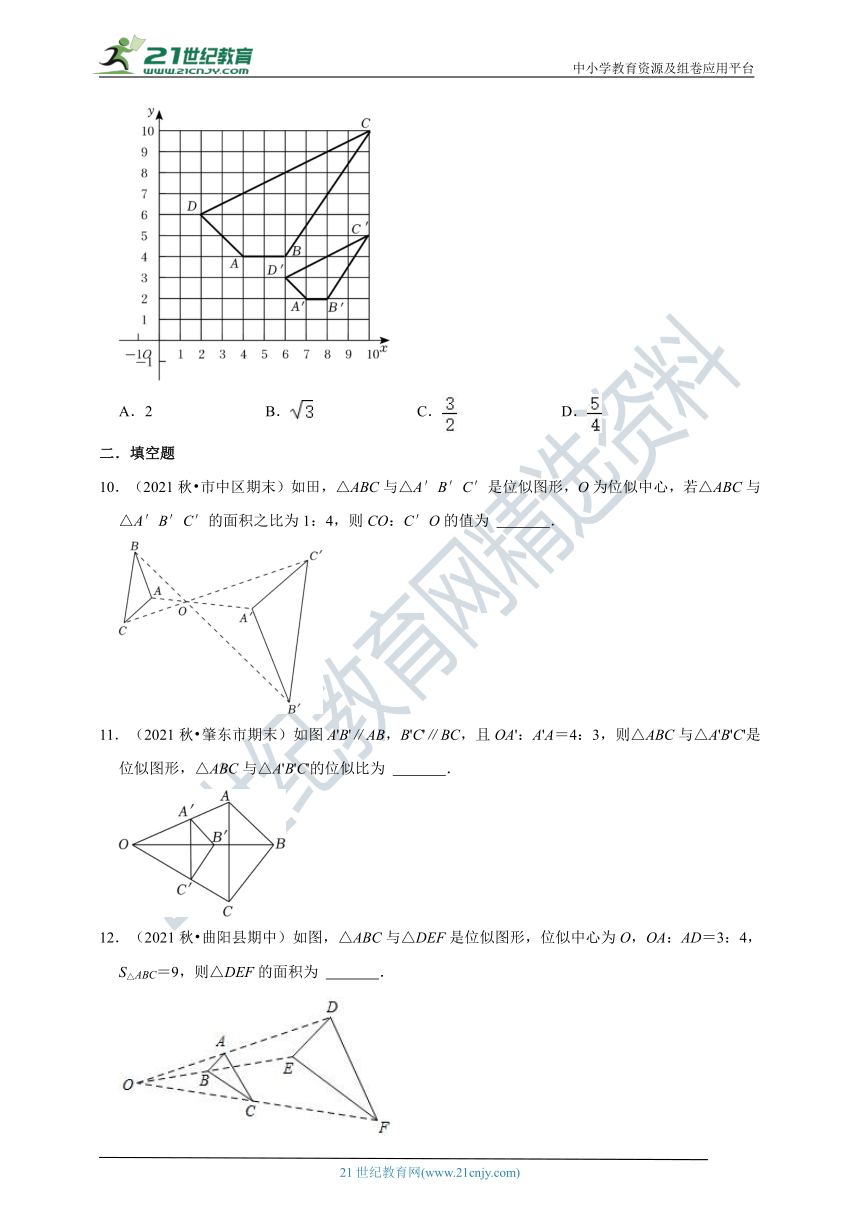
10.(2021秋 市中区期末)如田,△ABC与△A′B′C′是位似图形,O为位似中心,若△ABC与△A′B′C′的面积之比为1:4,则CO:C′O的值为 .
11.(2021秋 肇东市期末)如图A'B'∥AB,B'C'∥BC,且OA':A'A=4:3,则△ABC与△A'B'C'是位似图形,△ABC与△A'B'C'的位似比为 .
12.(2021秋 曲阳县期中)如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为 .
13.(2021秋 大东区期末)线段AB、CD在平面直角坐标系中的网格位置.如图所示,O为坐标原点,A、B、C、D均在格点上,线段AB、CD是位似图形,位似中心的坐标是 .
14.(2021秋 揭西县期末)在平面直角坐标系中,△ABC中点A的坐标是(2,3),以原点O为位似中心把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,则点A的对应点A′的坐标为 .
15.(2021秋 晋江市期中)五边形ABCDE位似于五边形A'B'C'D'E',它们的面积比为4:9,已知位似中心O到A点的距离为6,那么O到A'的距离为 .
16.(2021秋 新乡期末)如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,且△ABC和△A'B'C的周长之比为1:2,点C的坐标为(﹣1,0),若点B的对应点B'的横坐标为5,则点B的横坐标为 .
三.解答题
17.(2020秋 六盘水期末)在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(2,0),B(2,2),C(0,4).
(1)请画出四边形OABC关于y轴对称的四边形OEDC;
(2)以原点O为位似中心,请画出一个五边形A1B1C1D1E1与五边形ABCDE位似,且相似比是2:1.
18.(2021秋 泉州期末)如图,在边长均为1的正方形网格中,△ABC的顶点均在格点上,O为直角坐标系的原点,△ABC三个顶点坐标分别为A(1,2)、B(0,1)、C(2,0).
(1)以O为位似中心,将△ABC放大为△A1B1C1,使得△A1B1C1与△ABC的相似比为2:1,请在网格中画出△A1B1C1(其中A1在第三象限内);
(2)直接写出(1)中点A1、B1、C1的坐标.
19.(2021秋 新都区期末)如图,在边长为1的小正方形网格中.
(1)△ABC向右平移6个单位长度,再向上平移5个单位长度后得到△A1B1C1,请在网格中画出△A1B1C1,其中B1的坐标为 ;
(2)以点A为位似中心,将△ABC放大为原来的2倍,得到△AB2C2,请在网格中画出△AB2C2;
(3)连接AB1,B1B2,则△AB1B2的面积为 .
20.(2021秋 涡阳县期末)如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出△ABC关于x轴对称的△A'B'C';
(2)以坐标原点为位似中心在图中的网格中作出△A'B'C'的位似图形△A″B″C″,使△A'B'C'与△A″B″C″的位似比为1:2;
(3)若△ABC的面积为3.5平方单位,求出△A″B″C″的面积.
21.(2021秋 振兴区校级月考)如图,在平面直角坐标系中,五边形A'B'C'D'E'是五边形ABCDE的位似图形,但图形并不完整.已知A点坐标(2,5),A′点坐标(2,3).
(1)请在图中标注位似中心P,并直接写出P点坐标 ;
(2)请把两个五边形补充完整;
(3)请写出五边形A'B'C'D'E'与五边形ABCDE的位似比 .
答案与解析
一.选择题
1.(2021秋 运城期末)如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,若OA:OA'=1:2,则△ABC与△A'B'C'的周长比为( )
A.1:4 B.1:3 C.1:2 D.1:9
【解析】解:∵OA:OA'=1:2,
∴AC:A′C′=1:2,
∴△ABC与△A′B′C′的相似比是1:2,
∴△ABC与△A′B′C′的周长比为1:2,
故选:C.
2.(2021秋 南召县期末)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的面积的比是( )
A.1:2 B.1:3 C.1:9 D.9:1
【解析】解:∵B(0,1),D(0,3),
∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
∴△OAB与△OCD的面积的比是1:9.
故选:C.
3.(2021秋 瑞安市期末)如图,△ABC与△DEF是位似图形,O为位似中心,位似比为2:3.若AB=4,则DE的长为( )
A.6 B.8 C.9 D.10
【解析】解:∵△ABC与△DEF是位似图形,位似比为2:3,
∴AB:DE=2:3.
∵AB=4,
∴DE=6.
故选:A.
4.(2021秋 永定区期末)如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形 B.点A是两个三角形的位似中心
C.AC:AB是相似比 D.点B与点D、点C与点E是对应位似点
【解析】解:A、两个三角形是位似图形,本选项说法正确,不符合题意;
B、点A是两个三角形的位似中心,本选项说法正确,不符合题意;
C、AC:AE是相似比,故本选项说法不正确,符合题意;
D、点B与点D、点C与点E是对应位似点,本选项说法正确,不符合题意;
故选:C.
5.(2021秋 邵东市期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
【解析】解:∵以原点O为位似中心,相似比为,把△EFO缩小,点E(﹣4,2),
∴点E的对应点E′的坐标是(﹣4×,2×)或(﹣4×(﹣),2×(﹣)),即(﹣2,1)或(2,﹣1),
故选:D.
6.(2021秋 道县期末)下列说法正确的是( )
A.相似图形一定是位似图形 B.一条线段的黄金分割点只有一个
C.两个边数相同的正多边形是相似图形
D.相似三角形对应角的平分线的比等于对应边上高的比的平方
【解析】解:A、位似图形一定是相似图形,但相似图形不一定是位似图形,本选项说法错误,不符合题意;
B、一条线段的黄金分割点有两个,本选项说法错误,不符合题意;
C、两个边数相同的正多边形是相似图形,本选项说法正确,符合题意;
D、相似三角形对应角的平分线的比等于对应边上高的比,本选项说法错误,不符合题意;
故选:C.
7.(2021秋 九龙坡区校级期末)如图,四边形ABCD和四边形A1B1C1D1是以点O为位似中心的位似图形,若OA:OA1=:2,则四边形ABCD与四边形A1B1C1D1的面积比为( )
A. B.3:4 C.3:2 D.9:4
【解析】解:∵四边形ABCD和四边形A1B1C1D1是以点O为位似中心的位似图形,OA:OA1=:2,
∴四边形ABCD和四边形A1B1C1D1的位似比为:2,
∴四边形ABCD与四边形A1B1C1D1的面积比3:4,
故选:B.
8.(2021秋 仁寿县期末)点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法中错误的是( )
A.EF=BC B.EF与AD互相平分 C.△AFE是△ABC的位似图形 D.
【解析】解:A、∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴EF=BC,本选项说法正确,不符合题意;
B、∵点D、E、F分别是△ABC各边的中点,
∴EF∥BC,ED∥AC,
∴四边形AEDF为平行四边形,
∴EF与AD互相平分,本选项说法正确,不符合题意;
C、∵EF∥BC,
∴△AEF∽△ABC,
∵△AFE和△ABC对应点的连线都经过同一点、对应边平行,
∴△AFE是△ABC的位似图形,本选项说法正确,不符合题意;
D、∵ED∥AC,
∴△BDE∽△BCA,
∴=,故本选项说法错误,符合题意;
故选:D.
9.(2021秋 太原期末)如图,在平面直角坐标系中,四边形ABCD与四边形A'B'C'D'是位似图形.位似中心到点D和点D'的距离的比值是( )
A.2 B. C. D.
【解析】解:如图所示:点P即为位似中心,位似中心到点D和点D'的距离的比值是:PD:PD′=2:1=2.
故选:A.
二.填空题
10.(2021秋 市中区期末)如田,△ABC与△A′B′C′是位似图形,O为位似中心,若△ABC与△A′B′C′的面积之比为1:4,则CO:C′O的值为 1:2 .
【解析】解:如图,△ABC与△A′B′C′是位似图形,O是位似中心,
∵△ABC与△A′B′C′的面积之比为1:4,
∴△ABC与△A′B′C′的相似比为1:2.
∵△ABC与△A′B′C′是位似图形,
∴△BCO∽△B′C′O′.
∴CO:C′O=BC:B′C′=1:2.
故答案为:1:2.
11.(2021秋 肇东市期末)如图A'B'∥AB,B'C'∥BC,且OA':A'A=4:3,则△ABC与△A'B'C'是位似图形,△ABC与△A'B'C'的位似比为 7:4 .
【解析】解:∵OA':A'A=4:3,
∴OA:OA′=7:4,
∵△ABC与△A'B'C'是位似图形,
∴A′B′∥AB,
∴△OAB∽△OA′B′,
∴==,
∴△ABC与△A'B'C'的位似比=7:4,
故答案为:7:4.
12.(2021秋 曲阳县期中)如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为 49 .
【解析】解:∵OA:AD=3:4,
∴OA:OD=3:7,
∵△ABC与△DEF是位似图形,
∴AB∥DE,
∴△OAB∽△ODE,
∴==,
∴=()2=,
∵S△ABC=9,
∴△DEF的面积为49,
故答案为:49.
13.(2021秋 大东区期末)线段AB、CD在平面直角坐标系中的网格位置.如图所示,O为坐标原点,A、B、C、D均在格点上,线段AB、CD是位似图形,位似中心的坐标是 (0,0)或(,4) .
【解析】解:当点A和点C为对应点,点B和点D为对应点时,延长CA、BD交于点O,
则位似中心的坐标是(0,0),
当点A和点D为对应点,点B和点C为对应点时,连接AD、BC交于点P,
则点P为位似中心,
∵线段AB、CD是位似图形,
∴AB∥CD,
∴△PAB∽△PDC,
∴===,即=,
∴AP=,
∴位似中心点P的坐标是(,4),
综上所述,位似中心点的坐标是(0,0)或(,4),
故答案为:(0,0)或(,4).
14.(2021秋 揭西县期末)在平面直角坐标系中,△ABC中点A的坐标是(2,3),以原点O为位似中心把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,则点A的对应点A′的坐标为 (6,9)或(﹣6,﹣9) .
【解析】解:以原点O为位似中心,把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,
则点A(2,3)的对应点A′的坐标为(6,9)或(﹣6,﹣9).
故答案为:(6,9)或(﹣6,﹣9).
15.(2021秋 晋江市期中)五边形ABCDE位似于五边形A'B'C'D'E',它们的面积比为4:9,已知位似中心O到A点的距离为6,那么O到A'的距离为 9 .
【解析】解:∵五边形ABCDE和五边形A′B′C′D′E′是位似图形,它们的面积比为4:9,
∴它们的相似比为2:3,
∵位似中心O到A的距离为6,
∴O到A′的距离是6×=9,
故答案为:9.
16.(2021秋 新乡期末)如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,且△ABC和△A'B'C的周长之比为1:2,点C的坐标为(﹣1,0),若点B的对应点B'的横坐标为5,则点B的横坐标为 ﹣4 .
【解析】解:过点B作BE⊥x作于E,过点B′作B′F⊥x轴于F,
则BE∥B′F,
∴△BCE∽△B′CF,
∴=,
∵点C的坐标为(﹣1,0),点B'的横坐标为5,
∴CF=6,
∵△ABC和△A'B'C的周长之比为1:2,
∴△ABC和△A'B'C的相似比为1:2,即=,
∴=,
解得:EC=3,
∴点B的横坐标为﹣4,
故答案为:﹣4.
三.解答题
17.(2020秋 六盘水期末)在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(2,0),B(2,2),C(0,4).
(1)请画出四边形OABC关于y轴对称的四边形OEDC;
(2)以原点O为位似中心,请画出一个五边形A1B1C1D1E1与五边形ABCDE位似,且相似比是2:1.
【解析】解:(1)如图所示,四边形OEDC即为所求;
(2)如图所示,五边形A1B1C1D1E1即为所求(或五边形A2B2C2D2E2).
18.(2021秋 泉州期末)如图,在边长均为1的正方形网格中,△ABC的顶点均在格点上,O为直角坐标系的原点,△ABC三个顶点坐标分别为A(1,2)、B(0,1)、C(2,0).
(1)以O为位似中心,将△ABC放大为△A1B1C1,使得△A1B1C1与△ABC的相似比为2:1,请在网格中画出△A1B1C1(其中A1在第三象限内);
(2)直接写出(1)中点A1、B1、C1的坐标.
【解析】解:(1)如图,ΔA1B1C1为所作;
(2)A1(﹣2,﹣4),B1(0,﹣2),C1(﹣4,0).
19.(2021秋 新都区期末)如图,在边长为1的小正方形网格中.
(1)△ABC向右平移6个单位长度,再向上平移5个单位长度后得到△A1B1C1,请在网格中画出△A1B1C1,其中B1的坐标为 (11,6) ;
(2)以点A为位似中心,将△ABC放大为原来的2倍,得到△AB2C2,请在网格中画出△AB2C2;
(3)连接AB1,B1B2,则△AB1B2的面积为 20 .
【解析】解:(1)如图,△A1B1C1即为所求;
则B1(11,6);
故答案为:(11,6);
(2)如图,△AB2C2即为所求;
(3)△AB1B2的面积为:×8×5=20,
故答案为:20.
20.(2021秋 涡阳县期末)如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出△ABC关于x轴对称的△A'B'C';
(2)以坐标原点为位似中心在图中的网格中作出△A'B'C'的位似图形△A″B″C″,使△A'B'C'与△A″B″C″的位似比为1:2;
(3)若△ABC的面积为3.5平方单位,求出△A″B″C″的面积.
【解析】解:(1)如图,△A'B'C'即为所求;
(2)如图,△A″B″C″为所作;
(3)∵△A'B'C'∽△A″B″C″且位似比为1:2,△ABC的面积为3.5平方单位,
∴△A″B″C″的面积=4×3.5=14(平方单位).
21.(2021秋 振兴区校级月考)如图,在平面直角坐标系中,五边形A'B'C'D'E'是五边形ABCDE的位似图形,但图形并不完整.已知A点坐标(2,5),A′点坐标(2,3).
(1)请在图中标注位似中心P,并直接写出P点坐标 (2,1) ;
(2)请把两个五边形补充完整;
(3)请写出五边形A'B'C'D'E'与五边形ABCDE的位似比 .
【解析】解:(1)如图,位似中心P点的坐标(2,1).
故答案为:(2,1).
(2)五边形如图所示;
(3)位似比.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下 27.3位似同步练习
一.选择题
1.(2021秋 运城期末)如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,若OA:OA'=1:2,则△ABC与△A'B'C'的周长比为( )
A.1:4 B.1:3 C.1:2 D.1:9
2.(2021秋 南召县期末)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的面积的比是( )
A.1:2 B.1:3 C.1:9 D.9:1
3.(2021秋 瑞安市期末)如图,△ABC与△DEF是位似图形,O为位似中心,位似比为2:3.若AB=4,则DE的长为( )
A.6 B.8 C.9 D.10
4.(2021秋 永定区期末)如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形 B.点A是两个三角形的位似中心
C.AC:AB是相似比 D.点B与点D、点C与点E是对应位似点
5.(2021秋 邵东市期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
6.(2021秋 道县期末)下列说法正确的是( )
A.相似图形一定是位似图形 B.一条线段的黄金分割点只有一个
C.两个边数相同的正多边形是相似图形
D.相似三角形对应角的平分线的比等于对应边上高的比的平方
7.(2021秋 九龙坡区校级期末)如图,四边形ABCD和四边形A1B1C1D1是以点O为位似中心的位似图形,若OA:OA1=:2,则四边形ABCD与四边形A1B1C1D1的面积比为( )
A. B.3:4 C.3:2 D.9:4
8.(2021秋 仁寿县期末)点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法中错误的是( )
A.EF=BC B.EF与AD互相平分 C.△AFE是△ABC的位似图形 D.
9.(2021秋 太原期末)如图,在平面直角坐标系中,四边形ABCD与四边形A'B'C'D'是位似图形.位似中心到点D和点D'的距离的比值是( )
A.2 B. C. D.
二.填空题
10.(2021秋 市中区期末)如田,△ABC与△A′B′C′是位似图形,O为位似中心,若△ABC与△A′B′C′的面积之比为1:4,则CO:C′O的值为 .
11.(2021秋 肇东市期末)如图A'B'∥AB,B'C'∥BC,且OA':A'A=4:3,则△ABC与△A'B'C'是位似图形,△ABC与△A'B'C'的位似比为 .
12.(2021秋 曲阳县期中)如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为 .
13.(2021秋 大东区期末)线段AB、CD在平面直角坐标系中的网格位置.如图所示,O为坐标原点,A、B、C、D均在格点上,线段AB、CD是位似图形,位似中心的坐标是 .
14.(2021秋 揭西县期末)在平面直角坐标系中,△ABC中点A的坐标是(2,3),以原点O为位似中心把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,则点A的对应点A′的坐标为 .
15.(2021秋 晋江市期中)五边形ABCDE位似于五边形A'B'C'D'E',它们的面积比为4:9,已知位似中心O到A点的距离为6,那么O到A'的距离为 .
16.(2021秋 新乡期末)如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,且△ABC和△A'B'C的周长之比为1:2,点C的坐标为(﹣1,0),若点B的对应点B'的横坐标为5,则点B的横坐标为 .
三.解答题
17.(2020秋 六盘水期末)在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(2,0),B(2,2),C(0,4).
(1)请画出四边形OABC关于y轴对称的四边形OEDC;
(2)以原点O为位似中心,请画出一个五边形A1B1C1D1E1与五边形ABCDE位似,且相似比是2:1.
18.(2021秋 泉州期末)如图,在边长均为1的正方形网格中,△ABC的顶点均在格点上,O为直角坐标系的原点,△ABC三个顶点坐标分别为A(1,2)、B(0,1)、C(2,0).
(1)以O为位似中心,将△ABC放大为△A1B1C1,使得△A1B1C1与△ABC的相似比为2:1,请在网格中画出△A1B1C1(其中A1在第三象限内);
(2)直接写出(1)中点A1、B1、C1的坐标.
19.(2021秋 新都区期末)如图,在边长为1的小正方形网格中.
(1)△ABC向右平移6个单位长度,再向上平移5个单位长度后得到△A1B1C1,请在网格中画出△A1B1C1,其中B1的坐标为 ;
(2)以点A为位似中心,将△ABC放大为原来的2倍,得到△AB2C2,请在网格中画出△AB2C2;
(3)连接AB1,B1B2,则△AB1B2的面积为 .
20.(2021秋 涡阳县期末)如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出△ABC关于x轴对称的△A'B'C';
(2)以坐标原点为位似中心在图中的网格中作出△A'B'C'的位似图形△A″B″C″,使△A'B'C'与△A″B″C″的位似比为1:2;
(3)若△ABC的面积为3.5平方单位,求出△A″B″C″的面积.
21.(2021秋 振兴区校级月考)如图,在平面直角坐标系中,五边形A'B'C'D'E'是五边形ABCDE的位似图形,但图形并不完整.已知A点坐标(2,5),A′点坐标(2,3).
(1)请在图中标注位似中心P,并直接写出P点坐标 ;
(2)请把两个五边形补充完整;
(3)请写出五边形A'B'C'D'E'与五边形ABCDE的位似比 .
答案与解析
一.选择题
1.(2021秋 运城期末)如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,若OA:OA'=1:2,则△ABC与△A'B'C'的周长比为( )
A.1:4 B.1:3 C.1:2 D.1:9
【解析】解:∵OA:OA'=1:2,
∴AC:A′C′=1:2,
∴△ABC与△A′B′C′的相似比是1:2,
∴△ABC与△A′B′C′的周长比为1:2,
故选:C.
2.(2021秋 南召县期末)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的面积的比是( )
A.1:2 B.1:3 C.1:9 D.9:1
【解析】解:∵B(0,1),D(0,3),
∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
∴△OAB与△OCD的面积的比是1:9.
故选:C.
3.(2021秋 瑞安市期末)如图,△ABC与△DEF是位似图形,O为位似中心,位似比为2:3.若AB=4,则DE的长为( )
A.6 B.8 C.9 D.10
【解析】解:∵△ABC与△DEF是位似图形,位似比为2:3,
∴AB:DE=2:3.
∵AB=4,
∴DE=6.
故选:A.
4.(2021秋 永定区期末)如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形 B.点A是两个三角形的位似中心
C.AC:AB是相似比 D.点B与点D、点C与点E是对应位似点
【解析】解:A、两个三角形是位似图形,本选项说法正确,不符合题意;
B、点A是两个三角形的位似中心,本选项说法正确,不符合题意;
C、AC:AE是相似比,故本选项说法不正确,符合题意;
D、点B与点D、点C与点E是对应位似点,本选项说法正确,不符合题意;
故选:C.
5.(2021秋 邵东市期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
【解析】解:∵以原点O为位似中心,相似比为,把△EFO缩小,点E(﹣4,2),
∴点E的对应点E′的坐标是(﹣4×,2×)或(﹣4×(﹣),2×(﹣)),即(﹣2,1)或(2,﹣1),
故选:D.
6.(2021秋 道县期末)下列说法正确的是( )
A.相似图形一定是位似图形 B.一条线段的黄金分割点只有一个
C.两个边数相同的正多边形是相似图形
D.相似三角形对应角的平分线的比等于对应边上高的比的平方
【解析】解:A、位似图形一定是相似图形,但相似图形不一定是位似图形,本选项说法错误,不符合题意;
B、一条线段的黄金分割点有两个,本选项说法错误,不符合题意;
C、两个边数相同的正多边形是相似图形,本选项说法正确,符合题意;
D、相似三角形对应角的平分线的比等于对应边上高的比,本选项说法错误,不符合题意;
故选:C.
7.(2021秋 九龙坡区校级期末)如图,四边形ABCD和四边形A1B1C1D1是以点O为位似中心的位似图形,若OA:OA1=:2,则四边形ABCD与四边形A1B1C1D1的面积比为( )
A. B.3:4 C.3:2 D.9:4
【解析】解:∵四边形ABCD和四边形A1B1C1D1是以点O为位似中心的位似图形,OA:OA1=:2,
∴四边形ABCD和四边形A1B1C1D1的位似比为:2,
∴四边形ABCD与四边形A1B1C1D1的面积比3:4,
故选:B.
8.(2021秋 仁寿县期末)点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法中错误的是( )
A.EF=BC B.EF与AD互相平分 C.△AFE是△ABC的位似图形 D.
【解析】解:A、∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴EF=BC,本选项说法正确,不符合题意;
B、∵点D、E、F分别是△ABC各边的中点,
∴EF∥BC,ED∥AC,
∴四边形AEDF为平行四边形,
∴EF与AD互相平分,本选项说法正确,不符合题意;
C、∵EF∥BC,
∴△AEF∽△ABC,
∵△AFE和△ABC对应点的连线都经过同一点、对应边平行,
∴△AFE是△ABC的位似图形,本选项说法正确,不符合题意;
D、∵ED∥AC,
∴△BDE∽△BCA,
∴=,故本选项说法错误,符合题意;
故选:D.
9.(2021秋 太原期末)如图,在平面直角坐标系中,四边形ABCD与四边形A'B'C'D'是位似图形.位似中心到点D和点D'的距离的比值是( )
A.2 B. C. D.
【解析】解:如图所示:点P即为位似中心,位似中心到点D和点D'的距离的比值是:PD:PD′=2:1=2.
故选:A.
二.填空题
10.(2021秋 市中区期末)如田,△ABC与△A′B′C′是位似图形,O为位似中心,若△ABC与△A′B′C′的面积之比为1:4,则CO:C′O的值为 1:2 .
【解析】解:如图,△ABC与△A′B′C′是位似图形,O是位似中心,
∵△ABC与△A′B′C′的面积之比为1:4,
∴△ABC与△A′B′C′的相似比为1:2.
∵△ABC与△A′B′C′是位似图形,
∴△BCO∽△B′C′O′.
∴CO:C′O=BC:B′C′=1:2.
故答案为:1:2.
11.(2021秋 肇东市期末)如图A'B'∥AB,B'C'∥BC,且OA':A'A=4:3,则△ABC与△A'B'C'是位似图形,△ABC与△A'B'C'的位似比为 7:4 .
【解析】解:∵OA':A'A=4:3,
∴OA:OA′=7:4,
∵△ABC与△A'B'C'是位似图形,
∴A′B′∥AB,
∴△OAB∽△OA′B′,
∴==,
∴△ABC与△A'B'C'的位似比=7:4,
故答案为:7:4.
12.(2021秋 曲阳县期中)如图,△ABC与△DEF是位似图形,位似中心为O,OA:AD=3:4,S△ABC=9,则△DEF的面积为 49 .
【解析】解:∵OA:AD=3:4,
∴OA:OD=3:7,
∵△ABC与△DEF是位似图形,
∴AB∥DE,
∴△OAB∽△ODE,
∴==,
∴=()2=,
∵S△ABC=9,
∴△DEF的面积为49,
故答案为:49.
13.(2021秋 大东区期末)线段AB、CD在平面直角坐标系中的网格位置.如图所示,O为坐标原点,A、B、C、D均在格点上,线段AB、CD是位似图形,位似中心的坐标是 (0,0)或(,4) .
【解析】解:当点A和点C为对应点,点B和点D为对应点时,延长CA、BD交于点O,
则位似中心的坐标是(0,0),
当点A和点D为对应点,点B和点C为对应点时,连接AD、BC交于点P,
则点P为位似中心,
∵线段AB、CD是位似图形,
∴AB∥CD,
∴△PAB∽△PDC,
∴===,即=,
∴AP=,
∴位似中心点P的坐标是(,4),
综上所述,位似中心点的坐标是(0,0)或(,4),
故答案为:(0,0)或(,4).
14.(2021秋 揭西县期末)在平面直角坐标系中,△ABC中点A的坐标是(2,3),以原点O为位似中心把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,则点A的对应点A′的坐标为 (6,9)或(﹣6,﹣9) .
【解析】解:以原点O为位似中心,把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,
则点A(2,3)的对应点A′的坐标为(6,9)或(﹣6,﹣9).
故答案为:(6,9)或(﹣6,﹣9).
15.(2021秋 晋江市期中)五边形ABCDE位似于五边形A'B'C'D'E',它们的面积比为4:9,已知位似中心O到A点的距离为6,那么O到A'的距离为 9 .
【解析】解:∵五边形ABCDE和五边形A′B′C′D′E′是位似图形,它们的面积比为4:9,
∴它们的相似比为2:3,
∵位似中心O到A的距离为6,
∴O到A′的距离是6×=9,
故答案为:9.
16.(2021秋 新乡期末)如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,且△ABC和△A'B'C的周长之比为1:2,点C的坐标为(﹣1,0),若点B的对应点B'的横坐标为5,则点B的横坐标为 ﹣4 .
【解析】解:过点B作BE⊥x作于E,过点B′作B′F⊥x轴于F,
则BE∥B′F,
∴△BCE∽△B′CF,
∴=,
∵点C的坐标为(﹣1,0),点B'的横坐标为5,
∴CF=6,
∵△ABC和△A'B'C的周长之比为1:2,
∴△ABC和△A'B'C的相似比为1:2,即=,
∴=,
解得:EC=3,
∴点B的横坐标为﹣4,
故答案为:﹣4.
三.解答题
17.(2020秋 六盘水期末)在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(2,0),B(2,2),C(0,4).
(1)请画出四边形OABC关于y轴对称的四边形OEDC;
(2)以原点O为位似中心,请画出一个五边形A1B1C1D1E1与五边形ABCDE位似,且相似比是2:1.
【解析】解:(1)如图所示,四边形OEDC即为所求;
(2)如图所示,五边形A1B1C1D1E1即为所求(或五边形A2B2C2D2E2).
18.(2021秋 泉州期末)如图,在边长均为1的正方形网格中,△ABC的顶点均在格点上,O为直角坐标系的原点,△ABC三个顶点坐标分别为A(1,2)、B(0,1)、C(2,0).
(1)以O为位似中心,将△ABC放大为△A1B1C1,使得△A1B1C1与△ABC的相似比为2:1,请在网格中画出△A1B1C1(其中A1在第三象限内);
(2)直接写出(1)中点A1、B1、C1的坐标.
【解析】解:(1)如图,ΔA1B1C1为所作;
(2)A1(﹣2,﹣4),B1(0,﹣2),C1(﹣4,0).
19.(2021秋 新都区期末)如图,在边长为1的小正方形网格中.
(1)△ABC向右平移6个单位长度,再向上平移5个单位长度后得到△A1B1C1,请在网格中画出△A1B1C1,其中B1的坐标为 (11,6) ;
(2)以点A为位似中心,将△ABC放大为原来的2倍,得到△AB2C2,请在网格中画出△AB2C2;
(3)连接AB1,B1B2,则△AB1B2的面积为 20 .
【解析】解:(1)如图,△A1B1C1即为所求;
则B1(11,6);
故答案为:(11,6);
(2)如图,△AB2C2即为所求;
(3)△AB1B2的面积为:×8×5=20,
故答案为:20.
20.(2021秋 涡阳县期末)如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出△ABC关于x轴对称的△A'B'C';
(2)以坐标原点为位似中心在图中的网格中作出△A'B'C'的位似图形△A″B″C″,使△A'B'C'与△A″B″C″的位似比为1:2;
(3)若△ABC的面积为3.5平方单位,求出△A″B″C″的面积.
【解析】解:(1)如图,△A'B'C'即为所求;
(2)如图,△A″B″C″为所作;
(3)∵△A'B'C'∽△A″B″C″且位似比为1:2,△ABC的面积为3.5平方单位,
∴△A″B″C″的面积=4×3.5=14(平方单位).
21.(2021秋 振兴区校级月考)如图,在平面直角坐标系中,五边形A'B'C'D'E'是五边形ABCDE的位似图形,但图形并不完整.已知A点坐标(2,5),A′点坐标(2,3).
(1)请在图中标注位似中心P,并直接写出P点坐标 (2,1) ;
(2)请把两个五边形补充完整;
(3)请写出五边形A'B'C'D'E'与五边形ABCDE的位似比 .
【解析】解:(1)如图,位似中心P点的坐标(2,1).
故答案为:(2,1).
(2)五边形如图所示;
(3)位似比.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
